14. Теорема об изменении кинетической энергии механической системы [1,2,4,5]
Изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил:
 ; (14.1)
; (14.1)
это уравнение выражает теорему об изменении кинетической энергии в интегральной форме.
Производная по времени от кинетической энергии механической системы системы равно сумме мощностей от внешних и внутренних нагрузок.
 ; (14.2)
; (14.2)
равенство (14.2) выражает теорему об изменении кинетической энергии в дифференциальной форме.
Если в задаче требуется определить линейную или угловую скорость то пользуются теоремой об изменении кинетической энергии в интегральной форме. А если требуется определить линейное или угловое ускорение тогда для решения задачи применяют теорему об изменении кинетической энергии в дифференциальной форме.
Определение кинетическая энергия зависит от вида движения, которое совершает тело, входящее в механическую систему, поэтому различают три вида:
1) Поступательное движение,
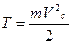 (14.3)
(14.3)
где m - масса тела, V – скорость центра масс
2) Вращательное движение,
 (14.4)
(14.4)
где I – момент инерции тела относительно оси вращения.
Для круглого сечения:
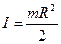
 , если задаётся радиус тела
, если задаётся радиус тела  , если задан радиус инерции тела
, если задан радиус инерции тела  , m – масса тела.
, m – масса тела.
3) Плоскопараллельное движение,

 +
+ 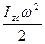 , (14.4)
, (14.4)
где  - скорость центра масс тела,
- скорость центра масс тела,  - момент инерции относительно оси Z, проходящий через центр масс С.
- момент инерции относительно оси Z, проходящий через центр масс С.
Рассмотрим определение работы от внешних нагрузок:
1. Работа от силы тяжести:
 ,
,
где m – масса тела, g-ускорение свободного падения, h-вертикальное перемещение центра масс (или центра тяжести).
Работа считается положительной если направление движения совпадает с направлением силы тяжести или её составляющей направление движения (рис.14.1).

Рис.14.1
2.Работа от вращательного момента:
 , (14.5)
, (14.5)
Если направление вращательного момента совпадает с движением тела, то такая работа считается положительной.
Определение угла поворота:
 , (14.6)
, (14.6)
где S – длинна участка пути за рассматриваемый период времени, R – радиус тела,  - угол поворота.
- угол поворота.
Рассмотрим частный случай, когда работа равна нулю:
1. А(F) = 0, если  (S – перемещение)
(S – перемещение) 
Рис. 14.2
2. А(F) = 0, если точка приложения силы  - неподвижная.
- неподвижная. 
Рис. 14.3
Определим мощность:
1. От силы F:
N(F)=  FV, (14.7)
FV, (14.7)
где V – скорость точки приложения силы.
2. От вращательного момента M:
N(M)=  M
M  (14.8)
(14.8)
где  - угловая скорость тела.
- угловая скорость тела.
Пример 14.1
 Ступенчатый шкив 1, имеющий массу
Ступенчатый шкив 1, имеющий массу  и радиус инерции относительно оси вращения
и радиус инерции относительно оси вращения  , обмотан гибкими нерастяжимыми нитями. К нити, сходящей со ступени радиуса
, обмотан гибкими нерастяжимыми нитями. К нити, сходящей со ступени радиуса  прикреплен груз 2 массы
прикреплен груз 2 массы  . К нити, сходящей со ступени радиуса
. К нити, сходящей со ступени радиуса  , шарнирно прикреплен цилиндр 3 в точке
, шарнирно прикреплен цилиндр 3 в точке  , лежащей на его оси. Этот цилиндр также обмотан нитью, конец которой закреплен в точке А. Участки
, лежащей на его оси. Этот цилиндр также обмотан нитью, конец которой закреплен в точке А. Участки 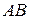 и
и  параллельны. Радиус цилиндра равен
параллельны. Радиус цилиндра равен  , а его масса -
, а его масса -  и равномерно распределена по его объему. Массы и радиусы удовлетворяют условию
и равномерно распределена по его объему. Массы и радиусы удовлетворяют условию  . Пренебрегая трением в шарнирах, определить угловую скорость
. Пренебрегая трением в шарнирах, определить угловую скорость  ступенчатого шкива в функции угла
ступенчатого шкива в функции угла  его поворота, его угловое ускорение
его поворота, его угловое ускорение 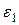 , натяжения нитей
, натяжения нитей  ,
,  ,
, 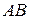 и реакцию оси
и реакцию оси  . В начальный момент система неподвижна (рис.14.4).
. В начальный момент система неподвижна (рис.14.4).
Решение:
Кинетическая энергия ступенчатого вала, вращающегося вокруг неподвижной оси:
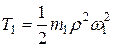 .
.
Кинетическая энергия груза 2, совершающего поступательное движение:
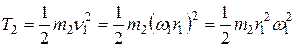 .
.
Кинетическая энергия цилиндра, совершающего плоскопараллельное движение:
 .
.

Рис.14.4
Мгновенный центр скоростей сечения цилиндра плоскостью чертежа находится в точке В (так как скорость участка нити АВ равна нулю).
Поэтому  . Момент инерции цилиндра
. Момент инерции цилиндра  . Подставив эти выражения в формулу для
. Подставив эти выражения в формулу для  , получим:
, получим:
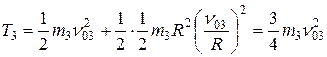 .
.
Учитывая, что  , окончательно
, окончательно
 .
.
Кинетическая энергия системы:
 .
.
При повороте ступенчатого шкива на угол  груз
груз  опускается на величину
опускается на величину  , а ось цилиндра поднимается на
, а ось цилиндра поднимается на  . Сумма работ сил тяжести:
. Сумма работ сил тяжести:
 .
.
Другие силы, приложенные в данной системе, работы не совершают.
Так как в начальный момент система неподвижна, то по теореме об изменении кинетической энергии:
 .
.
Это равенство и определяет зависимость  от
от  .
.
Чтобы найти угловое ускорение шкива 1, дифференцируем левую и правую части этого равенства по времени:
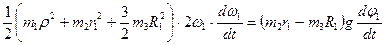 .
.
Так как  ,
,  , то отсюда получаем:
, то отсюда получаем:
 .
.
 Чтобы определить натяжение
Чтобы определить натяжение  нити
нити  , напишем уравнение второго закона Ньютона для груза 2, к которому приложены силы
, напишем уравнение второго закона Ньютона для груза 2, к которому приложены силы  и
и  (рис. 14.5):
(рис. 14.5):
 ,
,
где  - ускорение груза.
- ускорение груза.
Отсюда:

 .
.
Для определения натяжения  нити
нити  применим к ступенчатому шкиву дифференциальное уравнение вращения твердого тела вокруг неподвижной оси. К шкиву приложены силы
применим к ступенчатому шкиву дифференциальное уравнение вращения твердого тела вокруг неподвижной оси. К шкиву приложены силы  ,
,  ,
,  ,
,  (рис. 14.6). Поэтому
(рис. 14.6). Поэтому
 .
.
Так как  , то отсюда
, то отсюда
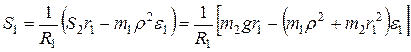 .
.
Для определения реакции  применим к шкиву теорему о движении центра масс:
применим к шкиву теорему о движении центра масс:
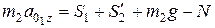 .
.
Так как  , то
, то

 .
.
Наконец, для определения натяжения  нити АВ применим теорему о движении центра масс к цилиндру 3, на который действуют внешние силы
нити АВ применим теорему о движении центра масс к цилиндру 3, на который действуют внешние силы  ,
,  ,
,  (рис. 14.7):
(рис. 14.7):
 .
.
Так как  , то отсюда:
, то отсюда:

Подставив сюда выражение 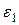 , получим
, получим 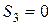 .
.
Пример 14.2
Дано: P,  , Q, S- перемещение 1 тела;
, Q, S- перемещение 1 тела; 

Определить: скорость груза 1(Рис.14.8).

Рис.14.8
Решение:
1. Определим скорость груза, пользуясь теоремой об изменении кинетической энергии в интегральной форме:

 ,
,

(действие внутренних нагрузок не учитываем, т.к. элементарная работа действующих на точку внутренних сил равна нулю по свойству внутренних сил системы)
2. Определим кинетическую энергию всей механической системы.
Кинетическая энергия системы равна сумме кинетических энергий тел, входящих в систему.
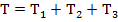
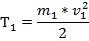
(тело1 совершает поступательное движение)

(тело 2 совершает вращательное движение)


Выразим  через
через  .
.

 ;
;

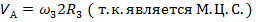
 ;
;

 ;
; 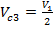 ;
;
 =
= 

Выполним подстановку и определим кинетическую энергию системы:

3. Определим работы внешних сил, действующих на механическую систему.


A (P) =P*S
4. Приравняем левую и правую части уравнений согласно:
 = P*S
= P*S
 .
.
Пример 14.3
Определить ускорение центра катка 1, если его вес P, он имеет круглое сечение радиусом R. Вес барабана, приводящего механическую систему в движение Q, его радиус r, вращательный момент M, угол наклона плоскости, на которой находится каток 1- α (рис.14.9).
Решение:
1. Применим теорему об изменении кинетической энергии механической системы в дифференциальном виде:


2. Определим кинетическую энергию механической системы:

где  - кинетическая энергия катка, совершающего плоскопараллельное движение;
- кинетическая энергия катка, совершающего плоскопараллельное движение;
 - кинетическая энергия блока, совершающего вращательное движение.
- кинетическая энергия блока, совершающего вращательное движение.
 ,
, 

Рис.14.9
Моменты инерции тел:
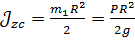 ,
,
где  =
=  .
.
 ,
,
где  .
.
Выразим все кинетические параметры через величину одноименной искомой величине  :
:
 ,
,  .
.
Так как для катка 1 в точке касания его с неподвижной плоскостью находится мгновенный центр скоростей, то имеем соотношение между скоростями:
 =
=  , т.е.
, т.е.  .
.
Тогда:
 .
.
Подставим все в уравнение и определим кинетическую энергию системы:

Найдем производную от последнего выражения:
 = (3P+4Q) *
= (3P+4Q) * 
где  =
= 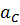 .
.
3. Определим мощность от внешних нагрузок, действующих на механическую систему:

N(Q)=0, так как точка приложения силы  неподвижная.
неподвижная.  ,
,
(отрицательная по знаку мощность, так как составляющая силы  противоположна направлению движения, чем направление вектора скорости катка).
противоположна направлению движения, чем направление вектора скорости катка).
 ,
,
(мощность по знаку положительная, так как направление вращательного момента, приложенного к блоку, совпадает с направлением вращения блока).
 .
.
Подставим все в исходное уравнение:
(3P+4Q) *  ,
,
 ,
,
 .
.
Пример 14.4
Условие: m1=8 кг, т2=0 кг, m3=5 кг, т4=0 кг, m5=6 кг, М=0,8 Н/м, 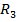 =0,3 м,
=0,3 м,  =0,1 м,
=0,1 м, 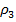 =0,2 м,
=0,2 м,  =0,2 м,
=0,2 м,  =0,2 м. Найти
=0,2 м. Найти  , схема механической системы приведена на рис.14.10
, схема механической системы приведена на рис.14.10

Рис.14.10
Решение:
Составим расчётную схему с указанием всех сил действующих на механическую систему (рус. 14.10) По теореме о изменении кинетической энергии системы:
 .
.
В начальный момент времени Т0= 0. Сумма внутренних сил

(по свойству внутренних сил).
Определим кинетическую энергию системы:
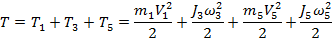 .
.
Выразим  и
и  через
через  (точка С - мгновенный центр скоростей):
(точка С - мгновенный центр скоростей):
 =
= 
 ;
;
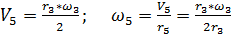 .
.
Определим моменты инерции:
 m3*
m3* 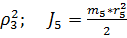 ..
..

Найдём сумму работ всех действующих сил при 
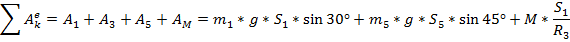
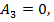 так как точка приложения силы неподвижна
так как точка приложения силы неподвижна


Подставляем полученные уравнения для кинетической энергии и суммы работ в формулу теоремы об изменении кинетической энергии:
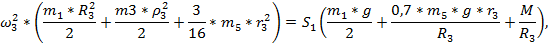
решая это уравнение относительно  получим:
получим:

Ответ: 
Пример 14.5
Механическая система (рис. 14.12) приводится в движение из состояния покоя под действием пары с моментом  или силы
или силы  . Масса тележки с грузом или одного груза 1
. Масса тележки с грузом или одного груза 1  задана в таблице; масса четырех колес тележки 2
задана в таблице; масса четырех колес тележки 2 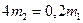 ;масса барабана с колесом 3
;масса барабана с колесом 3  ; масса колеса 4
; масса колеса 4  ; массой подвижного блока 2 пренебречь. Наружный радиус
; массой подвижного блока 2 пренебречь. Наружный радиус 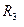 задан в таблице;
задан в таблице;  ;
; 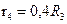 ;
; 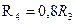 ; радиус инерции тела 3
; радиус инерции тела 3  . Колеса тележки 2 и колесо 4 считать сплошными цилиндрами, трос – невесомой, нерастяжимой нитью. Колеса тележки катятся по наклонной плоскости
. Колеса тележки 2 и колесо 4 считать сплошными цилиндрами, трос – невесомой, нерастяжимой нитью. Колеса тележки катятся по наклонной плоскости  без проскальзывания. При движении на барабан 3 действует момент сил сопротивления
без проскальзывания. При движении на барабан 3 действует момент сил сопротивления  .
.
Дано:  ,
,  ,
,  ,
,  ,
, 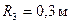 ,
, 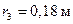 ,
,  ,
,  ,
,  ,
,  ,
, 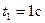 ,
, 
Определить: М, N для 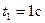 .
.
Решение:
1. Определение M. Применим теорему об изменении кинетической энергии неизменяемой системы в дифференциальной форме

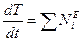
Изобразим действующие на систему внешние заданные силы 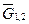 ,
,  ,
,  и моменты M и Mc. Кинетическая энергия системы
и моменты M и Mc. Кинетическая энергия системы

где  ,
,  ,
,
 ,
, 
Выразим  ,
,  ,
,  ,
,  через
через  ; так как точка К – мгновенный центр скоростей колеса 2, то
; так как точка К – мгновенный центр скоростей колеса 2, то 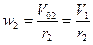 ;
;
Рис. 14.12
 ; так как
; так как  ; то отсюда
; то отсюда
 .
.
Моменты инерции тел 2,3,4 равны  ,
, 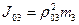 ,
,  .
.
Подставив все эти значения получим кинетическую энергию системы:
 .
.
Сумма мощностей внешних сил и моментов:
 ,
,
где  ,
,
 ,
,
 .
.
Подставив в исходное уравнение и взяв производную 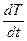 , получим:
, получим:  .
.
Отсюда, подставив числовые значения заданных величин, найден искомый момент: 
2. Определение  . Так как движение системы равноускоренное, то при
. Так как движение системы равноускоренное, то при  угловая скорость
угловая скорость  .
.
Следовательно:
 .
.