Задача Д-3.1. Механическая система (рис.17.4) приводится в движение из состояния покоя под действием пары с моментом  или силы
или силы  . Масса тележки с грузом или одного груза 1
. Масса тележки с грузом или одного груза 1  задана в таблице 1; масса четырех колес тележки 2
задана в таблице 1; масса четырех колес тележки 2 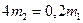 ;
;
масса барабана с колесом 3  ; масса колеса 4
; масса колеса 4  ; массой подвижного блока 2 пренебречь. Наружный радиус
; массой подвижного блока 2 пренебречь. Наружный радиус 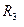 задан в таблице17.1;
задан в таблице17.1;  ;
; 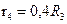 ;
; 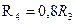 ; радиус инерции тела 3
; радиус инерции тела 3  . Колеса тележки 2 и колесо 4 считать сплошными цилиндрами, трос – невесомой, нерастяжимой нитью. Колеса тележки катятся по наклонной плоскости
. Колеса тележки 2 и колесо 4 считать сплошными цилиндрами, трос – невесомой, нерастяжимой нитью. Колеса тележки катятся по наклонной плоскости  без проскальзывания. При движении на барабан 3 действует момент сил сопротивления
без проскальзывания. При движении на барабан 3 действует момент сил сопротивления  .
.
. С помощью общего уравнения динамики определить зависимость М или Р от ускорения  .
.
Таблица 17.1
Исходные данные для задачи Д-3.1
| № условия |  , кг , кг
|  , м , м
| 
| 
|
| 0,1 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,33 0,37 0,48 0,45 0,29 0,32 0,31 0,39 | 0,5 0,4 0,35 0,3 0,3 0,25 0,25 0,2 0,32 0,41 0,26 0,28 0,29 0,25 0,24 0,27 |

Рис.17.4

Рис.17.4-продолжение
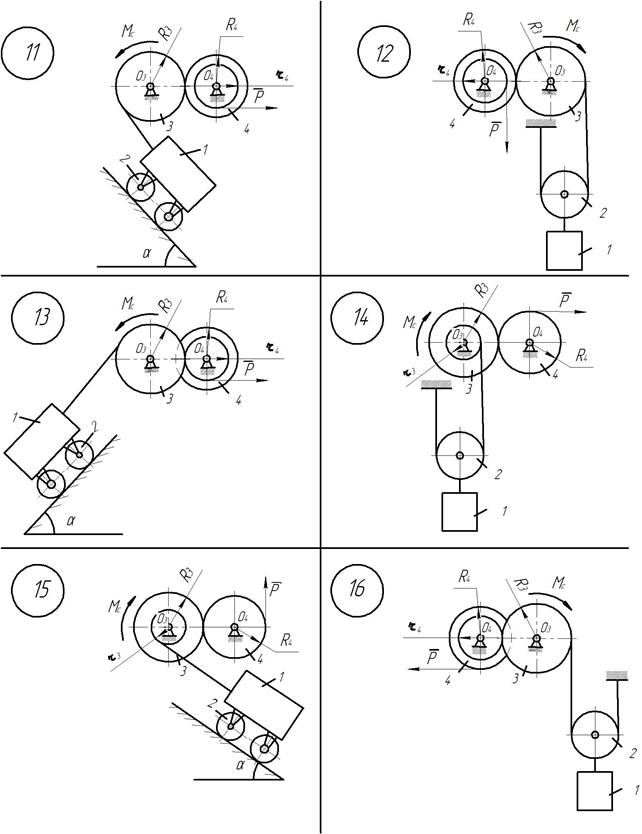
Рис.17.4-окончание
Задача Д 3.2. Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3 – 6, прикрепленных к этим нитям, и невесомого блока (рис. 17.5, табл. 17.2). Система движется в вертикально плоскости под действием сил тяжести и пары сил с моментом  , приложенной к одному из шкивов. Радиусы ступеней шкива 1 равны:
, приложенной к одному из шкивов. Радиусы ступеней шкива 1 равны: 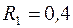 м,
м,  м, а шкива 2 -
м, а шкива 2 -  м,
м,  м; их радиусы инерции относительно осей вращения равны соответственно
м; их радиусы инерции относительно осей вращения равны соответственно  м и
м и  м.
м.
Пренебрегая трением, определить ускорение груза, имеющего больший вес; веса 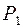 , …,
, …,  шкивов и грузов заданы в таблице в ньютонах. Грузы, веса которых равны нулю, на чертеже не изображать (шкивы 1, 2 изображать всегда как части системы).
шкивов и грузов заданы в таблице в ньютонах. Грузы, веса которых равны нулю, на чертеже не изображать (шкивы 1, 2 изображать всегда как части системы).
Указания. ЗадачаД 3.21 - на применение к изучению движения системы общего уравнения динамики (принципа Даламбера - Лагранжа). Учесть при этом, что для однородного тела, вращающегося вокруг своей оси симметрии (шкива), система сил инерции приводится к паре с моментом  , где
, где  - момент инерции тела относительно оси вращения,
- момент инерции тела относительно оси вращения,  - угловое ускорение тела; направление
- угловое ускорение тела; направление  противоположно направлению
противоположно направлению  .
.
Таблица 17.2
Исходные данные для задачи Д-3.2
| вариант | I | II | III | ||||
| 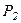
| 
| 
| 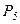
| 
|  ,
Н м ,
Н м
| |
| 0,94 | |||||||
| 1,25 | |||||||
| 0,68 | |||||||
| 1,85 | |||||||
| 1,24 |
Продолжение таблицы 17.2
| 0,93 | |||||||
| 1,85 | |||||||
| 0,65 | |||||||
| 0,94 | |||||||
| 1,28 | |||||||
| 1,23 | |||||||
| 0,95 | |||||||
| 0,85 | |||||||
| 1,45 | |||||||
| 1,25 | |||||||
| 1,85 | |||||||
| 1,95 | |||||||
| 1,55 |

 Рис.17.5
Рис.17.5
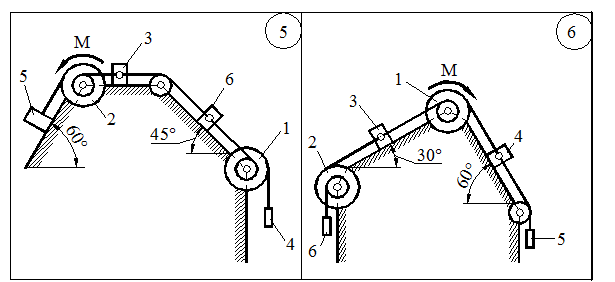


Рис. 17.5 – окончание
Практическое занятие 18
Применение уравнений Лагранжа второго рода к исследованию движения механической системы с одной степенью свободы
18. Уравнения Лагранжа [1,2,4,5,6]
.
Уравнения Лагранжа дают единый и притом достаточно простой метод решения задач динамики. Важное преимущество этих уравнений, состоит в том что их вид и число не зависят, ни от количества тел (или точек), входящих в рассматриваемую систему, ни от того, как эти тела движутся; определяется числом уравнений Лагранжа только числом степеней свободы системы. Кроме того, при идеальных связях в правые части уравнений (18.1) входят обобщенные активные силы и следовательно эти уравнения позволяют заранее исключить их рассмотрения все наперед известные реакции связей.
 (18.1)
(18.1)
Уравнения (18.1) представляют собой дифференциальные уравнения движения системы в обобщенных координатах или уравнениях Лагранжа. Число этих уравнений как видим равно числу степеней свободы системы.
Выбираем за обобщенную координату перемещение груза S1 и записываем уравнение Лагранжа:
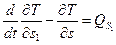 (18.2)
(18.2)
Обобщенная сила равна
 (18.3)
(18.3)
Пример 18.1
Сплошной однородный цилиндр 1 массой  кг и радиусом
кг и радиусом  м может вращаться без трения вокруг неподвижной горизонтальной оси
м может вращаться без трения вокруг неподвижной горизонтальной оси  . С цилиндром жестко скреплены тонкие однородны стержни 3 и 4 массой
. С цилиндром жестко скреплены тонкие однородны стержни 3 и 4 массой  и длиной
и длиной 
 каждый. В середине В стержня 4 к нему прикреплена нить, перекинутая через невесомый блок 2 и намотанная на цилиндр 5, одинаковый с цилиндром 1. При движение системы ось
каждый. В середине В стержня 4 к нему прикреплена нить, перекинутая через невесомый блок 2 и намотанная на цилиндр 5, одинаковый с цилиндром 1. При движение системы ось 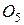 цилиндра 5 перемещается по вертикали. В точке Д к стержню 3 прикреплена пружина жесткостью
цилиндра 5 перемещается по вертикали. В точке Д к стержню 3 прикреплена пружина жесткостью  кН/м. В начальном положении системы стержень 3 и участок нити между стержнем и блоком расположены горизонтально, а стержень 4 и ось пружины – вертикально; пружина растянута на величину
кН/м. В начальном положении системы стержень 3 и участок нити между стержнем и блоком расположены горизонтально, а стержень 4 и ось пружины – вертикально; пружина растянута на величину  (рис. 18.1).
(рис. 18.1).
Начальные значения обобщенных координат  и
и  равны нулю, а обобщенных скоростей -
равны нулю, а обобщенных скоростей -  ,
, 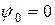 . Трением в осях
. Трением в осях  ,
, 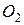 , массой пружины и нити пренебрегаем.
, массой пружины и нити пренебрегаем.
Используя уравнение Лагранжа II рода, найти кинематические уравнения движения системы при малых отклонениях цилиндра 1 от начального положения и определить круговую частоту и период колебания системы.
Решение.
Кинетическая энергия системы равна сумме кинетических энергий вращающегося цилиндра 1 с жестко присоединенными к нему стержнями и цилиндра 5, совершающего плоскопараллельное движение:
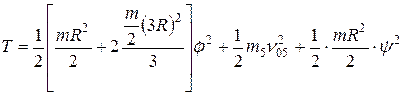 .
.
В этом выражении  - момент инерции цилиндра относительно его оси;
- момент инерции цилиндра относительно его оси;  - момент инерции стержня; в квадратных скобках – момент инерции цилиндра 1 с жестко присоединенными к нему стержнями.
- момент инерции стержня; в квадратных скобках – момент инерции цилиндра 1 с жестко присоединенными к нему стержнями.
Скорость 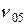 центра цилиндра 5 равна сумме скорости точки
центра цилиндра 5 равна сумме скорости точки  нити и скорости
нити и скорости 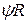 точки
точки 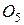 во вращательном движении вокруг полюса
во вращательном движении вокруг полюса  .
.
 Для определения
Для определения 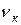 рассмотрим положение системы, при котором цилиндр 1 и стержни 3 и 4 отклонены от начального положения на угол
рассмотрим положение системы, при котором цилиндр 1 и стержни 3 и 4 отклонены от начального положения на угол  (рис. 18.2). Скорость точки
(рис. 18.2). Скорость точки  нити равна скорости точки Е, в которой участок нити ВЕ касается блока 2. Так как нить нерастяжима, то проекция скоростей точек В и Е на направление нити равны. Поэтому:
нити равна скорости точки Е, в которой участок нити ВЕ касается блока 2. Так как нить нерастяжима, то проекция скоростей точек В и Е на направление нити равны. Поэтому:
 .
.
Теперь воспользуемся малостью отклонений стержней от начального положения. Как известно, функция  и
и  можно разложить в ряды Маклорена:
можно разложить в ряды Маклорена:
 ;
;
 .
.
При «малых»  (до 0,1 радиана) значения
(до 0,1 радиана) значения  и
и  отличаются от первых членов соответствующих разложений менее чем на 0,5%. Поэтому можно принять
отличаются от первых членов соответствующих разложений менее чем на 0,5%. Поэтому можно принять  ,
,  . Так как при «малом»
. Так как при «малом»  угол
угол  также является «малым», то
также является «малым», то  . Поэтому в этом случае:
. Поэтому в этом случае:
 , тогда
, тогда  .
.
Подставляя 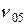 в ранее написанное выражение для Т, после простых преобразований приводим его к виду:
в ранее написанное выражение для Т, после простых преобразований приводим его к виду:
 .
.
Для нахождения обобщенных сил  и
и 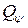 , соответствующих обобщенным координатам
, соответствующих обобщенным координатам  и
и  , вновь обратимся к рис. 18.2. Чтобы определить
, вновь обратимся к рис. 18.2. Чтобы определить  , дадим мысленно системе возможное перемещение, при котором обобщенная координата
, дадим мысленно системе возможное перемещение, при котором обобщенная координата  изменяется на бесконечно малую величину
изменяется на бесконечно малую величину 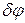 , а обобщенная координата
, а обобщенная координата  не изменяется. В этом случае точка В получит возможное перемещение
не изменяется. В этом случае точка В получит возможное перемещение 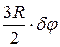 , направленное по вектору
, направленное по вектору  . Такие же по абсолютному значению перемещения при «малых»
. Такие же по абсолютному значению перемещения при «малых»  получат точки Е, G, К и
получат точки Е, G, К и 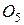 . Поэтому сила тяжести цилиндра 5 совершит работу
. Поэтому сила тяжести цилиндра 5 совершит работу  . Работа сил тяжести стержней и силы упругости
. Работа сил тяжести стержней и силы упругости  пружины равна произведению их момента относительно оси вращения
пружины равна произведению их момента относительно оси вращения  на угол поворота
на угол поворота 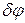 , т.е.
, т.е.
 .
.
Из рис. 1.2 видно (см.  ), что
), что
 .
.
При 
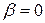 . Этот результат означает, что угол
. Этот результат означает, что угол 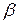 является малым более высокого порядка, чем
является малым более высокого порядка, чем  (имеет порядок квадрата
(имеет порядок квадрата  ), и по сравнению с
), и по сравнению с  им можно пренебречь. Тогда сумма работ всех задаваемых сил при повороте цилиндра 1 на угол
им можно пренебречь. Тогда сумма работ всех задаваемых сил при повороте цилиндра 1 на угол 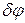 будет:
будет:
 .
.
Укорочение пружины, соответствующее положению цилиндра 1, повернутому из начального положения на угол  , равно разности
, равно разности 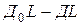 . Длина
. Длина  укоротившейся пружины равна
укоротившейся пружины равна
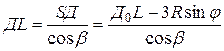 ,
,
или при «малых»  :
:
 .
.
Следовательно, укорочение пружины
 .
.
Так как в начальный момент пружина была растянута на величину  , то ее растяжение уменьшается и станет
, то ее растяжение уменьшается и станет  , а упругая сила будет
, а упругая сила будет  .
.
Обобщенна сила, соответствующая углу  :
:
 ,
,
или окончательно
 .
.
Для нахождения обобщенной силы 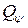 , соответствующей обобщенной координате
, соответствующей обобщенной координате  , нужно сообщить системе возможное перемещение, при котором
, нужно сообщить системе возможное перемещение, при котором  останется неизменным, а
останется неизменным, а  увеличивается на бесконечно малую величину
увеличивается на бесконечно малую величину  . В этом случае работу совершает только сила тяжести цилиндра 5:
. В этом случае работу совершает только сила тяжести цилиндра 5:  .
.
Обобщенная сила:
 .
.
Теперь составим уравнение Лагранжа:
 ,
,  .
.
Частные производные:
 ;
;  .
.
 ,
,  .
.
Уравнение Лагранжа будет иметь вид:
 ;
;
 .
.
Из второго уравнения после сокращения его на  :
:
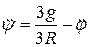 .
.
Подставив это выражение в первое уравнение, после простых преобразований получим:
 .
.
Обозначим:
 .
.
Величина:
 1/с
1/с
и представляет искомую круговую частоту колебаний.
Период колебаний:
 с.
с.
Общее решение дифференциального уравнения малых колебаний цилиндра:

есть функция:
 .
.
Для нахождения постоянных интегрирования 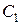 и
и  используем начальные условия: при
используем начальные условия: при  ,
, 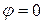 ,
,  (1/с).
(1/с).
Из первого условия следует  ; из второго условия, учитывая, что:
; из второго условия, учитывая, что:
 ,
,
получаем 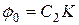 ;
;  . Поэтому окончательно:
. Поэтому окончательно:
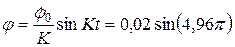 .
.
Для нахождения  интегрируем ранее полученное уравнение:
интегрируем ранее полученное уравнение:
 .
.
Имеем:
 .
.
Из начальных условий: при  ,
, 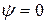 ,
,  следует
следует  ;
;  . Тогда:
. Тогда:
 .
.
Интегрируя еще раз, получаем:
 .
.
Из начальных условий: при  ,
, 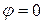 ,
,  следует
следует 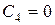 . Поэтому:
. Поэтому:
 .
.
После подстановки числовых значений:
 .
.
Пример 18.2
 Вывести кинематические уравнения движения системы, показанной на рис.18.3, пренебрегая массой пружины. Качение катка происходит без проскальзывания. Трением в оси
Вывести кинематические уравнения движения системы, показанной на рис.18.3, пренебрегая массой пружины. Качение катка происходит без проскальзывания. Трением в оси  пренебречь. Блок и каток – одинаковые цилиндры радиусом
пренебречь. Блок и каток – одинаковые цилиндры радиусом  м и массой
м и массой  кг, равномерно распределенной по их объему. Жесткость пружины
кг, равномерно распределенной по их объему. Жесткость пружины  Н/м.
Н/м.
Начальные значения обобщенных координат 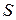 и
и  равны нулю; начальное удлинение пружины
равны нулю; начальное удлинение пружины  ; начальные значения обобщенных скоростей
; начальные значения обобщенных скоростей  м/с,
м/с,  .
.
Решение:
Кинетическая энергия системы:
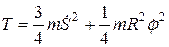 .
.
Обобщенные силы:
 ,
,  ,
,
где  - сила упругости пружины.
- сила упругости пружины.
Уравнение Лагранжа для рассмотренной системы:
 ;
; 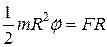 .
.
Сила упругости  зависит от деформации
зависит от деформации 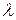 пружины, которая равна
пружины, которая равна  , где
, где  - начальное значение деформации. Обозначим
- начальное значение деформации. Обозначим  . Тогда
. Тогда  ;
;  . С другой стороны, дифференциальные уравнения движения системы можно представить в виде:
. С другой стороны, дифференциальные уравнения движения системы можно представить в виде:
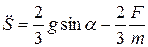 ;
;  .
.
Вычитая из первого уравнение второе, получаем
 ,
,
или
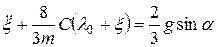 .
.
Подставляя заданное значение  , получим:
, получим:
 , где
, где 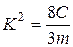 .
.
Решением этого дифференциального уравнения при начальных условиях: при  ,
, 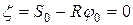 ,
, 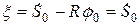 является функция:
является функция:  . Тогда
. Тогда  .
.
Дифференциальные уравнения движения системы принимают вид:
 ;
;
 .
.
Интегрируя эти уравнения при начальных условиях:  ,
, 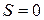 ,
,  ,
, 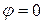 ,
, 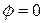 , получим:
, получим:
 ;
;
 ;
;
 ;
;
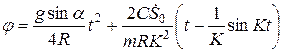 .
.
После подстановки численных значений получим:
 ;
;
 .
.
Пример 18.3
Дано:  ,
,  ,
,  ,
,  ,
, 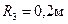 ,
,  ,
,  ,
, 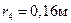 ,
,  ,
,  (рис.18.4)
(рис.18.4)
Решение:
Определим P с помощью уравнения Лагранжа 2-го рода. Выберем за обобщенную координату перемещение груза 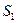 и запишем уравнение Лагранжа:
и запишем уравнение Лагранжа:
 .
.
Кинетическая энергия системы:
 .
.
Выразим  и
и  через
через  :
:
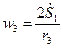 ,
, 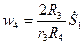

Рис.18.4
Подставив эти значения, а также  ,
, 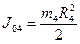 , определим кинетическую энергию системы:
, определим кинетическую энергию системы:
 .
.
Определим производные:
 ;
;  .
.
Для определения обобщенной силы, сообщим системе возможное перемещение при  . Обобщенная сила определяется с помощью выражения:
. Обобщенная сила определяется с помощью выражения:
 .
.
Подставив:
 ,
,
 .
.
Получим:
 .
.
Подставив полученные результаты в исходную формулу, получим:
 .
.
Отсюда определяем  :
:
 .
.
Это выражение совпадает с выражениями полученными при решении задачи другими способами.