Что будет, если вектор 
умножить на самого себя?
Или: 
Число 
называется скалярным квадратом вектора , и обозначатся как 
.
Таким образом, скалярный квадрат вектора равен квадрату длины данного вектора:
Из данного равенства можно получить формулу для вычисления длины вектора:
С войства скалярного произведения.
Для произвольных векторов 
и любого числа 
справедливы следующие свойства:
1) 
– переместительный или коммутативный закон скалярного произведения.
2) 
– распределительный или дистрибутивный закон скалярного произведения. Попросту, можно раскрывать скобки.
3) 
– сочетательный или ассоциативный закон скалярного произведения. Константу можно вынести из скалярного произведения.
Пример
Найти скалярное произведение векторов 
и 
, если известно, что 
.
Решение:
(1) Подставляем выражения векторов 
.
(2) Раскрываем скобки по правилу умножения многочленов. Раскрыть скобки нам позволяет дистрибутивное свойство скалярного произведения.
(3) В первом и последнем слагаемом компактно записываем скалярные квадраты векторов: 
. Во втором слагаемом используем перестановочность скалярного произведения: 
.
(4) Приводим подобные слагаемые: 
.
(5) В первом слагаемом используем формулу скалярного квадрата , о которой не так давно упоминалось. В последнем слагаемом, соответственно, работает та же штука: 
. Второе слагаемое раскладываем по стандартной формуле 
.
(6) Подставляем данные условия 
, и ВНИМАТЕЛЬНО проводим окончательные вычисления.
Ответ: 
Пример
Найти длину вектора 
, если 
.
Решение:
(1) Поставляем выражение вектора 
.
(2) Используем формулу длины: 
, при этом в качестве вектора «вэ» у нас выступает целое выражение 
.
|
|
(3) Используем школьную формулу квадрата суммы 
.
(4) Дальнейшее аналогично действиям из двух предыдущих задач.
Ответ: 
Угол между векторами
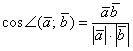
Если известны длины двух векторов и их скалярное произведение, то можно вычислить косинус угла между данными векторами, а, следовательно, и сам угол.
.
Пример
Найти угол между векторами и 
, если известно, что 
.
Решение: Используем формулу:
На заключительном этапе вычислений использован технический приём – устранение иррациональности в знаменателе. В целях устранения иррациональности я домножил числитель и знаменатель на 
.
Итак, если 
, то:
Ответ: 
Не забываем указывать размерность – радианы и градусы.
Пример
Даны 
– длины векторов , и угол между ними 
. Найти угол между векторами 
, 
.
Алгоритм решения:
1) По условию требуется найти угол между векторами и 
, поэтому нужно использовать формулу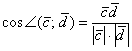 
.
2) Находим скалярное произведение 
.
3) Находим длину вектора и длину вектора .
4) Нам известно число 
, а значит, легко найти и сам угол: 
Сделайте самостоятельно и сравните с решением.
Решение: Найдём скалярное произведение:
Найдём длину вектора :
Найдём длину вектора :
Таким образом:
Ответ: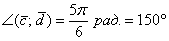 
Скалярное произведение векторов,
заданных координатами в ортонормированном базисе
В данном разделе рассматриваются только ортонормированные базисы плоскости и пространства.
Скалярное произведение векторов 
и 
, заданных в ортонормированном базисе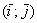 
, выражается формулой 
Скалярное произведение векторов 
, заданных в ортонормированном базисе 
, выражается формулой 
То есть, скалярное произведение равно сумме произведений соответствующих координат векторов.
|
|
Пример
Найти скалярное произведение векторов:
а) 
и 
б) 
и 
, если даны точки 
Решение:
а) Здесь даны векторы плоскости. По формуле 
:
б) Сначала найдём векторы:
По формуле 
вычислим скалярное произведение:
Ответ: 