Решение системы неоднородных линейных
Алгебраических уравнений
В химии и химической технологии имеется большое число математических моделей, использование которых сводится к решению системы неоднородных линейных алгебраических уравнений. В данной лекции мы опишем наиболее известные алгоритмы для решения этой задачи.
Из школьного курса математики известно, как решать систему линейных неоднородных алгебраических уравнений методом последовательного исключения переменных. Поясним суть его на простейшем примере.
Пусть нам необходимо решить систему уравнений
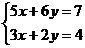
Умножим второе уравнение этой системы на – 5/3 и полученный результат сложим с первым уравнением. После несложных преобразований получим, что + 8y/3 = 1/3 или y = + 1/8. Нахождение х = 5/4 труда не представляет.
Если этот способ решения несколько формализовать, то мы получим схему Гаусса для решения таких уравнений.
Алгоритм метода исключения ведущего элемента по Гауссу
Пусть у нас имеется система линейных неоднородных уравнений, у которой число уравнений равно числу неизвестных.
. (3.1)
Здесь x1, x2, …, xn – неизвестные переменные, Aij – численные коэффициенты, причем хотя бы одна из правых частей этих уравнений не равна нулю.
В матричной форме эту систему можно записать в виде одного уравнения
A∙x = b. (3.2)
Здесь A – квадратная матрица, составленная из коэффициентов при неизвестных, x и b – столбцовые матрицы неизвестных и правых частей уравнений.
На первом шаге алгоритма решения системы 3.1 определяется такое число i, для которого элемент Ai1 не равен нулю.
На втором этапе со всеми уравнениями системы проведем следующие преобразования. Для k ‒ го уравнения с k ≠ i и Ak1 ≠ 0 находим множитель ck по формуле
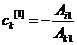. (3.3)
На полученный множитель умножаются все коэффициенты k ‒ го уравнения, а также его правая часть. Если коэффициент Ak1 = 0, то уравнение k оставляют без изменений.
Преобразованные коэффициенты и правые части находятся по формулам
Akj[1] = Aij + Akj∙ck[1] (3.4)
и
bj[1] = bi + bj∙ck[1]. (3.5)
В результате преобразований получаем следующую систему уравнений
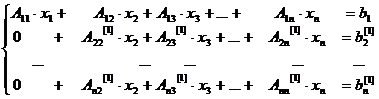. (3.6)
На следующем этапе определяют коэффициент Ai2[1] ≠ 0 и со всеми уравнениями системы проводят преобразования, аналогичные описанным выше. Для k ‒ го уравнения с k ≠ i и Ak2[1] ≠ 0 находим множитель ck по формуле
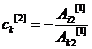. (3.7)
На полученный множитель умножаются все коэффициенты k ‒ го уравнения, а также его правая часть. Если коэффициент Ak2[1] = 0, то уравнение k оставляют без изменений.
Преобразованные коэффициенты и правые части находятся по формулам
Akj[2] = Aij[1] + Akj[1]∙ck[2] (3.8)
и
bj[2] = bi[1] + bj[1]∙ck[2]. (3.9)
В результате преобразований получаем следующую систему уравнений
. (3.10)
Далее исключают коэффициент члены уравнения с x3 и т.д.
В конечном счете, одно из уравнений системы преобразуется к виду
Ann[n-1] ∙ xn = bn[n-1]. (3.11)
Найденное значение xn подставляется в уравнение
An-1,n [n-1] ∙ xn-1 + An-1,n[n-1] ∙ xn = bn-1[n-1]. (3.12)
При известном xn решение этого уравнения дает xn-1. Процедура повторяется до тех пор, пока не будут определены все значения корней исходной системы уравнений и называется «обратным ходом».
В методе Гаусса осуществляется деление на элемент матрицы, который называется ведущим элементом. Программа для решения на компьютере системы линейных неоднородных уравнений методом исключения Гаусса должна всегда проверять равенство или близость к нулю ведущего элемента. Чаще всего в программах для численного решения системы линейных неоднородных уравнений методом Гаусса производят поиск наибольшего по абсолютной величине элемента матрицы коэффициентов и затем используют его в качестве ведущего элемента.
Схема Гаусса позволяет решать системы линейных алгебраических неоднородных уравнений за конечное число арифметических операций. Однако для ее реализации требуется слишком много операций деления. Последнее приводит к тому, что схема Гаусса требует слишком много компьютерного времени, особенно при решении систем уравнений с большим числом неизвестных. Вторым недостатком является то, что во время решения системы уравнений матрица коэффициентов уравнений и ее правых частей должны постоянно находиться в оперативной памяти компьютера, что приводит к неэффективному использованию его ресурсов.
3.2. Итерационное решение систем линейных неоднородных уравнений
Существует большое число итерационных методов решения систем линейных неоднородных уравнений. Среди них отметим методы простой итерации и метод Зайделя.
Преобразуем исходную систему линейных неоднородных уравнений (путем перестановок уравнений и/или умножением всех их членов на постоянные множители) к такому виду, чтобы диагональные коэффициенты Aii были положительными и по возможности большими. Решение начинают с задания произвольных значений xi[0] (i=1, 2, …, n). Затем вычисляют неизвестные на следующей итерации
или по формуле простой итерации
(3.13)
или по формуле Зайделя
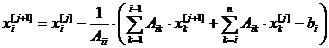(3.14)
при i = 1, 2, …, n; j = 0, 1, 2, …. Здесь j – номер итерации.
Итерации заканчивают тогда, когда становится близкой к нулю или заданной точности определения величина
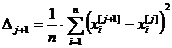. (3.15)
Этот метод решения прост и легко реализуется на компьютере. Однако, следует заметить, что
1) итерационный метод с простой итерацией и метод Зайделя сходятся к решению медленно;
2) иногда они не сходятся к решению вообще (особенно, если неудачно выбрано начальное приближение) или коэффициенты на главной диагонали малы. Одним из возможных критериев применимости итерационных методов является соблюдение равенства
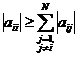. (3.16)
3) важным преимуществом итерационных процессов является то, что они работают иногда и тогда, когда система уравнений включает не только линейные уравнения, но и нелинейные (Нелинейными уравнениями называются уравнения, в которые неизвестные входят в степенях, отличных от единицы).
В итерационном способе решения системы неоднородных линейных уравнений с числом уравнений равным числу неизвестных недостатком является неопределенность в выборе начального приближения. Трудно дать справедливый во всех случаях рецепт, но, в качестве возможного решения этой проблемы существует возможность использования в качестве начального приближения правых частей уравнений, деленных на коэффициенты при соответствующих переменных, т.е.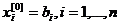 
.
Рассмотрим пример химической задачи, которая приводит к необходимости решать систему линейных алгебраических неоднородных уравнений.
Предположим, что выполняется закон Бугера-Ламберта-Бера для сложной смеси веществ, состоящей из N компонентов. Тогда, если у нас имеются значения оптических плотностей для N длин волн λj, то
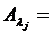
, при j = 1,…, N; i = 1,…,N. (3.17)
Здесь Aλj – оптическая плотность при длине волны λj, εi(λj) – молярный коэффициент экстинкции (поглощении) i – го компонента при длине волны λj, ci – молярная концентрация i – го компонента в исследуемой смеси, l – толщина слоя изучаемой смеси. Решение сформулированной выше системы уравнений относительно N переменных ci при известных величинах εi(λj) приводит к определению количественного состава смеси.
Здесь следует сделать замечание. Поскольку в экспериментально определяемых величинах оптической плотности могут содержаться ошибки эксперимента, а количество M оптических плотностей определяемых при различных длинах – быть значительно больше N, то нетривиальным является вопрос о выборе надлежащего набора длин волн. Одним из методов решения сформулированной проблемы является использование метода наименьших квадратов или корреляционного анализа.
Для применения метода построим невязку Δ.
. (3.18)
Найдем систему уравнений для определения концентраций, приводящих к минимуму величины невязки. Для этого приравняем нулю частные производные по концентрациям от Δ.
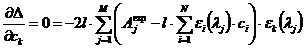. (3.19)
После очевидных преобразований получим систему линейных неоднородных уравнений, которую можно решить одним из изложенных выше методов.
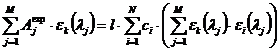, (3.20)
где j=1,…,M; i=1,…,N; k=1,…,N.
Кроме задач, возникающих при спектрофотометрическом анализе состава сложных смесей, аналогичный подход используют при масс-спектрометрическом определении состава компонентов сложной газовой смеси. Действительно, если наблюдаемая величина масс- спектрометрического пика является линейной функцией парциальных давлений газов, т.е.
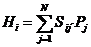, (3.21)
где Hi – наблюдаемая величина масс-спектрометрического пика, N – число компонентов газовой смеси, Sij – чувствительность прибора к j-му газу при определенном значении отношения m/e, измеренная для чистых газов, Pj – парциальное давление j-ого газа в смеси, то математически определение состава смеси ничем не отличается от спектрофотометрического случая.
Часто к системам алгебраических уравнений приводят задачи химической кинетики или изучения равновесных процессов. Действительно, в основе формальной химической кинетики лежит использование закона действующих масс, содержащего значения концентраций компонентов реакционной смеси в степенях соответствующих стехиометрических коэффициентов. Сравнительно легко решаются задачи на определение равновесных концентраций компонентов, например, в водных растворах нескольких солей, при комплексообразовании и т.п.
Схема Гаусса может быть также использована для вычисления значения определителя.
Домашнее задание.
1. Решить методом исключения Гаусса систему уравнений 4-го порядка
2. Разработать алгоритм вычисления определителя n-го порядка методом исключения элементов по Гауссу.
3. Почему метод простой итерации работает, как правило, медленнее, чем метод Зайделя?
4. Системы линейных уравнений, у которых коэффициенты при неизвестных могут различаться на несколько десятичных порядков, решаются, как правило с трудом. Почему? Что нужно сделать, чтобы этого избежать?
5*. Разработать алгоритм для расчета равновесий химических реакций с использованием метода матриц.
6*. Разработать алгоритм для расчета сложных химических кинетических систем с использованием преобразования Лапласа.
(Задачи, помеченные звездочкой предлагается решать после освоения всего курса лекций).