Симплекс – метод решения ЗЛП
Суть симплекс метода основана на том, что решение ЗЛП всегда является либо одна из угловых точек многогранника ОДР, или это бесконечное множество точек одной из границ данного многогранника, поэтому для нахождения решения симплекс- метода находят угловых точек и перебирают в них значения целевой функции.
Простой или примитивный симплекс метод основан на механическом переборе знач. Целевой функции в вершинах ОДР (начиная с начальной точке) так, что значение целевой функции на каждом шаге увелич. (задача на максимум) или уменьш. (в задаче на минимум).
Среди n переменных выбрать, как базисных, можно большим количеством способов, при этом постоянные остается только кол-во базисных переменных.
Из граф. Метода решения задач с n переменными сводится к задаче с двумя переменными можно сделать вывод в каждой угловой точки ОДР, как min две переменные = 0. Аналогично, если в ЗЛП с n переменными k переменные базисные, то как min (число свободных = 0)
В результате решения задачи симплекс методом выяснили, что:
- для обеспечения не отриц. Всех переменных во-первых правы части всех не ограничений b≥0 во-вторых в процессе преобразования нельзя выделить единицу (для получения базисного столбца на месте не отриц. коэффициента). В-третих нельзя отделять единицу.
- значение базисных переменных (когда уже выделены базисные). Столбцы и единицы из нулей находятся в той строке, кот соотв. единица.
Основной алгоритм симплекс метода.
Замечание 1
В дальнейшем для определенности оптимальности решения будем рассматривать ф-ции только на max.
Если же в задаче необходимо исследовать целевую ф-цию 
, то рассматриваем 
, кот достигает max, где F достигает min
1)Для решения задачи симплекс методом необходимо записать ее в каноническом виде 
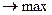
(1) 
Замечание 2
1. Если в каком либо ограниченной системе содержит знак ≤ в водим дополнительные переменные со знаком «+» в левую часть этого органечения при этом доп.переменные так же полагается не отрицается.
2. если какое либо огранчен. Системы больнее или равно то вводит доп.перемен со знаком «-» в левую часть данного огранеч. При этом сама перемен. Не отриц.
3. если одно из огранечений содержит отриц. Число, то умножаем это отрицание на (-1)
Ограничение 1
НОР – базисное удовлетворение решения
2)Запишем ограничение (1) в виде таблицы и перейдем к поиску НОР.
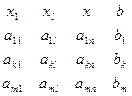
Пусть, необходимо, сделать базисной переменной xl (т.е. выполнить такие преобразования в результате кот. в столбце переменных xl получится 1. остальные 0). Допустим, что мы будем выделять в к-ой строке l-ого столбца.
Тогда элемент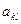 
в дальнейшем будем называть разрешающим элементов соответственно k - столбце разрешающей строке l-строке разрешающим столбце.
Запишем последовательность и результатом элементарных преобразований, затем наложим на преобразование такие условия, кот. позволяют сохранить не отрицательность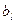 
.
В результате деления 
, i=k
Рассмотрим, что получается в результате в столбце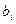 
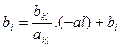
Для сохранения не отрицательности правых частей необходимо 
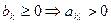
1. Саморазрешающий элемент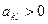 
2. bi≥0 а) если 
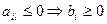
б) если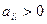 
(
)
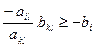Номер строки (разреш.) выбираем так, чтобы отношение коэф. 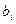и разреш. Строке было min из всех возможных.
Будем в дальнейшем обозначать в качестве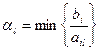 
2 этап. Улучшение НОР.
Пусть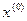 
- НОР предположим, что сущ. Такое решение 
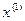,кот будет ближе к оптимальному или само будет оптимальным решением.
Рассмотрим усл., при кот 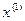будет ближе.
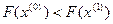рассмотрим разность значений, считая при этом, что при переходе от 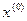к 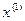была изменена только одна базисная переменная. Будем считать для определенности, что в комплексе базисных переменных, для решения 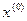содержится 
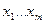, а в решении 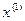одна из этих неизвестных будем заменяться переменной 
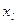(l>m)
Пусть при введении в базисе переменной 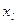выясняется, что из базиса должна выйти переменная k.
Замечание
Для определенности будем считать, что при получении НОР в матрице(табл.) осталось m строк.
= 
Предположим, что решение можно улучшить, введя в базис 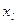, при этом одна из базисных переменных, для определенности 
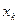будем выведена из базиса.
С Учетом требования сохранения не отрицательности правых частей 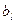, выбираем номер разрешающей строки k таким образом, чтобы отношение 
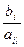было min.
Деле «запускаем» обычные элементарные преобразования для получения базисного столбца для переменной 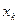(троку делим на 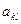и далее преобразование).
Вывод опорное решение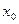 
, будет хуже, чем новое решение 
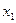только при условии, что найдется хотя бы одна свободная переменная, для кот. оценка 