Тверской государственный технический университет
Кафедра электронных вычислительных машин
Сборник задач
По элементам теории множеств и отношений
Методические указания к практическим занятиям по Дискретной математике
для студентов специальности 22.01
(Вычислительные машины, системы, комплексы и сети)
Тверь 2002
Методические указания содержат задачи по элементам теории множеств и отношений и предназначены для проведения практических занятий и самостоятельной работы студентов по дисциплине «Дискретная математика». Методические указания предназначены для студентов специальности ЭВМ, изучающих курс "Дискретная математика", а также для использования при курсовом проектировании элементов вычислительной техники.
Методические указания рассмотрены на заседании кафедры № от и рекомендованы к изданию в электронном варианте.
Составитель АСЕЕВА Т.В
| ã Тверской государственный технический университет, 2002 |
Элементы теории множеств и отношений. 3
Задание множеств. Операции на множествах. 3
Решение систем уравнений. 5
Декартово произведение множеств. 6
Отношения и функции. 7
Специальные бинарные отношения. 9
Мощность множества. 9
Элементы комбинаторики. 10
Элементы теории множеств и отношений
Задание множеств. Операции на множествах
1. Пусть универсум I = {1,2,3,4,5}, X={1,5}, Y={1,2,4}, Z={2,5}. Найти множества:
1.1. X Ç `Y; [ {5} ];
1.2. (X Ç Z) È `Y; [ {2,3,5} ];
1.3. X È (YÇ Z); [ {1,2,5} ];
1.4. (X È Y) Ç (X È Z); [ {1,2,5}];
1.5. 
(X È Y); [{3}];
1.6. 
`X Ç `Y;
1.7. (X Ç Y);
1.8. (X È Y) È Z;
1.9. X È (Y È Z);
1.10. X \ Z;
1.11. (X \ Z) È (Y \ Z).
Изобразить все получающиеся множества с помощью диаграммы Эйлера-Венна.
2. Даны два произвольных множества А и В такие, что А Ç В = Æ. Определить А \ В и В \ А.
3. Даны два произвольных множества С и D такие, что C Ç `D = Æ. Определить CÈ D и
C È`D. Изобразить подходящие диаграммы Эйлера-Венна.
4. Дано произвольное множество Х. Определить множества
4.1. X Ç`X;
4.2. X È`X;
4.3. X /`X.
5. Какие из следующих утверждений справедливы?
5.1. 0 Î Æ; (нет)
5.2. Æ = {0}; (нет)
5.3. | {Æ}| = 1; (да)
5.4. {{Æ}} = {{{Æ}}}; (нет)
5.5. | {{Æ}}| = 2. (нет, она равна 1).
6. Доказать, что Æ ¹ {Æ}.
7. Доказать, что {{1,2}, {2,3}} ¹ {1,2,3}.
8. Существуют ли такие множества А, В, С, что АÇ В ¹ Æ, А Ç С = Æ, (А Ç В) \ С = Æ?
ª Нет, так как АÇС = Æ Þ $x: x Î AÇB; AÇC=Æ Þ "x: x Î A Þ x Ï C. Следовательно, (АÇВ)\C ¹ Æ. ¨
9. Доказать, что А Í В Û А È В = В Û АÇВ=А Û А\B =Æ Û `A È B = I.
10. Доказать аналитически и графически следующие тождества:
10.1.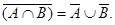 
10.2. 
10.3. 
10.4. 
10.5. 
10.6. 
10.7.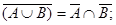 
ª Пусть M, N произвольные множества и M=N. Тогда `MÇ N = Æ, `M È N =I. Пусть далее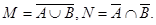 
Тогда, подставляя вместо М и N указанные выражения, получим:
Докажем справедливость этих соотношений, используя аксиомы ассоциативности, дистрибутивности
и дополнения Алгебры Кантора.
¨
10.8.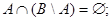 
10.9. 
10.10. 
10.11. 
11. Доказать следующие соотношения:
11.1.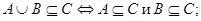 
11.2. 
11.3. 
ª Пусть АÇВÍС и хÎА. Рассмотрим два случая: хÎВ или хÏВ. Если хÎВ, то хÎАÇВÍС, т.е. хÎ `ВÈС. Следовательно, А Í `ВÈС.
Если хÎ`В, то хÎ `ВÈС (по определению объединения множеств).
Пусть АÍ`ВÈС и хÎАÇВ. Тогда хÎА и хÎ В. Значит, хÎС. Следовательно, АÇВÍС. ¨
11.4. 
11.5. 
11.6. 
11.7.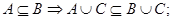 
11.8. 
11.9. 
11.10. 
11.11. 
Примечание. При доказательстве следования (последние задачи) доказательство производится только слева направо.
12. Доказать, что Р(АÇВ)= Р(А)ÇР(В).
ª Р(АÇВ) - булеан множества АÇВ. Поэтому его элементами являются множества, каждое из которых есть подмножество АÇВ. Поэтому решение выглядит следующим образом.
Пусть ХÎР(АÇВ). Тогда ХÍАÇВ. Следовательно, ХÍА и ХÍВ. По определению булеана ХÎР(А) и ХÎР(В). Следовательно, ХÎР(А)ÇР(В), т.е. Р(АÇВ)Í Р(А)ÇР(В).
Пусть ХÎР(А)Ç Р(В). Тогда ХÎР(А) и ХÎР(В). Следовательно, ХÍА и ХÎВ. Следовательно, ХÍАÇВ. Т.е. ХÎР(АÇВ). Следовательно, Р(А)ÇР(В)ÍР(АÇВ).
Из прямого и обратного включений следует равенство. ¨
13. Доказать, что 
.
14. Доказать, что Р(АÈВ)={(Ai ÈBi)|AiÎP(A), BiÎP(B)}.
15. Доказать, что 
16. Какие утверждения верны для всех множеств А, В, С?
16.1. Если АÎВ и ВÎС, то АÎС. (нет)
16.2. Если АÍВ и ВÎС, то АÎС. (нет)
16.3. Если АÇВÍ`С и АÈСÍВ, то АÇС=Æ.
ªАÈСÍВ, следовательно, АÍВ и СÍВ. Следовательно, АÇВ=А. Так как АÇВÍ`С, следовательно, АÍ`С. Следовательно, АÇС=Æ.¨
16.4. Если А¹В и В¹С, то А¹С. (нет)
16.5. Если 
(нет, например, А, В, С попарно не пересекаются).