1. Доказать, что существуют такие множества А, В, и С что
А´ В ¹ В´А.
2. Найти геометрическую интерпретацию следующих множеств:
2.1. [a, b]2;
2.2. [a, b]´[c, d], где [a, b] и [c, d] Í R.
2.3. {0, 1}3.
3. Доказать, что если А, В, С, и D не пусты, то
3.1. А Í В и С Í D Û А ´ С Í В ´ D;
3.2. A=B и C=D Û А´С =В´D/
4. Доказать, что
4.1. (А ÇВ)´(С Ç D)= (А´С) Ç(В´D);
4.2. 
5. Доказать, что (А´В) È (С´D)Í(А ÈС)´(В ÈD). При каких А, В, С, и D получается равенство?
6. Доказать, что
6.1. (А È В)´С=(А´С) È(В´С);
6.2. А´(В ÈС)=(А´В) È(А´С);
6.3. (А ÈВ)´(С ÈD)=(А´С) È (В´С) È(А´D) È(В´D);
6.4. (А\В)´С=(А´С)\(В´С);
6.5. А´(В\С)=(А´В)\(А´С);
6.6. А´В=(А´D) Ç(С´В), где А Í С и В Í D;
6.7. 12-(А´В)=991\А)´1) È(1´(1\В));
6.8.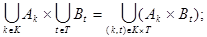 
6.9. 
7. Пусть А,В ¹ Æ и (А´В) È(В´А)=С´D. Доказать, что А=В=С=D.
Отношения и функции
Найти dom r, rang r, r-1, r · r, r · r-1, r-1 · r для отношений:
1.1. r = {(x, y) | x, y ÎN и x делит y};
1.2. r={(x, y)|х,у ÎN и у делит х};
1.3. r={(x, y)|х,у ÎR и х+у £ 0};
1.4. r={(x, y) | х,у ÎR и 2х ³ зу};
1.5. r={(x, y)| х,у Î[-p/2, p/2] и у ³ sin x}.
2. Доказать, что для любых бинарных отношений справедливы утверждения:
2.1. dom r= Æ Û r= Æ Û rang r = Æ;
2.2. dom r-1 = rang r, rang r-1=dom r;
2.3. dom (r1 · r2 )= r1-1(dom r2 Ç rng r1).
ª r1· r2 ={(x,y)| $z: х r1 z, z r2 у}, следовательно, в образовании пар отношения r2 могут участвовать только такие значения z, для которых выполняется включение z Î dom r2 Ç rng r1. Так как область определения композиции отношений r1 · r2 является подмножеством dom r1, то в это подмножество будут включены только те элементы х, для которых определены образы в множестве dom r2 Ç rng r1. Поэтому искомое множество определяется как множество прообразов множества dom r2 Ç rng r1 по отношению r1-1. Таким образом,
dom (r1 · r2 ) = r1-1(dom r2 Ç rng r1). §
2. 4. rng (r1 · r2)= r2(rng r1 Ç dom r 2).
2.5. Пусть r - бинарное отношение на А. Доказать, что r = iA тогда и только тогда, когда r · r1 = r1 · r = r1 для любого отношения r1 не А.
ª Пусть r · r1 = r для всех r1. Тогда $ z: (xz) Î r, (zy) Î r1 и (х,у) Î r1. Это возможно только тогда, когда "х: z=x, т.е. r = iA. Аналогично можно доказать, что r1 · r = r1 тогда и только тогда, когда r = iA. Обратно, если r = iA, то
" r1:r · r1 = r1 · r = r1 в силу определения операции композиции. §
3. Доказать, что для любых бинарных отношений
3.1. (r-1)-1 = r;
ª Пусть (х,у) Î(r-1)-1. Тогда по определению обратного отношения можно записать цепочку включений: (у,х) Î r-1 Þ (х,у) Î r. Таком образом,
(r-1)-1 Í r. Аналогично доказывается обратное включение. Из существования двух включений делается вывод о тождественном равенстве. §
3.2. (r1 È r2)-1 = r1-1 È r2-1;
3.3. (r1 Ç r2)-1 = r1-1 Ç r2-1;
3.4. 
ª Пусть (х,у) Î (r-1), тогда по определению дополнения отношения
3.5. 
(х,у) Ï r-1 и (у,х) Ï r. Следовательно, (у,х) Î `r и (х,у) Î (`r)-1. Следовательно, 
(r-1) Í (`r)-1. Обратное включение доказывается аналогично. §
3.6.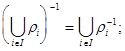 
4. Для каких бинарных отношений справедливо r-1 = `r?
ª Если r Í А´В, А ¹ Æ и В ¹ Æ, то таких отношений не существует. §
5. Пусть А и В - конечные множества, содержащие m и n элементов соответственно.
5.1. Сколько существует бинарных отношений между элементами множеств
А и В?
ª Число бинарных отношений между элементами множеств А и В равно мощности булеана множества А´В. Так как |А´В | = m*n, то искомое число равно 2m*n. §
5.2. Сколько имеется функций из А в В?
ª Если мощность А равна n, то любое функциональное отношение содержит n элементов, каждый из которых начинается с х ÎА, а второй элемент у может быть любым элементом В. Следовательно надо определить число различных способов дописать второй элемент в каждую из пар, т.е. число размещений с повторениями из n элементов по m, равное (nm). §
5.3. Сколько имеется 1-1 функций из А в В?
ª Рассуждая аналогично доказательству задачи 5.2, и учитывая что 1-1 функция есть взаимно однозначное соответствие между А и В, приходим к выводу, что число таких функций равно числу размещений без повторений, Аnm , если n ³m. Если n<m, таких функций не существует. §
5.4. При каких m, n существует взаимно однозначное соответствие между А и В?.
6. Доказать, что для любых бинарных отношений
6.1. r1 · (r2 · r3) = (r1 · r2) · r3; как называется это свойство?
6.2. (r1 · r2)-1 = r2-1 · r1-1;
6.3. 
ª Пусть (х,у) Î 
Тогда $ z: х (È ri)z, zqy. Тогда $i ÎI $z:
x ri z, zqy Þ $i: (x,y) Î (È ri) ·q Þ(х,у) Î 
Обратное включение доказывается аналогично. §
6.4. 
6.5. 
6.6. 
6.7. в пунктах 6.5 и 6.6 включения нельзя заменить равенствами.
ª Пусть r1 ={(11)}, r2={(10)}, q ={(01), (11)}. Тогда пересечение r1 Ç r2= Æ, и композиция
q Ç Æ = Æ Ç q = Æ. Тогда как 
§
7. Доказать, что если r1 Í r2, то
7.1 q ·r1 Í q · r2;
7.2 r1 ·q Í r2 · q;
7.3 r1-1 Í r2-1.
8. Доказать, что если f: A®B и g: B®C, то (f ·g):А®С.
9. Пусть f и g - функции. При каких условиях
9.1. f—1 является функцией?
9.2. f ·g является 1-1 - функцией?
Функция f называется 1-1 - функцией, если "х1х2 (у=f(x1) и y= f(x2)) Þ х1=х2.
1. Пусть f: A®B -взаимно однозначное соответствие. Показать, что
10.1. f -1 · f =iB;
10.2. f ·f -1 = iA.
11. Доказать, что для того, чтобы отношение r Í А´В было взаимно однозначным соответствием между А и В, необходимо и достаточно, чтобы
r · r-1 = iA и r-1 · r = iB.
12. Доказать, что для любой функции f:
12.1. f(А È В) = f(А) È f(В);
12.2. 
12.3. f(А Ç В) Í f(А) Ç f(В);
12.4. 
13. Доказать, что f(А Ç В) Í f(А) Ç f(В) для любых А и В тогда и только тогда, когда f есть
1-1 - функция.
14. Доказать, что f(А)\f(В) Í f(А/В) для любой функции f.