Пример 1.1
Имеются стержни, длиной 5 м. Их необходимо разрезать на заготовки 2-х видов: заготовки А – длиной 1,5 м и заготовки В – длиной 0,8 м для производства 20 изделий. На каждое изделие требуется две длинных заготовки (А) и три коротких (В). Определить число стержней, которое необходимо разрезать каждым из возможных способов, чтобы изготовить нужное число изделий и минимизировать отходы.
Решение
Прежде всего, перебрав все возможные способы, построим карту раскроя одного стержня:
| Способ | Количество заготовок А (по 1,5 м) | Количество заготовок В (по 0,8 м) | Отходы, м |
| I | - | 0,5 | |
| II | 0,4 | ||
| III | 0,3 | ||
| IV | - | 0,2 |
Для изготовления 20 изделий потребуется заготовок А: 20´2 = 40 шт. и заготовок В: 20´3 = 60 шт.
1) Введем переменные. Обозначим за  – количество стержней, которые будут разрезаны I способом,
– количество стержней, которые будут разрезаны I способом, 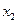 – II способом,
– II способом,  – III способом,
– III способом,  – IV способом.
– IV способом.
2) Целевая функция Z – отходы. Ее будем минимизировать. Найдем отходы, полученные при разрезании стержней:
 – отходы, полученные при разрезании
– отходы, полученные при разрезании  стержней I способом,
стержней I способом,
так как 5 – 3·1,5 = 0,5;
 – отходы, полученные при разрезании
– отходы, полученные при разрезании 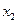 стержней II способом,
стержней II способом,
так как 5 – 2·1,5 – 2·0,8 = 0,4;
 – отходы, полученные при разрезании
– отходы, полученные при разрезании  стержней III способом,
стержней III способом,
так как 5 – 1·1,5 – 4·0,8 = 0,3;
 – отходы, полученные при разрезании
– отходы, полученные при разрезании  стержней IV способом,
стержней IV способом,
так как 5 – 6·0,8 = 0,2.
Тогда  .
.
3) Составим систему ограничений задачи.
а) Ограничение на заготовки А.
При разрезании  стержней I способом получим
стержней I способом получим  заготовок А,
заготовок А,
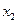 стержней II способом –
стержней II способом –  заготовок А,
заготовок А,  стержней III способом –
стержней III способом –  заготовок А, при разрезании
заготовок А, при разрезании  стержней IV способом заготовок А не образуется. Таким образом, всего получим
стержней IV способом заготовок А не образуется. Таким образом, всего получим 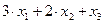 заготовок А, что по условию задачи должно быть не менее 40, то есть
заготовок А, что по условию задачи должно быть не менее 40, то есть  .
.
б) Аналогично получим ограничение на заготовки В:
 .
.
в) Составим ограничения на экономический смысл переменных. Так как количество стержней может быть только неотрицательным числом, то  и
и 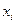 – целые.
– целые.
Итак, математическая модель данной задачи имеет вид:
 ;
;

Пример 1.2
Предприятие за 10 часов должно произвести 31 единицу продукции вида П1 и 36 единиц продукции вида П2. Для производства продукции каждого вида может быть использовано оборудование А1 или А2.
Производительность оборудования этих групп различна и определяется величиной  ед./ч, а стоимость 1 часа работы оборудования составляет
ед./ч, а стоимость 1 часа работы оборудования составляет  усл. ден. ед./ч
усл. ден. ед./ч 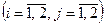 , где i – индекс, отличающий вид оборудования, а j – вид продукции. Требуется определить оптимальный план работы групп оборудования на протяжении 10 часов, при котором будет выполнен план выпуска продукции с минимальной себестоимостью.
, где i – индекс, отличающий вид оборудования, а j – вид продукции. Требуется определить оптимальный план работы групп оборудования на протяжении 10 часов, при котором будет выполнен план выпуска продукции с минимальной себестоимостью.
 5,
5,  3,
3,  4,
4,  6,
6,
 8,
8,  7,
7,  4,
4,  2.
2.
Решение
Для наглядности составим таблицу:
| Продукция П1 | Продукция П2 | Запас времени, ч | |
| Оборудование А1 |  ед./ч ед./ч
 усл. ден. ед./ч усл. ден. ед./ч
|  ед./ч ед./ч
 усл. ден. ед./ч усл. ден. ед./ч
| |
| Оборудование А2 |  ед./ч ед./ч
 усл. ден. ед./ч усл. ден. ед./ч
|  ед./ч ед./ч
 усл. ден. ед./ч усл. ден. ед./ч
| |
| План производства, ед. |
1) Обозначим за  – время работы оборудования А i по выпуску продукции П j,
– время работы оборудования А i по выпуску продукции П j,  .
.
2) Целевая функция будет представлять собой затраты на выпуск продукции, которые необходимо минимизировать. Так как затраты по выпуску продукции П j на оборудование А i составляют  , то целевая функция будет иметь вид:
, то целевая функция будет иметь вид:
 , т. е.
, т. е.  .
.
3) Составим систему ограничений.
а) Ограничение на выпуск продукции П1.
На оборудовании А1 будет произведено  единиц продукции П1.
единиц продукции П1.
На оборудовании А2 будет произведено  единиц продукции П1.
единиц продукции П1.
Таким образом всего продукции П1 будет произведено  , что по условию должно быть равно 31, то есть получим ограничение
, что по условию должно быть равно 31, то есть получим ограничение
 , или
, или  .
.
б) Аналогично получим ограничение по выпуску продукции П2:
 , или
, или 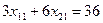 .
.
в) Ограничение на время работы оборудования А1.
Время работы оборудования А1 по выпуску обоих видов продукции не превышает плановый период 10 ч, следовательно, ограничение будет иметь вид:  .
.
г)Аналогично получим ограничение на время работы оборудования А2:  .
.
д) Введем ограничения на экономический смысл переменных, так как время не может быть отрицательным, то  .
.
Таким образом, математическая модель данной задачи будет иметь вид:
 ;
;

Пример 1.3
Предприятие может выпускать продукцию двух видов: П1 и П2. При этом используется три вида ресурсов: время работы оборудования, сырье и электроэнергия. Нормы расхода, запасы ресурсов и прибыль от реализации единицы продукции представлены в таблице:
| Ресурсы | Нормы расхода на единицу продукции | Запас ресурса | |
| П1 | П2 | ||
| Время работы оборудования, ч Сырье, кг Электроэнергия, кВтч. | |||
| Прибыль от единицы продукции, руб. |
Найти оптимальный план выпуска продукции.
Решение
Введем переменные:
 ,
, 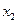 – объем выпускаемой продукции П1 и П2 соответственно, единиц.
– объем выпускаемой продукции П1 и П2 соответственно, единиц.
Z – прибыль от реализации всей выпущенной продукции.
Математическая модель данной задачи будет иметь вид:
 ;
;

Методы решения задач линейного программирования будут рассмотрены ниже.
Задачи
1.1.1
Необходимо за 24 часа изготовить максимальное количество изделий, общая себестоимость которых не должна превышать 2000 руб., используя при этом два станка. Производительность первого станка составляет 5 изделий в час, второго – 6 изделий в час. Себестоимость одного изделия, изготовленного на первом станке, составляет 9 руб., на втором станке – 10 руб. Составить математическую модель выпуска продукции на указанных станках.
1.1.2
Цех может выпускать 2 вида продукции, производство которых характеризуется следующими данными:
| Продукция | Время на производство изделия, ч | Количество металла на изделие, кг | Прибыль от реализации изделия, руб. |
| I вид II вид |
В планируемом месяце имеется 100 часов рабочего времени и 60 кг металла. Продукции I вида должно бать выпущено не менее 25 изделий. Составить математическую модель задачи выпуска продукции с максимальной прибылью от реализации.
1.1.3
Завод должен переслать 1000 деталей в ящиках двух типов. Ящик I типа вмещает 70 деталей, ящик II типа – 40 деталей. Стоимость пересылки одного ящика I типа составляет 30 руб., II типа – 20 руб. Для пересылки можно использовать не более 12 ящиков I типа. Составить математическую модель задачи пересылки всех деталей с наименьшими затратами
1.1.4
Имеются путевки в дома отдыха 3-х видов: на 7, 12 и 20 дней. Стоимость их 100 руб., 150 руб. и 250 руб. соответственно. Организация планирует закупить 21 путевку и потратить не более 3000 руб. Составить математическую модель задачи определения нужного числа путевок каждого вида, чтобы общее число дней отдыха по всем путевкам оказалось наибольшим.
1.1.5
Для рекламирования своей продукции фирма может использовать радио, телевиденье и общественный транспорт. Стоимость одной минуты рекламы на радио составляет 3 усл. ден. ед., а на телевиденье – 50 усл. ден. ед., в общественном транспорте – 2 усл. ден. ед. Объемы продаж увеличиваются от рекламы на радио, телевиденье и в общественном транспорте в соотношении 2:30:1. Фирма может использовать в месяц не более 10 минут эфирного времени на телевиденье и не более 100 минут на радио. На всю рекламу фирма запланировала потратить в месяц не более 900 усл. ден. ед. Составить математическую модель задачи эффективного вложения в рекламу денежных средств.
1.1.6
Нужно перевести по железной дороге 20 больших и 150 малых контейнеров, используя при этом минимальное количество вагонов. Вес малого контейнера составляет 2 тонны, а большого – 5 тонн. Грузоподъемность вагона – 60 тонн, недогрузка вагонов не допускается. Составить математическую модель задачи перевозки всех контейнеров.
1.1.7
Из пункта S в пункт T необходимо перевести 250 ед. оборудования типа I, 120 – типа II, 340 – типа III на автомобилях вида А, В, С и D. Количество оборудования одновременно вмещаемого на определенный автомобиль и затраты на одну поездку каждого автомобиля приведены в таблице:
| Тип оборудования | Количество оборудования вмещаемого на автомобиль | |||
| А | В | С | D | |
| I II III | ||||
| Затраты, руб. |
Составить математическую модель задачи перевозки оборудования с минимальными затратами.
1.1.8
Цех может выпускать 3 вида продукции, производство которых характеризуется следующими данными:
| Продукция | Время на производство ед. продукции, ч | Количество металла на ед. продукции, кг | Прибыль от реализации ед. продукции, руб. |
| I вид II вид III вид |
В планируемом месяце имеется 500 часов рабочего времени и 700 кг металла. Составить математическую модель задачи выпуска продукции с максимальной прибылью от реализации.
1.1.9
Предприятие за 8 часов должно выпустить 25 единиц продукции вида П1 и 35 единиц продукции вида П2. Для производства продукции каждого вида может быть использовано оборудование А1 или А2.
Производительность оборудования А1 по выпуску продукции П1 составляет 4 ед./ч, а по выпуску продукции П2 – 5 ед./ч., стоимость 1 часа работы оборудования А1 составляет 15 руб. Производительность оборудования А2 по выпуску продукции П1 составляет 3 ед./ч, а по выпуску продукции П2 – 2 ед./ч., стоимость 1 часа работы оборудования А2 составляет 7 руб. Составить математическую модель задачи выпуска запланированной продукции с минимальной себестоимостью.
1.1.10
В плановом году строительные организации города переходят к сооружению домов типов Д1, Д2, Д3 и Д4. Данные о количестве квартир разного типа в каждом из указанных типов домов, их плановая себестоимость приведены в таблице:
| Тип квартиры | Тип дома | |||
| Д1 | Д2 | Д3 | Д4 | |
| Однокомнатная Двухкомнатная Трехкомнатная Четырехкомнатная | – | – | ||
| Плановая себестоимость, ден. ед. |
Годовой план ввода жилой площади составляет соответственно 1000, 1300, 1500 и 300 квартир указанных типов. Составить математическую модель задачи выполнения плана ввода квартир (а возможно, и его перевыполнения) с минимальной себестоимостью.
1.1.11
Необходимо за 8 часов изготовить 200 изделий, используя при этом три станка. Производительность первого станка составляет 10 изделий в час, второго – 12 изделий в час, третьего – 9 изделий в час. Себестоимость одного изделия, изготовленного на первом станке, составляет 3 руб., на втором станке – 2,8 руб., на третьем станке – 2,5 руб. Составить математическую модель задачи выпуска продукции на указанных станках с минимальной себестоимостью.
1.1.12
На производство поступило 100 стержней длиной 1м, которые необходимо разрезать на заготовки А длиной 0,3м и заготовки В длиной 0,2м. Для изготовления одного изделия требуется 1 заготовка А и 3 заготовки В. Составить математическую модель задачи раскроя стержней для изготовления максимального количества изделий.
1.2. Формы записи задач линейного программирования
Общая задача линейного программирования (ОЗЛП) – это ЗЛП, у которой все переменные неотрицательны, т.е. ее математическая модель имеет вид:


где  – заданные действительные числа.
– заданные действительные числа.
Симметричной (стандартной) формой записи ЗЛП называется задача максимизации целевой функции (1.3) при ограничениях вида (1.4) и (1.7) или задача минимизации целевой функции (1.3) при ограничениях вида (1.6) и (1.7), т. е.
 или
или
где  – заданные действительные числа.
– заданные действительные числа.
Канонической формой записи ЗЛП называется задача минимизации или максимизации целевой функции (1.3) при ограничениях вида (1.5) и (1.7), т. е.

Рассмотрим приемы, позволяющие переходить от одной формы записи задачи к другой
1) Переход от задачи на минимум целевой функции к задаче на максимум целевой функции осуществляется умножением ее на (–1). Действительно, если функция  достигает минимума при значениях
достигает минимума при значениях 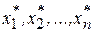 , то функция (
, то функция ( ) достигает при тех же значениях переменных максимума.
) достигает при тех же значениях переменных максимума.
2) Переход от неравенства вида «£ » к неравенству вида «³ » (и наоборот) также осуществляется умножением исходного неравенства на (–1).
3) Переход от неравенства к равенству осуществляется введением дополнительной неотрицательной переменной. Так если в исходной модели  , то, вводя
, то, вводя  , получим
, получим  , а если в исходной модели
, а если в исходной модели  , то, вводя
, то, вводя 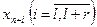 , получим
, получим  , где
, где  .
.
4) При переходе от равенств к неравенствам можно руководствоваться следующим: любое уравнение  эквивалентно системе двух неравенств:
эквивалентно системе двух неравенств: 
5) Введение условия неотрицательности переменной. Пусть на переменную  это условие не было наложено (т.е.
это условие не было наложено (т.е.  может быть любого знака). Тогда вместо этой переменной можно ввести две неотрицательные переменные
может быть любого знака). Тогда вместо этой переменной можно ввести две неотрицательные переменные  и
и  , и представить
, и представить  , где
, где 
 . Это всегда возможно.
. Это всегда возможно.
Изложенными приемами любая ЗЛП может быть сведена к ОЗЛП, симметричной и канонической формам записи ЗЛП, которые используются для решения ЗЛП. Однако, поскольку в процессе таких преобразований мы вводили дополнительные переменные, то после того, как задача решена, нужно произвести обратный переход к исходным переменным, определяющим непосредственный экономический смысл задачи.
Пример 1.4
Пусть математическая модель задачи имеетследующий вид:
 ;
;

Записать для данной модели
а) ОЗЛП,
б) симметричную форму,
в) каноническую форму.
Решение
а) Чтобы получить общую задачу линейного программирования, необходимо, чтобы на все переменные было наложено условие неотрицательности. Для наложения этого ограничения на переменную  воспользуемся правилом 5. Введем две новые неотрицательные переменные
воспользуемся правилом 5. Введем две новые неотрицательные переменные  и
и  и представим
и представим  , где
, где  и
и  .
.
Тогда ОЗЛП будет иметь вид:
 ;
;

или (раскрыв скобки):
 ;
;

Обратите внимание, что в ОЗЛП число переменных на одну увеличилось.
б) Для составления симметричной формы воспользуемся полученной ОЗЛП (т.к. в симметричной форме также на все переменные должно быть наложено условие неотрицательности). Чтобы получить все ограничения вида «³ » (т.к. целевая функция на минимум) необходимо ограничение (1.9) умножить на (–1) (правило 2), а ограничение-равенство (1.10) заменить предварительно двумя ограничениями-неравенствами (правило 4):

откуда, умножив второе ограничение системы на (–1), получим ограничение (1.11) вида «³ ». Таким образом, симметричная форма будет иметь вид:
 ;
;

где  .
.
Обратите внимание, что в симметричной форме увеличилось число ограничений (за счет замены одного ограничения-равенства двумя ограничениями-неравенствами) и число переменных (за счет замены одной переменной любого знака на разность двух неотрицательных переменных).
в) Для составления канонической формы воспользуемся полученной ОЗЛП (т.к. в канонической форме также на все переменные должно быть наложено условие неотрицательности). Чтобы получить все ограничения вида «= » необходимо из ограничений-неравенств (1.8 – 1.9) получить эквивалентные ограничения-равенства. Согласно правилу 3 для этого от левой части ограничения (1.8) отнимем новую неотрицательную переменную  , а к левой части ограничения (1.9) прибавим новую неотрицательную переменную
, а к левой части ограничения (1.9) прибавим новую неотрицательную переменную  . Таким образом, каноническая форма будет иметь вид:
. Таким образом, каноническая форма будет иметь вид:
 ;
;

где  .
.
Пример 1.5
Пусть математическая модель задачи имеетследующий вид:
 ;
;

Записать для данной модели
а) ОЗЛП,
б) симметричную форму,
в) каноническую форму.
Решение
а) Чтобы все переменные задачи были неотрицательны, представим  , где
, где  и
и  .
.
Тогда ОЗЛП будет иметь вид:
 ;
;

где  .
.
б) Для составления симметричной формы воспользуемся полученной ОЗЛП. Симметричная форма будет иметь вид:
 ;
;

где  .
.
в) Для составления канонической формы воспользуемся полученной ОЗЛП. Каноническая форма будет иметь вид:
 ;
;

где  .
.
Задачи
Записать для данной модели (1.2.1 – 1.2.6)
а) ОЗЛП,
б) симметричную форму,
в) каноническую форму.
1.2.1
 ; ;
 1.2.3
1.2.3
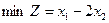 ; ;
 1.2.5
1.2.5
 ; ;

| 1.2.2
 ; ;
 1.2.4
1.2.4
 ; ;
 1.2.6
1.2.6
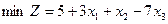 ; ;

|
1.3. Геометрическая интерпретация и графический метод решения задач линейного программирования с двумя переменными
Графическим методом можно решать любые задачи линейного программирования с двумя переменными.
Пусть дана задача


где  – заданные действительные числа.
– заданные действительные числа.
Дадим геометрическую интерпретацию элементов этой задачи.
Каждое из ограничений-неравенств (1.13,1.15,1.16) системы задает на плоскости  некоторую полуплоскость. Каждое из ограничений-равенств (1.14) системы задает на плоскости
некоторую полуплоскость. Каждое из ограничений-равенств (1.14) системы задает на плоскости  некоторую прямую. И полуплоскость и прямая – выпуклые множества. Т.к. пересечение любого числа выпуклых множеств является выпуклым множеством, то область допустимых решений (ОДР) задачи является выпуклым множеством.
некоторую прямую. И полуплоскость и прямая – выпуклые множества. Т.к. пересечение любого числа выпуклых множеств является выпуклым множеством, то область допустимых решений (ОДР) задачи является выпуклым множеством.
Целевая функция – это семейство параллельных прямых, называемых линиями уровня целевой функции. Вектор-градиент целевой функции  показывает направление ее наискорейшего возрастания и перпендикулярен линиям уровня целевой функции.
показывает направление ее наискорейшего возрастания и перпендикулярен линиям уровня целевой функции.
Опорной прямой называется линия уровня, которая имеет хотя бы одну общую точку с областью допустимых решений и по отношению к которой эта область находится в одной из полуплоскостей.
Область допустимых решений любой задачи имеет не более двух опорных прямых, на одной из которых может находиться оптимальное решение (рис. 1.1 – 1.2).

Рис. 1.1