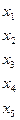1) Если прямая задача на максимум, то двойственная к ней – на минимум, и наоборот.
2) Если прямая (двойственная) задача на максимум, то ограничения-неравенства системы представляются в виде неравенств типа 
, если на минимум, то ограничения-неравенства системы представляются в виде неравенств типа 
.
3) Каждому ограничению прямой задачи соответствует переменная двойственной задачи, и наоборот, каждому ограничению двойственной задачи соответствует переменная прямой задачи, следовательно, число ограничений прямой задачи равно числу переменных двойственной, а число ограничений двойственной – числу переменных прямой.
4) Матрица системы ограничений двойственной задачи получается из матрицы системы ограничений исходной задачи транспонированием.
5) Свободные члены системы ограничений прямой задачи являются коэффициентами при соответствующих переменных целевой функции двойственной задачи, и наоборот, коэффициенты целевой функции прямой задачи являются свободными членами соответствующих ограничений двойственной задачи.
6) Если на переменную прямой задачи наложено условие неотрицательности, то соответствующее ограничение двойственной задачи записывается как ограничение-неравенство, если же нет, то как ограничение-равенство.
7) Если какое-либо ограничение прямой задачи записано как равенство, то на соответствующую переменную двойственной задачи условие неотрицательности не налагается.
Пример 1.24
Составить задачу, двойственную к ЗЛП:
;
Решение
Воспользовавшись правилами построения двойственной задачи, получим следующую пару двойственных ЗЛП:
прямая задача
;
| двойственная задача
 ;
|
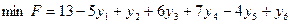Пример 1.25
Составить задачу, двойственную к ЗЛП, рассмотренной в примере 1.8 (на максимум). Из решения прямой задачи (пример 1.8) найти решение двойственной задачи.
Решение
Исходная ЗЛП:
Построим пару двойственных ЗЛП:
прямая задача
| двойственная задача
 ;
|
В примере 1.6 было получено решение прямой задачи графическим методом. Это 
, 
.
Для нахождения решения двойственной задачи запишем обе задачи в канонической форме, без учета неотрицательности исходных переменных и добавляя во все ограничения неотрицательные переменные. Если переменная добавляется в ограничение-равенство, то она равна нулю:
прямая задача
| двойственная задача
;
|
Между переменными двойственных задач существует следующее соответствие:
Определим из канонической формы прямой задачи, какие переменные равны нулю в оптимальном плане и из приведенного соответствия определим отличные от нуля двойственные переменные. Так
,
,
,
,
.
Для нахождения отличных от нуля двойственных переменных 
и 
решим систему уравнений, полученную из системы ограничений канонической формы двойственной задачи:
Откуда 
. Таким образом, 
, или для двойственной задачи в симметричной форме 
. Причем 
.
Пример 1.26
Составить задачу, двойственную к ЗЛП, примера 1.22. Из решения прямой задачи симплексным методом (пример 1.22) найти решение двойственной задачи.
Решение
Исходная ЗЛП:
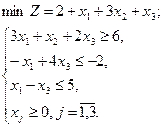
Построим пару двойственных ЗЛП:
прямая задача
| двойственная задача
 ;
|
Для нахождения решения двойственной задачи запишем обе задачи в канонической форме:
прямая задача
| двойственная задача
;
|
Между переменными двойственных задач существует следующее соответствие:
Для нахождения оптимального плана двойственной задачи воспользуемся симплексной таблицей, в которой найден оптимальный план прямой задачи (табл. 1.18). Двойственные переменные, соответствующие базисным переменным прямой задачи будут равны нулю, а соответствующие свободным переменным – будут равны абсолютной величине оценок этих столбцов. Так 
, 
, 
– базисные переменные, следовательно, соответствующие им двойственные переменные 
, 
, будут равны нулю, т.е. 
, 
, 
. Найдем значения двойственных переменных, соответствующих свободным переменным прямой задачи:
,
,
.
Таким образом, 
, или для двойственной задачи в симметричной форме 
. Причем 
.
Задачи
Составить двойственные ЗЛП. Решая графическим методом двойственную задачу, получить решение прямой задачи (1.6.1 – 1.6.4).
1.6.1
 ;
1.6.3
 ;
| 1.6.2
 ;
1.6.4
 ;
|
1.6.5 – 1.6.10
Составить двойственные ЗЛП к задачам 1.2.1 – 1.2.6 (соответственно).
1.6.11 – 1.6.28
Составить двойственные ЗЛП к задачам 1.3.3 – 1.3.12, 1.4.1 – 1.4.8 (соответственно). Решая графическим методом прямую задачу, получить решение двойственной задачи.
1.6.29 – 1.6.38
Составить двойственные ЗЛП к задачам 1.5.1 – 1.5.8 (соответственно). Решая симплексным методом прямую задачу, получить решение двойственной задачи.
1.6.39 – 1.6.41
Составить двойственные ЗЛП к задачам 1.3.7, 1.3.8, и 1.3.11 (соответственно). Решая графическим методом двойственную задачу, получить решение прямой задачи.
Глава 2. Транспортная задача линейного программирования (ТЗ)
2.1. Математическая модель транспортной задачи
У m поставщиков 
сосредоточен однородный груз в объемах 
единиц, соответственно. Данный груз необходимо доставить потребителям 
, спрос которых выражается величинами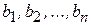 
единиц, соответственно. Известна стоимость 
перевозки единицы груза (тариф) из 
-го (
) поставщика 
-му (
) потребителю.
Требуется составить план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и суммарные затраты на перевозку всего груза минимальны.
Для наглядности, условие транспортной задачи можно представить таблицей, которую будем называть распределительной. Распределительную таблицу называют иногда табличной или матричной моделью ТЗ (см. табл. 2.1).
Таблица 2.1
| Потребители | Запас  , единиц
| ||||||||
| Поставщики | 
| 
| ... | 
| |||||
| 
| 
| 
| 
| |||||
| ... | |||||||||
| 
| 
| 
| 
| |||||
| ... | |||||||||
| ... | ... | ||||||||
| ... | ... | ... | ... | ||||||
| 
| 
| 
| 
| |||||
| ... | |||||||||
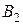
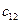
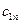
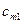
Потребность  , единиц
| 
| 
| ... | 
|
Составим математическую модель ТЗ.
Введем переменные 
– объемы перевозок от -го поставщика 
-му потребителю.
Матрицу 
будем называть матрицей перевозок.
Цель ТЗ – минимизировать суммарные затраты на перевозку всего груза, следовательно, целевая функция будет иметь вид:
(2.1)
Составим систему ограничений (2.1) в случае, когда 
, которая будет определять ОДР данной задачи.
Первые m уравнений системы (2.2) – это ограничения на запас груза у поставщиков, следующие n уравнений системы (2.2) – это ограничения на запросы потребителей в грузе, неравенства системы – это ограничения на экономический смысл переменных (объем груза не может быть отрицательным).
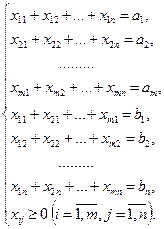(2.2)
Будем называть план перевозок
допустимым, если он удовлетворяет системе ограничений (2.2).
Допустимый план перевозок, доставляющий минимум целевой функции, называется оптимальным.