Расчет переходных процессов
в линейных электрических цепях
Методические указания к выполнению домашнего задания
Москва
Издательство МГТУ им. Н. Э. Баумана
УДК 621.3
ББК 31.2
М48
Методические указания к выполнению домашнего задания «Расчет переходных процессов в линейных электрических цепях» по курсу «Основы электротехники» издаются в соответствии с учебным планом специальностей: 211000 «Конструирование и технология электронных средств», 220400 «Управление в технических системах», 152200 «Наноинженерия», 221000 «Мехатроника и робототехника».
Методические указания рассмотрены и одобрены:
кафедрой ЭИУ7-КФ «Электротехника», протокол № 1 от 17.02. 2012 г.
Зав. кафедрой ЭИУ7-КФ __________ Д. В. Мельников
Методической комиссией факультета ЭИУК,
протокол № ___ от _______ 2012 г.
Председатель методической комиссии факультета ЭИУК
__________ М. Ю. Адкин
Методической комиссией Калужского филиала МГТУ
им. Н. Э. Баумана, протокол № ___ от _______ 2012 г.
Председатель методической комиссии Калужского филиала МГТУ
им. Н. Э. Баумана __________ О. Л. Перерва
Авторы:
канд. техн. наук, доцент кафедры ЭИУ7-КФ ________ Д. В. Мельников;
канд. физ.-мат. наук, доцент кафедры ЭИУ7-КФ ________ М. Р. Фишер.
Рецензент: д-р техн. наук, профессор кафедры ЭИУ3-КФ
____________ Ю. П. Корнюшин
Методические указания содержат необходимые теоретические сведения, варианты задания и контрольные вопросы для выполнения домашней работы «Расчет переходных процессов в линейных электрических цепях» по курсу «Основы электротехники».
Методические указания предназначены для студентов направлений: 211000 «Конструирование и технология электронных средств», 220400 «Управление в технических системах», 152200 «Наноинженерия», 221000 «Мехатроника и робототехника».
© Мельников Д. В., Фишер М. Р., 2012
1. Возникновение переходных процессов и законы коммутации
В электрических цепях могут происходить включения и отключения пассивных или активных цепей, короткие замыкания отдельных участков, различного рода переключения, внезапные изменения параметров и т.д. В результате таких изменений, называемых коммутационными или просто коммутациями, которые будем считать происходящими мгновенно, в цепи возникают переходные процессы, заканчивающиеся спустя некоторое (теоретически бесконечно большое) время после коммутации.
Примем следующие обозначения:
 – начало отсчета времени переходного процесса;
– начало отсчета времени переходного процесса;
 – момент времени непосредственно перед мгновенной коммутацией;
– момент времени непосредственно перед мгновенной коммутацией;
 – момент времени непосредственно сразу после мгновенной коммутации.
– момент времени непосредственно сразу после мгновенной коммутации.
В индуктивном элементе ток (и магнитный поток) непосредственно после коммутации в момент, который и назван моментом коммутации, сохраняет значение, которое он имел непосредственно перед коммутацией, т.е. при  и дальше начинает изменяться именно с этого значения. Записанное в математической форме это явление называется первым законом коммутации:
и дальше начинает изменяться именно с этого значения. Записанное в математической форме это явление называется первым законом коммутации:
 .
.
Так, при включении ветви с катушкой, в которой не было тока, ток в этой ветви в момент коммутации равен нулю. Если для такой ветви допустить, что в момент коммутации ток изменяется скачком, то напряжение на индуктивном элементе  будет бесконечно большим и не будет выполняться II закон Кирхгофа.
будет бесконечно большим и не будет выполняться II закон Кирхгофа.
На емкостном элементе напряжение (и заряд) сохраняет в момент коммутации то значение, которое оно имело непосредственно перед коммутацией, и в дальнейшем изменяется, начиная именно с этого значения. Это явление называется вторым законом коммутации:
 .
.
Так, при включении ветви с конденсатором, который не был заряжен, напряжение в момент коммутации равно нулю. Если допустить, что в момент коммутации напряжение на емкостном элементе изменится скачком, то ток  будет бесконечно большим, и в цепи не будет выполняться II закон Кирхгофа.
будет бесконечно большим, и в цепи не будет выполняться II закон Кирхгофа.
С энергетической точки зрения невозможность мгновенного изменения тока  и напряжения
и напряжения  объясняется невозможностью скачкообразного изменения запасенной в индуктивном и емкостном элементах энергии, так как такое изменение энергии требует бесконечно большой мощности.
объясняется невозможностью скачкообразного изменения запасенной в индуктивном и емкостном элементах энергии, так как такое изменение энергии требует бесконечно большой мощности.
Цель анализа переходных процессов в электрических цепях – определение временных законов изменения токов или напряжений на заданных участках цепи в переходном режиме.
Рассмотрим общие вопросы расчета переходных процессов на простом примере – включение  – цепи к источнику ЭДС
– цепи к источнику ЭДС  , которая изменяется во времени непрерывно и задана каким-либо аналитическим выражением:
, которая изменяется во времени непрерывно и задана каким-либо аналитическим выражением:
 , (1)
, (1)
где  – ток переходного процесса, который будем называть переходным током;
– ток переходного процесса, который будем называть переходным током;  – напряжение на конденсаторе.
– напряжение на конденсаторе.
Когда с переходным процессом можно не считаться, наступает принужденный режим. Принужденный режим, создаваемый источником произвольной периодически изменяющейся ЭДС (или током) называется установившимся.
В установившемся режиме
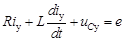 , (2)
, (2)
где  ,
,  , – ток и напряжение установившегося режима (установившийся ток и установившееся напряжение).
, – ток и напряжение установившегося режима (установившийся ток и установившееся напряжение).
Если вычесть из уравнения (1) уравнение (2) и обозначить  , то
, то
 . (3)
. (3)
Разности токов и напряжений переходного процесса и принужденного (установившегося) режима называются током и напряжением свободного процесса или просто свободным током и напряжением.
Процесс, происходящий в цепи, можно рассматривать состоящим из двух накладывающихся друг на друга процессов – установившегося, который как бы наступил сразу, и свободного, имеющего место только во время переходного процесса:
 ;
;  ;
;
 ;
;  .
.
Конечно, физически существуют только переходные токи и напряжения, и разложение их на составляющие является удобным математическим приемом, облегчающим расчет переходных процессов.
Разложение переходных токов и напряжений соответствует правилу решения линейных неоднородных дифференциальных уравнений, согласно которому общее решение равно сумме частного решения неоднородного уравнения и общего решения однородного уравнения.
Свободный ток представляет собой общее решение однородного дифференциального уравнения (3), и в его выражении должны быть постоянные интегрирования, число которых равно порядку дифференциального уравнения.
Установившийся ток – частное решение неоднородного дифференциального уравнения (1), которое получается из общего решения неоднородного дифференциального уравнения при равных нулю постоянных интегрирования.
При интегрировании дифференциальных уравнений появляются постоянные интегрирования, которые определяют из начальных условий.
Начальные условия – значения переходных токов в индуктивных элементах и напряжений на емкостных элементах при  , т.е. те значения, которые в момент коммутации не изменяются скачком. Это так называемые независимые начальные условия.
, т.е. те значения, которые в момент коммутации не изменяются скачком. Это так называемые независимые начальные условия.
Начальные значения всех остальных токов и напряжений называются зависимыми начальными условиями. Их определяют по независимым начальным условиям при помощи уравнений, составленных по I и II законам Кирхгофа. Это является основной трудностью решения классическим методом.
2. Классический метод расчета переходных процессов
2.1. Теоретические сведения.
В основе классического метода расчета переходных процессов в электрических цепях лежит составление интегрально-дифференциальных уравнений для мгновенных значений токов и напряжений. Эти уравнения составляют для схем, полученных после коммутации, основываясь на известных методах расчета электрических цепей, таких как метод непосредственного применения законов Кирхгофа, метод контурных токов, метод узловых потенциалов. Решение полученной системы уравнений относительно выбранной переменной и составляет сущность классического метода.
При этом связь между токами и напряжениями на участках цепи (на активных сопротивлениях и на реактивных элементах) определяется следующим образом (рис. 1.):
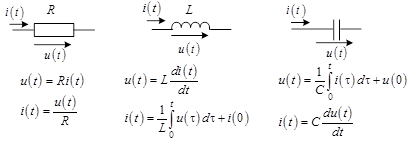
Рис. 1. Связь между токами и напряжениями на участках цепи
Учитывая, что решение дифференциальных уравнений проще интегрально-дифференциальных, полученную систему сводят к дифференциальным уравнениям.
Порядок дифференциального уравнения равен числу независимых накопителей энергии в цепи, под которыми понимаются катушки индуктивности и конденсаторы в упрощенной схеме, получаемой из исходной путем объединения индуктивностей и соответственно емкостей элементов, соединения между которыми являются последовательными или параллельными.
В общем случае порядок дифференциального уравнения определяется соотношением:
 .
.
где  и
и  – число катушек индуктивности и конденсаторов соответственно после указанного упрощения исходной схемы;
– число катушек индуктивности и конденсаторов соответственно после указанного упрощения исходной схемы;  – число узлов, в которых сходятся только ветви, содержащие катушки индуктивности (в соответствии с первым законом Кирхгофа ток через любую катушку индуктивности в этом случае определяется токами через остальные катушки);
– число узлов, в которых сходятся только ветви, содержащие катушки индуктивности (в соответствии с первым законом Кирхгофа ток через любую катушку индуктивности в этом случае определяется токами через остальные катушки);  – число контуров схемы, ветви которых содержат только конденсаторы (в соответствии со вторым законом Кирхгофа напряжение на любом из конденсаторов в этом случае определяется напряжениями на других).
– число контуров схемы, ветви которых содержат только конденсаторы (в соответствии со вторым законом Кирхгофа напряжение на любом из конденсаторов в этом случае определяется напряжениями на других).
Обозначим искомую функцию времени (напряжение, ток, потокосцепление и т. п.) через  , тогда дифференциальное уравнение
, тогда дифференциальное уравнение  порядка, описывающее переходный процесс в электрической цепи, находящейся под воздействием источника
порядка, описывающее переходный процесс в электрической цепи, находящейся под воздействием источника  , имеет вид:
, имеет вид:
 , (4)
, (4)
где  – коэффициенты, зависящие от параметров цепи (в дальнейшем рассматриваются цепи только с постоянными параметрами);
– коэффициенты, зависящие от параметров цепи (в дальнейшем рассматриваются цепи только с постоянными параметрами);  – функция, описывающая характер воздействия на цепь.
– функция, описывающая характер воздействия на цепь.
Дифференциальное уравнение (4) относится к линейным неоднородным уравнениям  -го порядка. Как известно из курса высшей математики, его решение есть сумма общего решения
-го порядка. Как известно из курса высшей математики, его решение есть сумма общего решения  однородного дифференциального уравнения
однородного дифференциального уравнения  - го порядка:
- го порядка:
 ,
,
и частного решения  уравнения (4)
уравнения (4)
 .
.
Частное решение данного неоднородного уравнения, получаемое с учетом внешнего воздействия 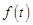 , называется принужденной (установившейся) составляющей решения
, называется принужденной (установившейся) составляющей решения  и определяется из соотношений для установившегося режима данной цепи после коммутации.
и определяется из соотношений для установившегося режима данной цепи после коммутации.
Общее решение однородного уравнения определяет процессы, которые протекают в цепи без участия внешнего воздействия, и называется свободной составляющей  . Вид свободной составляющей переходного процесса определяется числом и значениями корней характеристического уравнения:
. Вид свободной составляющей переходного процесса определяется числом и значениями корней характеристического уравнения:
 ,
,
В случае, когда корни  характеристического уравнения вещественные и различные, решение имеет вид:
характеристического уравнения вещественные и различные, решение имеет вид:
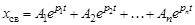
где 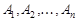 , – постоянные интегрирования, которые находятся из начальных условий задачи.
, – постоянные интегрирования, которые находятся из начальных условий задачи.
В случае, когда корни уравнения – вещественные и равные, т. е  , свободная составляющая определяется уравнением:
, свободная составляющая определяется уравнением:
 .
.
Если корни комплексно-сопряженные  , тогда
, тогда
 ,
,
где  ,
,  – постоянные интегрирования, определяемые также из начальных условий задачи.
– постоянные интегрирования, определяемые также из начальных условий задачи.
В таблице 1 обобщены данные для определения свободных составляющих дифференциального уравнения  -го порядка.
-го порядка.
Таблица 1.
|
| ||
Корни 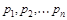 вещественные и различные вещественные и различные
| 
| ||
Корни 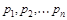 вещественные и вещественные и 
| 
| ||
| 
|
Начальные условия задачи определяют значения токов в индуктивностях  и напряжений на емкостях
и напряжений на емкостях  в момент коммутации. В зависимости от начального энергетического состояния цепи различают два типа задач расчета переходных процессов: задачи с нулевыми начальными условиями, когда непосредственно в момент коммутации
в момент коммутации. В зависимости от начального энергетического состояния цепи различают два типа задач расчета переходных процессов: задачи с нулевыми начальными условиями, когда непосредственно в момент коммутации 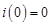 ,
, 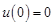 ; и задачи с ненулевыми начальными условиями, когда
; и задачи с ненулевыми начальными условиями, когда  и (или)
и (или)  .
.
Нулевые и ненулевые значения начальных условий для тока в катушке индуктивности  и напряжения на конденсаторе
и напряжения на конденсаторе  называются независимыми. Для определения независимых начальных условий в цепи до коммутации (
называются независимыми. Для определения независимых начальных условий в цепи до коммутации ( ) любым известным способом рассчитываем токи в индуктивностях и напряжения на емкостях. Согласно законам коммутации полученные значения и будут являться независимыми начальными условиями. Начальные условия остальных токов и напряжений называются зависимыми. Чтобы определить их, для цепи, образованной после коммутации, составляют уравнения Кирхгофа и записывают эти уравнения для момента коммутации
) любым известным способом рассчитываем токи в индуктивностях и напряжения на емкостях. Согласно законам коммутации полученные значения и будут являться независимыми начальными условиями. Начальные условия остальных токов и напряжений называются зависимыми. Чтобы определить их, для цепи, образованной после коммутации, составляют уравнения Кирхгофа и записывают эти уравнения для момента коммутации  с учетом законов коммутации. Полученную систему алгебраических уравнений решают относительно искомых величин при
с учетом законов коммутации. Полученную систему алгебраических уравнений решают относительно искомых величин при  .
.
Если число корней характеристического уравнения больше одного, то необходимо иметь не только начальные условия искомой переменной, но и ее производных. При этом порядок производных, начальное значение которых необходимо знать, на единицу меньше числа корней характеристического уравнения. Для определения производных при  уравнения Кирхгофа дифференцируют и решают совместно для
уравнения Кирхгофа дифференцируют и решают совместно для  .
.
Данный метод применяют для решения дифференциальных уравнений первого и второго порядка. При более высоких порядках определение постоянных интегрирования и решение характеристического уравнения представляет собой сложный процесс.
2.2. Пример расчета цепи.
Рассмотрим схему, приведенную на рис. 2. Решим задачу, в которой в момент времени  происходит замыкание ключа в ветви источника. Параметры элементов:
происходит замыкание ключа в ветви источника. Параметры элементов: 
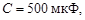


 .
.

Рис. 2
На основании законов Кирхгофа составим систему уравнений относительно мгновенных значений токов и напряжений для послекоммутационной схемы.

Представляем токи в виде суммы установившейся и переходной (свободной) составляющей:
 ,
,  ,
,  .
.
Принужденная (установившиеся) составляющая является частным решением неоднородной системы и определяет токи при достаточно больших  , когда переходные процессы закончились. Свободные составляющие являются общим решением однородной системы:
, когда переходные процессы закончились. Свободные составляющие являются общим решением однородной системы:

Представим систему следующим образом:


 .
.
Уравнение  является характеристическим уравнением. Имеем
является характеристическим уравнением. Имеем

 (5)
(5)
Подставляя конкретные числовые значения параметров в (5), получаем следующие уравнение
 ,
,
откуда  .
.
Корни получились разные и действительные. Ищем решение для свободных составляющих тока на катушке индуктивности и напряжения на конденсаторе в виде:
 ,
,  .
.
Определим начальные условия. Значения  и
и  в соответствии с законами коммутации определяются из докоммутационной схемы. Поскольку первая ветвь (содержащая источник) в докоммутационной схеме разомкнута
в соответствии с законами коммутации определяются из докоммутационной схемы. Поскольку первая ветвь (содержащая источник) в докоммутационной схеме разомкнута  . Напряжение на конденсаторе тоже равно нулю, поскольку, получается, что источников в схеме нет, а обкладки конденсатора замкнуты через резистор
. Напряжение на конденсаторе тоже равно нулю, поскольку, получается, что источников в схеме нет, а обкладки конденсатора замкнуты через резистор  , поэтому
, поэтому  . Найдем теперь значения производных этих функций в нулевой момент времени, исходя из системы уравнений, составленной по законам Кирхгофа для
. Найдем теперь значения производных этих функций в нулевой момент времени, исходя из системы уравнений, составленной по законам Кирхгофа для  .
.

получим  .
.
Определим принужденную (установившуюся) составляющую исходя из послекоммутационной схемы. В схеме действует источник постоянного напряжения. При постоянных токах сопротивление катушки индуктивности равно нулю, а сопротивление конденсатора бесконечно (разрыв ветви). Таким образом, послекоммутационная схема имеет вид:

Рис. 3. К определению установившихся составляющих переходных процессов электрической цепи
Определяем принужденные (установившиеся) составляющие:
 .
.
Исходя из начальных условий. Составим систему уравнений для определения постоянных интегрирования.


Решая эту систему, находим  .
.

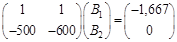 ,
,
отсюда находим  .
.
Таким образом,
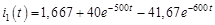 ,
,
 ,
,
 .
.
Далее можно найти соответствующие напряжения:



Из  найдем
найдем  . Графики найденных токов и напряжений приведены на рис. 4, 5.
. Графики найденных токов и напряжений приведены на рис. 4, 5.

Рис. 4. Переходные токи в цепи

Рис. 5. Переходные напряжения в цепи
3. Операторный метод расчета переходных процессов.
3.1.Операторное изображение функций, их производных и интегралов.
При использовании операторного метода действительные функции времени, называемые оригиналами, заменяются операторными изображениями. Соответствие между оригиналом и изображением устанавливается с помощью некоторого функционального преобразования. Это преобразование выбирается так, чтобы операции интегрирования и дифференцирования оригиналов заменялись алгебраическими операциями над их изображениями. В этом случае дифференциальные уравнения для оригиналов переводят в алгебраические для их изображений.
Связь между оригиналом  и его изображением устанавливается с помощью интеграла Лапласа:
и его изображением устанавливается с помощью интеграла Лапласа:
 , (6)
, (6)
где  – комплексное число.
– комплексное число.
 Операторное изображение действительной функции
Операторное изображение действительной функции  является функцией комплексного числа
является функцией комплексного числа  . Часто интеграл (1.4) называют интегралом Лапласа.
. Часто интеграл (1.4) называют интегралом Лапласа.
Для того чтобы интеграл Лапласа имел конечное значение, функция  должна удовлетворять определенным условиям. Она должна удовлетворять условиям Дирихле: за любой конечный промежуток времени иметь конечное число разрывов первого рода и конечное число максимумов и минимумов. Кроме того, будем считать, что при
должна удовлетворять определенным условиям. Она должна удовлетворять условиям Дирихле: за любой конечный промежуток времени иметь конечное число разрывов первого рода и конечное число максимумов и минимумов. Кроме того, будем считать, что при  удовлетворяется условие:
удовлетворяется условие:  , где A и a – некоторые положительные числа. Все реальные токи и напряжения удовлетворяют этим условиям. Для того чтобы интеграл Лапласа имел конечное значение, необходимо полагать
, где A и a – некоторые положительные числа. Все реальные токи и напряжения удовлетворяют этим условиям. Для того чтобы интеграл Лапласа имел конечное значение, необходимо полагать  .
.
Условимся записывать преобразование Лапласа в виде
 .
.
Соответствие между оригиналом и изображением
 .
.
По определению, преобразование Лапласа применимо с момента  . Обозначая значение функции и ее производных
. Обозначая значение функции и ее производных  и т.д., будем понимать под ними их значение при
и т.д., будем понимать под ними их значение при  .
.
Существует обратное функциональное преобразование Лапласа, по которому можно определить оригинал, зная его изображение. Его называют обратным преобразованием Лапласа:
 , (7)
, (7)
где  .
.
Обратное преобразование Лапласа кратко записывается в виде
 .
.
Соответствие некоторых характерных функций и их изображений приведено в таблице 2. Более полно таблицы соответствия оригиналов и изображений приведены в соответствующих справочниках [1].
Достоинством преобразования по Лапласу является его соответствие с преобразованием Фурье, на котором основывается широко используемый в настоящее время частотный метод анализа цепей.
Таблица 2
Соответствие некоторых оригиналов и их изображений по Лапласу
| Оригинал | Изображение |

| 
|

| 
|

| 
|

| 
|

| 
|
| 
|

| 
|

| 
|
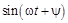
| 
|

| 
|

| 
|

| 
|
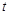
| 
|

| 
|

| 
|

| 
|
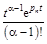
| 
|
Интегралу Лапласа (6) присущи следующие свойства:
1. Линейность:
 (8)
(8)
где 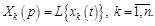
2. Изображение производной
 . (9)
. (9)
Изображение второй производной
 .
.
Изображение производной n -го порядка
 .
.
При нулевых начальных значениях
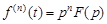 .
.
3. Изображение от интеграла
 . (10)
. (10)
В дифференциальных уравнениях электрических цепей с производной во времени чаще всего встречаемся в напряжении на катушке:  . Операторное изображение для
. Операторное изображение для 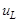
 .
.
С интегралом чаще всего встречаемся в выражении напряжения на конденсаторе:  .
.
Изображение по Лапласу
 ,
,
где  – изображение постоянной величины
– изображение постоянной величины  .
.
Таким образом, при составлении уравнений цепи в операторной форме автоматически будут учитываться физические начальные условия – значения токов в катушках и напряжений на конденсаторах при  .
.
4. Смещение в действительной областина величину  :
:
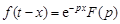 .
.
5. Смещение в комплексной области на число a
 .
.
