Голоморфные (аналитические) функции
Предварительно следует прочитать п.. из [1].
Пусть G и D – области на комплексной плоскости и 
– отображение из 
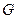в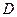 
(
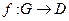). Говорят, что функция дифференцируема в точке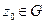 
, если существует число 
такое, что приращение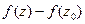 
функции можно представить в виде
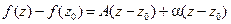
для всех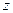 
из некоторой окрестности точки 
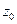, где бесконечно малая функция 
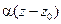имеет в точке 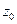более высокий порядка малости, чем 
, то есть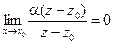 
. Если дифференцируема в точке 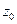, то, как и в случае функций действительного переменного, является производной функции в точке и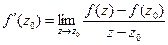 
.
Для того, чтобы функция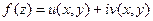 
была дифференцируема в точке 
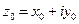необходимо и достаточно, чтобы выполнялись условия Коши-Римана
Говорят, что функция голоморфная (аналитическая) в точке 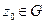, если она дифференцируема в точке 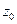и в некоторой окрестности точки 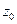и производная непрерывна в точке .
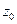Модуль производной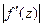 
есть коэффициент линейного растяжения при отображении в точке 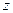, а аргумент производной 
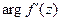равен углу поворота при отображении любого направления исходящего из точки .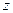
Функция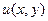 
называется гармонической, если она удовлетворяет уравнению Лапласа 
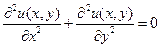. Действительная и мнимая части голоморфной (аналитической) функции являются гармоническими функциями.
1.4.1. Выяснить, где голоморфна функция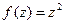 
.
Так как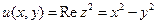 
, 
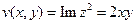, то получаем 
, 
, 
, 
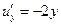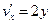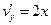. Условия Коши-Римана выполнены во всех точках комплексной плоскости, поэтому функция аналитическая (голоморфная) во всей комплексной плоскости.
1.4.2. Выяснить, где голоморфна функция 
.
Так как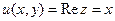 
, 
, то получаем 
, 
, 
, 
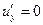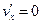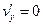. Условия Коши-Римана не выполнены ни в одной точке комплексной плоскости, поэтому функция не является аналитической (голоморфной) ни в одной точке комплексной плоскости.
1.4.3. Какая часть комплексной плоскости сжимается и какая растягивается при отображении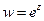 
?
Плоскость растягивается, когда коэффициент линейного растяжения больше единицы и сжимается, когда этот коэффициент больше нуля и меньше единицы. Коэффициент линейного растяжения функции имеющей производную равен модулю производной. Так как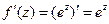 
, то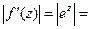 
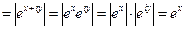. Следовательно, точки в которых плоскость растягивается, удовлетворяют неравенству 
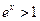, откуда получаем 
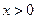, или, что тоже самое, 
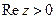. Аналогично показывается, что плоскость сжимается при 
.
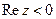1.4.4. Для отображения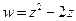 
найти точки, в которых коэффициент линейного растяжения равен 0.
Имеем 
, 
. Следовательно 
, откуда получаем 
. (Физический смысл).
1.4.5. Для отображения 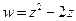найти точки, в которых угол поворота равен 0.
Так как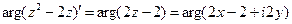 
, то
Приравнивая аргумент к нулю, получаем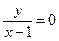 
. Поэтому угол поворота любого направления равен нулю на оси 
1.4.6. Восстановить голоморфную (аналитическую) функцию, если
а)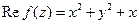 
.
Проверяем, является ли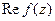 
гармонической функцией. Имеем 
, 
, 
, 
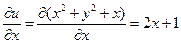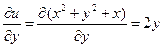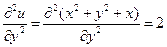. Поэтому 
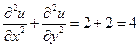. Следовательно, функция 
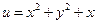не является гармонической и не может быть действительной частью голоморфной (аналитической) функции.
б)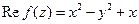 
.
Проверяем, является ли 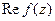гармонической функцией. Имеем 
, 
, 
, 
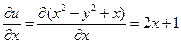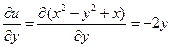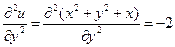. Поэтому 
. Следовательно, функция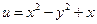 
гармоническая и может быть действительной частью голоморфной (аналитической) функции.
Далее,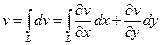 
. Используя условия Коши-Римана, можем это соотношение переписать в виде 
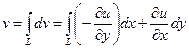. Так как криволинейный интеграл не зависит от пути интегрирования, то получаем, с точностью до константы, 
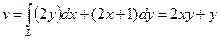. Таким образом,
.
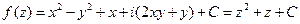