Разложение элементарных функций в ряд Маклорена.

Билет1

1)Двойной интеграл: Предел интегральных сумм (1) при l → 0 называется двойным интегралом и обозначается или

Площадь пластинки

Объём тела

Масса

Пусть γ(x,y,z) -- плотность тела V в точке (x,y,z). Тогда его масса M равна

Пусть γ (x,y) -- поверхностная плотность пластинки D в точке (x,y). Тогда её масса M равна

 

Пусть тело V задано так

Тогда объём этого тела равен .

Необходимое условие интегрируемости. Если функция интегрируема на отрезке, то она ограничена на нем.

Свойство 1. Двойной интеграл суммы двух функций равен сумме двойных интегралов.

Свойство 2. Постоянный множитель можно выносить за знак двойного интеграла.

Свойство 3 (аддитивность)} Если область D разбить на две области D_1 и D_2 так, что пересечение D_1∩ D_2 -- кривая, то ∬_D=∬_{D_1}+∬_{D_2}.

Оценки интегралов

 

1. Если то

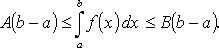
Теорема о среднем Если f непрерывна на [a,b], то

2) дробно-линейной Функция вида , где a,b,c,d∈ℂ и ad-bc≠ 0,

Инверсия

Преобразование евклидовой плоскости, переводящее всякую точку P, не совпадающую с O в инверсную точку P', называется инверсией. Рассмотрим лишь случай, когда P лежит вне круга. Проводим касательную к окружности γ из точки P. Пусть A -- точка касания. Опускаем перпендикуляр из точки A на луч OP. Инверсная точка P' будет основанием этого перпендикуляра. Это следует из подобия треугольников OAP' и OAP:

OA/ OP= OP'/OA, откуда R²=OA²=OP⋅OP'.

При инверсии центр круга переходит в бесконечно удаленную точку. Наоборот, если P→ ∞, то P'→ O.

Теорема [круговое свойство] Всякая дробно-линейная функция переводит окружность в расширенном смысле в окружность в расширенном смысле.

Предложение 1. Дробно-линейная функция, отображающая верхнюю полуплоскость на внутренность единичного круга имеет вид

Предложение 2. При любом дейсвительном и любом комплексном α, не принадлежащем единичной окружности, дробно-линейная функция следующего вида:

отображает единичную окружность на себя. Если , то (3) отображает единичный круг на себя, а при (3) отображает единичный круг на внешность единичного круга.

Предложение 3. Группа дробно-линейных преобразований, оставляющих верхнююполуплоскось на месте, состоит из функций вида

 

Билет 2

1)Поставим задачу -- найти массу нити L, заданной параметрически x=x(t), y=y(t), z=z(t), еслиa≤ t≤b и имеющей линейную плотность γ(x,y,z). Дифференциал массы находится так

dM=γdl=γ(x,y,z)\sqrt{d^2x=d^2y=d^2z}=γ(x(t),y(t),z(t))\sqrt{x'^2+y'^2+z'^2}dt

Отсюда получаем ответ

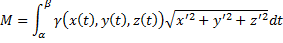
Пустьa=t_0<t_1<...<t_n=b -- разбиение, ξ _i\in[t_{i-1},t_i] -- отмеченныеточки.ОбозначимΔ s_i=\sqrt{(x(t_i)-x(t_{i-1}))^2+(y(t_i)-y(t_{i-1}))^2+(z(t_i)-z(t_{i-1}))^2}Тогда, поопределениюкриволинейныйинтегралподлинедугиэто

Свойства как у обычного интеграла.

Имеется кривая L в пространстве с началом M и концом N и векторное поле F на L. Разобьём L точкамиM=M_0,M_1,...,M_n=N. Параметром этого разбиения} lназовём величину max_i{| ΔS _i|}. Обозначим \DeltaS _i=\ar{M_iM_{i+1}}. Составим интегральную сумму}

\sum_i F _i \Delta S _i (1)

Криволинейныминтеграломполя F покривойL(обозначается )называетсяпредел интегральных сумм (1), если l→0.

Замечание. Криволинейный интеграл -- работа силового поля F по перемещению материальной точки вдоль L.

Пусть F =X(x,y,z)\bi+Y(x,y,z)\bj+Z(x,y,z)\bkиM_i(x_i,y_i,z_i). Тогда

\Delta S _i=Δ x_i\bi+Δy_i\bj+Δz_i\bkи

\sum_i F _i ΔS _i=\sum_i (X(x_i,y_i,z_i)Δx_i+Y(x_i,y_i,z_i)Δy_i+ Z(x_i,y_i,z_i)Δz_i

Поэтому

В случае замкнутой кривой L, т.е. когда M=N, криволинейныйинтеграл обозначают и назавают циркуляцией векторного поля F по замкнутому контуру L

2)

Ряд вида

называется функциональным. Областью сходимости этого ряда называется множество всех чисел при которых числовой ряд сходится.

Функциональный ряд вида

называется степенным рядом.

Теорема Абеля. Если ряд (1) сходится при некоторомзначении , то он сходится абсолютно при любом значении таком, что . Если же ряд (1) расходится при , то онрасходится при любом модуль которого больше чем .

Следствие. Существует число или такое, что степенной ряд (1) сходится абсолютно при и расходится при .

Число R, о существовании которого говорится в следствии, называется радиусом сходимости степенного ряда (1).

Радиус сходимости можно вычислить по одной из следующих двухформул (при условии, что пределы существуют)

 

Определение 1. Если ряд (1) сходится к функции f(x) вокрестности точки a, то функцию называют аналитическойв этой точке. Аналитичность функции на множествеозначаетаналитичность в каждой точке этого множества.

 

 

Билет 3

1)Суммаряда

Определение суммы ряда.

Выражение вида

называем рядом; -- n-ый член ряда (1). Сумма называется n-ой частичной суммой ряда (1).

Определение 1. Суммой ряда (1) называется предел частичныхсумм, если . Итак, суммаряда (1) есть число

т.е. такое число, что для любого найдется натуральное начиная с которого, т.е. для любого выполняется неравенство

Если существует предел (2), то ряд (1) называется сходящимся. В противном случае, ряд (1) называется расходящимся.

Необходимый признак сходимости.

Теорема. Если ряд (1) сходится то n-ый член стремится к 0.

Доказательство. . □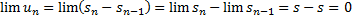

Пример. Гармоническим рядом называется ряд

Для этого ряда но этот ряд расходится, как показывает далее интегральный признак Коши.

Геометрическая прогрессия

- это ряд вида

Число q называется знаменателем геометрической прогрессии.

Теорема 2. Пусть . Тогда геометрическая прогрессия сходится тогда и только тогда, когда |q|<1. В этом случае сумма геометрической прогрессии равна .

Утверждение следует из равенства □

Арифметические операции с рядами.

Определим сумму двух рядов 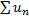и как ряд с n-ым слагаемым . Произведение ряда (1) на число l - это ряд .

Теорема. Если ряды 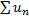и сходятся соответственно к s и t, то сумма этих рядов сходится к числуs+t, а произведение ряда 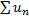на число l сходится к .

Доказательство вытекает из соответствующих свойств предела

2)

Поле комплексных чисел

Алгебраической причиной введения комплексных чисел является отсутствие действительного корня уравнения

Комплексное число имеет вид , где -- вещественные числа, называемые действительной и мнимой частью комплексного числа z (записываем так: 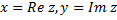), а -- новое число, называемое комплексной единицей и обладающее свойством . Два комплексных числа равны в том и только том случае, когда совпадают их действительные и мнимые части. Операции сложения и умножения над комплексными числами определяются следующим образом

Заметим, что в этих равенствах знаки сложения и умножения использованы в двух смыслах: как сложение (умножение) действительных чисел 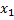и и как сложение (умножение) двух комплексных числе и согласно определению (1).

Если то либо , либо , и поэтому . В этом случае комплексное число имеет обратное

Действительно,

Тем самым совокупность всех комплексных чисел превращается в поле. Поле действительных чисел изоморфно вкладывается в поле посредством отображения , как это уже было отмечено в равенствах (2).

iy

x

Комплексная плоскость.

Комплексные числа изображаютсяточками на плоскости Oxy или векторами с начальной точкой в начале координат (см. рис. 1). Горизонтальная ось Oxназывается действительной осью, а вертикальная ось Oy называется мнимой осью и обозначается как ибо по ней откладываются чисто мнимые числа и.т.д.. При этом сложение двух комплексных чисел можно рассматривать как сложение двух векторов по правилу параллелограмма

Сопряжение комплексных чисел

Комплексное число называется комплексно сопряженным к , а отображение называется сопряжением.Сопряжение является биективным отображением комплексной плоскости на себя. С геометрической точкизрения операция сопряжение есть не что иное, как отражение относительно действительной оси.

Равенство имеет место тогда и только тогда, когда z – действительноечисло. Кроме этого, сопряжение обладает свойством гомоморфности по отношению к сложению и умножению:

Эти свойства проверяются непосредственно. Как и всякая симметрия, сопряжение обладает свойством инволютивности: для любого .

Отметим также свойство

 

Билет 4

1)Абсолютная сходимость.

Дан ряд 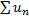с произвольными слагаемыми. Рассмотрим ряд

составленный из абсолютных величин членов исходного ряда.

Теорема. Если ряд (1) сходится, то и исходный ряд сходится.

Доказательство. Так как и ряд (1) сходится, то по тереме сравнения получаем сходимость ряда . Арифметические операции с рядами показывают, что сходится ряд 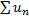равный разности сходящихся рядов и . □

Определение. Ряд 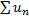такой, что ряд (1), составленный из абсолютных величин сходится, называется абсолютно сходящимся. Если же ряд (1) расходится, а сам ряд 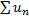сходится, то ряд 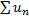называют условно сходящимся.

2)

Тригонометрическая форма записи комплексных чисел

Изобразим комплексное число вектором. Длина этого вектора, т.е. величина называется модулем комплексногочисла и обозначается . Если -- действительное число, то приходим к «школьному» модулю, ибо . Если , то угол, который образует вектор с действительной осью называется аргументом комплексного числа и обозначается Пусть – модульи аргумент ненулевого комплексного числа. Тогда

(1)

Выражение называется тригонометрической формой записи комплексного числа.

Комплексная экспонента

Правило (2) предыдущего параграфа дает нам право определить экспоненту чисто мнимого числа:

Действительно, таким образом определенная функция обладает следующими свойствами:

Применяя тригонометрические формулы «косинус суммы» и «синус суммы», приходим к следующему правилу: при перемножении комплексных чисел модули умножаются, а аргументы складываются

(2)

В частности, перемножая число на себя nраз, получаем формулу Муавра:

Билет 5

1)РядыТейлораиМаклорена

ВспомнимформулуТейлора:

Пусть здесь -- бесконечно дифференцируемая функция. Тогдастепеннойряд

называется рядом Тейлора функции в окрестности точки . В частном случае, когда , этот ряд называют рядомМаклорена.

Разложение элементарных функций в ряд Маклорена.