Изучение колебательного движения.
F
Mg
x
M
D l
x
Груз на пружине
Равновесное положение груза массы M, подвешенного на пружине (см. рис. 1), определяется равенством величин силы упругости F = k.D l и силы тяжести Mg
k.D l = Mg, (1)
где k – коэффициент упругости (жесткость) пружины, D l – ее удлинение от недеформированного состояния. Выведенный из положения равновесия груз колеблется около этого положения по синусоидальному (гармоническому) закону x = A. cos(wt+j), (2)
|
в момент
времени t = 0. Другими словами, A и j определяются способом возбуждения колебаний груза.
Гармоническая зависимость x(t) вида (2) является, как можно проверить непосредственной подстановкой, решением уравнения 
, (3)
называемого уравнением гармонического осциллятора. Кроме груза на пружине, гармоническими осцилляторами являются, например, математический маятник, электрический колебательный контур без потерь и ряд других систем.
В нашем случае уравнение (3) можно получить из второго закона Ньютона, который в проекции на ось x (см. рис. 1) имеет вид 
. (4)
Деформация пружины в произвольном положении груза равна x+D l (x+D l < 0 соответствует сжатой пружине), и проекция силы, действующей на груз со стороны пружины, равна
Fx = -k. (x+D l). Если, кроме того, учесть условие (1) и равенство 
, то после преобразований получается уравнение гармонического осциллятора
, (3’)
Сравнение (3) и (3’) показывает, что w2 = k/M, а период колебаний
. (5)
Формула (5) справедлива, если масса пружины m<<M (учет массы пружины см. в Приложении).
Задание
1. Определите k из формулы (1), измеряя для каждой пружины величины D l с различными грузами массами M.
2. Измерьте периоды колебаний для каждой пружины с различными грузами M. Постройте графики зависимости T2 от M. Сравните с расчетной зависимостью 
.
3. Выясните зависимость периода колебаний от амплитуды.
4. Изучите зависимость амплитуды колебаний от времени. Для этого измерьте, не останавливая колебаний (на ходу), через какое время амплитуда станет равной ¾ от начального значения А0, затем ½ А0, ¼ А0. Постройте график зависимости А от t.
Замечания: а). При определении k положение недеформированной пружины иногда трудно зафиксировать из-за неровности пружины, которая не висит строго по вертикальной линии. В этом случае надо подвесить начальный груз и от этого положения вести отсчет D l под действием других грузов.
б). Для приведения груза в движение поднимайте его из положения равновесия вверх. Это предохраняет грузы от падения и дает более правильное направление колебаниям.
Вопросы:
1. 
Что вы можете сказать о величине и направлении скорости и ускорения груза в следующих трех положениях груза (см. рис. 2): а) крайнее верхнее положение, б) переход через положение равновесия, в) крайнее нижнее положение?
2. Какие превращения энергии происходят при колебаниях груза?
3. Как изменится период колебаний, если, отрезав часть пружины, сделать ее короче?
4. Получите уравнение гармонического осциллятора для груза на пружине из закона сохранения механической энергии (таким способом уравнение (3) получено в Приложении).
5. Найдите А и j в законе движения груза (2) в трех различных случаях возбуждения колебаний: груз отпущен с высоты на h выше положения недеформированной пружины, на h ниже того же положения, груз в положении равновесия получил скорость V0.
6. Как будет зависеть период колебаний от амплитуды, если при достаточно больших амплитудах закон Гука нарушается?
Приложение. Учет влияния массы пружины на период колебаний груза.
В лабораторной установке груз колеблется на вертикально расположенной пружине. В области линейных деформаций (когда справедлив закон Гука) сила тяжести не влияет на период колебаний, поэтому для упрощения анализа рассматривается горизонтальная ориентация пружины (см. рис. 3). При колебаниях смещение какого-либо витка пружины тем больше, чем далее он отстоит от закрепленного конца пружины. В приближении однородной деформации смещение витка и, следовательно, его скорость прямо пропорциональны равновесной (при недеформированной пружине) координате витка z. Идеальная пружина (ее масса пренебрежимо мала) всегда деформируется однородно. Для реальной пружины такая идеализация тем точнее, чем меньше масса пружины по сравнению с массой груза. Уравнение гармонического осциллятора для нашей системы можно получить из закона сохранения энергии. Потенциальная энергия деформированной пружины в нашем приближении имеет обычный вид
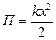, (П.1)
где х – удлинение пружины, равное смещению груза из положения равновесия. Кинетическая энергия груза равна
, (П.2)
где – скорость груза, равная скорости правого конца пружины. В приближении однородной деформации скорость кусочка пружины dz массы dm = m.dz/ l равна z.Vx/ l (l – равновесная длина пружины, m – ее масса), а его кинетическая энергия равна
dKП = mVx2. z2dz / (2 l 3). Кинетическая энергия всей пружины найдется интегрированием
, (П.3)
Механическая энергия системы при пренебрежении трением должна оставаться постоянной, т.е. сумма П, КГ и КП постоянна:
. (П.4)
После дифференцирования равенства (П.4) по времени и некоторых преобразований получается уравнение гармонического осциллятора
. (П.5)
Сравнение (П.5) с (3) дает 
и 
. (П.6)
Таким образом, масса m пружины влияет на период колебаний груза так же, как влиял бы дополнительный груз массы m/3, подвешенный вместе с грузом M на невесомую пружину той же жесткости.