ШЕСТИЗВЕННОГО РЫЧАЖНОГО МЕХАНИЗМА.

Лист 1. КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ

 

Известны (заданы):

1. Кинематическая схема шестизвенного рычажного механизма

2. Длины звеньев L_ОА, L_АB, L_BD, координаты неподвижных точек Х_С, Y_C, Y_D, и углы направляющих (если они содержатся в задании).

3. Частота вращения вала двигателя n_ДВ, об/мин.

Требуется:

1. Графическим методом определить законы перемещений, скоростей и ускорений выходного звена.

2. Построить планы скоростей для 12 положений механизма.

3. Построить планы ускорений для позиции механизма, в которой сила полезных сопротивлений Р_ПС, развиваемая выходным звеном, имеет максимальное значение (см. график Р_ПС в задании [1]).

 

ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ

 

1.1.Определение законов перемещений, скоростей и ускорений выходного звена графическим методом

Последовательность решения рассмотрим на примере механизма, изображенного на рис. 1.

Строятся несколько (желательно 8 или 12) совмещенных планов механизма в произвольно выбранном масштабе длин:

М_L = L_ОА/ОА, мм,

где: L_ОА – заданная длина кривошипа в метрах,

ОА – длина отрезка, мм, изображающего кривошип на плане механизма.

Величина ОА берется произвольно в пределах 20…50 мм. При этом следует учитывать, чтобы, во-первых, масштаб М_L был удобен для расчетов (желательно круглое число), во-вторых, чтобы план механизма разместился на отведенном для него месте чертежа.

Все линейные размеры других звеньев и координаты неподвижных точек переводятся этим масштабом в отрезки:

х_С = Х_С/М_L; y_D = Y_D/М_L; y_С = Y_C/М_L; BD = L_BD/M_L, мм.

Построение совмещенного плана механизма начинается с построения траектории движения точки А кривошипа. Для этого проводится окружность радиусом ОА с центром О, которая делится на 8 или 12 равных частей. Наносятся координаты неподвижных точек С и Y_D.

Затем методом засечек строятся положения подвижных точек (в нашем примере – точек В и D).

Строится график перемещения выходного звена – точки D в координатных осях перемещения S_D и времени t (рис. 2).

Для удобства желательно масштаб перемещения Мs принять равным масштабу длины: M_S = M_L.

На оси t откладываются в мм 12 равных отрезков; рекомендуется принять L_X = 180 мм, этот отрезок будет изображать время одного оборота кривошипа в масштабе:

M_t = T/L_X,

где Т - время (период) одного оборота.

Величина периода Т вычисляется по формуле

Т = 2^.p/W₁, с,

а угловая скорость вращения кривошипа – по формуле

W₁ = p^. n_ДВ/(30 ^. U_1-H),

где n_ДВ - заданная частота вращения вала двигателя, об/мин;

U_1-H – заданное передаточное отношение зубчатого механизма.

Окончательная формула расчета масштаба времени:

 

M_t = (60^. U_1-H)/(L_X ^. n_ДВ), c/мм.

 

Приняв положение 1 кривошипа, соответствующее крайнему левому положению ползуна (точки Д), из точек 2,3 и т.д., расположенных на оси t, откладывают ординаты, равные величине перемещения ползуна от крайнего левого положения, взятые с совмещенного плана механизма. Полученные точки обводят плавной кривой. Отрезок H_Д – это максимальный ход ползуна – точки Д.

Строится график скорости точки Д (рис.3) путем графического дифференцирования графика S_D (так как V_D = dS_D/dt). Оси абсцисс (времени t) на этих графиках одинаковы. Вычисляется масштаб графика скорости:

M_V = M_S/(M_t ^. h_v), м/с/мм,

где h_V – полюсное расстояние для дифференцирования (выбирается произвольной величины в пределах 20…40 мм, при этом следует учесть, что с увеличением h_V возрастает размер графика скорости по оси ординат).

При графическом дифференцировании методом хорд из полюса Р_V проводят лучи, параллельные хордам графика S_D, до пересечения с осью V_D. Полученные точки пересечения сносят на середины соответствующих участков и соединяют их плавной кривой.

Строится график ускорения точки Д (рис.4) путем графического дифференцирования графика V_D.Масштаб графика ускорений вычисляется по формуле:

M_A= M_V/(M_t ^. h_a), м/с²/мм,

где h_a = 20...40 мм - полюсное расстояние для дифференцирования, выбирается произвольно.

Дифференцирование можно проводить методом хорд или методом касательных. Для повышения точности построений желательно использовать оба метода.

 

1.2. Построение планов скоростей механизма

 

Рассмотрим пример для одного положения механизма. Для этого строим план механизма в заданном положении и в выбранном масштабе длин М_L (рис.5).

 

 

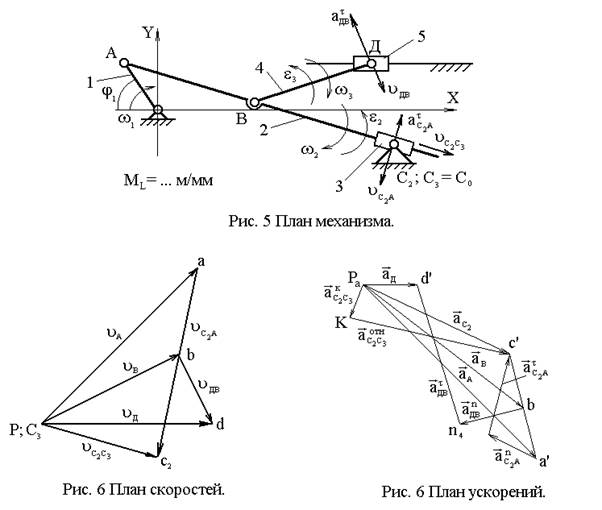
Вычисляется скорость точки А кривошипа:

V_A = W₁ ^. L_OA,м/с.

Вектор скорости V_A направлен перпендикулярно прямой ОА (кривошипа) в сторону вращения кривошипа.

Скорость V_C2 точки С звена 2 определяется графическим построением следующих векторных уравнений (т.е. построением планов скоростей):

V _C2 = V _A + V _C2A;

V _C2 = V _C3 + V _C2C3.

Здесь вектор скорости V _C2A направлен перпендикулярно прямой AC₂, но пока неизвестна величина этой скорости; скорость V _C3 = 0; вектор скорости V _C2C3 направлен параллельно прямой AC₂, но величина этой скорости также пока неизвестна.

Для определения неизвестных величин скоростей строим план скоростей в следующей последовательности. Из произвольно выбранной точки – так называемого полюса Р_V – перпендикулярно ОА проводится отрезок Р_Va произвольной длины (рис.6). Тогда масштаб плана скоростей вычисляется по формуле

M_V = V_A/Р_Va, м/с/мм,

где Р_Va - длина отрезка, мм, изображающая на плане скоростей вектор скорости V_A.

Из точки a перпендикулярно прямой АС₂ проводится луч. Через полюс Р_V проводится второй луч параллельно прямой АС₂. В месте их пересечения получаем точку с₂. Вектор Р_Vс₂ изображает скорость V _C2, а вектор ас₂ – скорость V _C2A. Вычисляются величины скоростей по формулам

V _C2 = (Р_Vс₂) ^. M _V;

V _C2A = (ас₂) ^. M _V, м/с.

Здесь длины отрезков Р_Vс₂ и ас₂ взяты из плана скоростей. Вычисляем угловую скорость кулисы 2:

W₂ = V_C2A/L_AC2, 1/с.

Здесь L_AC2 = (AC₂) ^. M_L, м, а величина АС₂ в мм берется из плана механизма.

Определяется скорость точки В, принадлежащей кулисе 2. Для этого используется теорема подобия: Отрезки относительных скоростей на плане скоростей образуют фигуру, подобную соответствующей фигуре на плане механизма.

В соответствии с ней составляется уравнение пропорции

АС₂/ас₂ = AB/ab.

Здесь длины отрезков АС₂ и АВ берутся в мм из плана механизма, а длина отрезка ас₂ – из плана скоростей. Вычисляется длина отрезка ab и откладывается на отрезке ас₂ плана скоростей. Полученный вектор (Р_vb) изображает на плане скоростей скорость V _B точки В, причем величина скорости точки В вычисляется по формуле

V _B = (Р_vb) ^. M _V, м/с.

Определяется скорость точки Д. Для этого составляется векторное уравнение скорости звена 4:

V _D = V _B + V _DB.

Здесь скорость V _B уже известна как по величине, так и по направлению, а V _DB^BD и вектор V _D параллелен движению ползуна 5. Для нахождения величин V _DB и V _D строится план скоростей звена 4 в следующей последовательности. Через точку b плана скоростей проводится линия, перпендикулярная прямой ВD плана механизма, а через полюс Р_V – прямая, параллельная движению ползуна 5. В месте их пересечения получается точка d. Вычисляются значения скоростей:

V_DB = (bd) ^. M_V,

V_D = (Р_Vd) ^. M_V, м/с.

Направления векторов скоростей устанавливаются в соответствии с векторным уравнением скоростей.

Далее вычисляется угловая скорость шатуна:

W₄ = V_DB/L_BD, 1/с.

Направления угловых скоростей звеньев W ₂ и W ₄ показываются на плане механизма. Планы скоростей строятся для всех 12 позиций. С их использованием вычисляются линейные скорости всех характерных точек механизма (центров кинематических пар, центров масс звеньев и т.д.), угловые скорости звеньев. Результаты расчетов удобно свести в таблицу. Вычисленные скорости нужны в дальнейшем для проведения динамического анализа механизма и расчета маховика (см. лист 4 курсового проекта).

 

1.3. Построение плана ускорений механизма

 

Сначала строится план механизма в выбранном масштабе длин M_L и в той позиции, в которой сила полезных сопротивлений Р_ПС, приложенная к ползуну 5, максимальна. Это желательно сделать по следующим причинам: знание величин ускорений звеньев необходимо для расчета сил инерции и моментов сил инерции, а при проведении силового анализа механизма целесообразно рассматривать именно то положение механизма, которое нагружено максимальной силой Р_ПС. Для того чтобы его определить, необходимо на прямой H_D хода ползуна (смотри совмещенные планы механизма) построить график изменения силы P_ПС и определить искомую позицию механизма.

Ускорение точки А кривошипа определяется с использованием векторного уравнения ускорения точки А кривошипа относительно оси вращения О:

а _А = а _АО = а ⁿ_АО + а ^t_АО,

где а ⁿ_АО – нормальная составляющая ускорения точки А относительно О;

а ^t _АО - тангенциальная составляющая ускорения А относительно О.

Так как по условий задачи угловая скорость кривошипа постоянна (W₁ = const), то угловое ускорение e₁ = 0, а тангенциальная составляющая ускорения также равна нулю:

а^t_АО = e₁ ^. L_OA = 0.

Тогда полное ускорение точки А равно нормальной составляющей ускорения: а_А = аⁿ_АО, причем

аⁿ_АО = w²₁ ^. L_OA, м/с².

Вектор ускорения аⁿ_АО параллелен ОА и направлен от А к 0.

Затем определяется ускорение точки С₂, принадлежащей кулисе 2.

Для этого составляются следующие векторные уравнения ускорений:

а) для звена 2 (кулисы)

a _C2 = а _А + a ⁿ_C2А + a ^t_C2A;

б) для звена 3 (качающегося камня):

a _C2 = a _C3 + a ^k_C2C3 + a^ОТН_C2C3.

Рассчитываются величины ускорений, входящих в эти векторные уравнения:

нормальное ` a ⁿ_C2А = V ²_C2A/ L _AC2 , м/с²;

Кориолисово a ^k_C2С3 = 2 V _C2C3 ^. w ₂, м/c².

Причем`вектор нормального ускорения a ⁿ_C2А параллелен АС₂ и направлен от С₂ к A.

Для определения направления вектора Кориолисова ускорения a ^k_C2C3 нужно вектор С₂С₃ относительной скорости V _C2C3 повернуть на 90° по направлению угловой скорости w₂ кулисы. Вектор тангенциальной составляющей ускорения a ^t_C2A перпендикулярен АС₂, а вектор относительного (релятивного) ускорения a ^ОТН_C2C3 параллелен АС₂. Причем здесь имеется в виду, что нормальное ускорение a ⁿ_C2С3 = 0, если звено АС₂ – прямая линия.

Неизвестные величины a ^t_C2A и a ^ОТН_C2C3 находятся построением плана ускорений (рис.7). Для этого сначала выбирается масштаб плана ускорений:

М _а = a _А/(Р_аа ΄), м/с²/мм,

где (Р_аа ΄) - длина вектора в мм, изображающего ускорение а_А на плане ускорений.

Величина (Р_аа ΄) выбирается произвольно из расчета, чтобы масштаб был удобен для расчетов (желательно круглое число), а план ускорений разместился на отведенном месте чертежа. Построение плана ускорений осуществляется в соответствии с последовательностью написания вышеприведенных векторных уравнений.

Сначала строится (т.е. изображается графически) первое векторное уравнение, для чего из произвольно выбранного полюса Р_А (рис.7) параллельно отрезку ОА (см. план механизма) проводится вектор Р_аа с ранее выбранной длиной (см. расчет масштаба М _а). Он изображает ускорение а _А = а ⁿ_АО. Из точки a ΄ параллельно АС₂ проводится вектор (а΄n ₂), изображающий вектор a ⁿ_C2A. Длина вектора (a ΄ n ₂) вычисляется по формуле:

a ' n ₂ = a ⁿ_C2A/ М _а, мм.

Через точку n₂ проводится луч по направлению ускорения a ^t_C2A перпендикулярно АС₂.

Затем строится второе векторное уравнение. Из полюса Р_а проводится вектор (Р_аk) длиной Р_аk = a ^k_C2C3/ М _а, мм, изoбражающий Кориолисово ускорение a ^k_C2C3. Из точки К проводится луч по направлению ускорения a ^ОТН_C2C3, параллельный АС₂.

В месте пересечения лучей получается точка С₂', которую соединяют c полюсом Р_а и точкой а΄. Вектор n₂c₂΄ изображает ускорение a ^t_C2A, вектор (kC₂΄) – ускорение a ^ОТН_C2C3,а вектор(a'c'₂) – полное ускорение a _C2A.

Для определения ускорения точки В используется теорема подобия: отрезки относительных ускорений на плане ускорений образуют фигуру, подобную соответствующей фигуре на плане механизма.

В соответствии с ней составляется уравнение пропорции отрезков на плане механизма и плане ускорений:

(а'₂c'₂/АС₂) = (а'b'/AB),

откуда вычисляют длину отрезка

(а'b') = (а₂'c₂' ^. АВ)/АС₂, мм

и откладывают этот отрезок от точки а' в сторону точки с'₂ на плане ускорений. Соединив полюс Р_а с точкой b', получают полное ускорение точки В a_B, причем

a _B = (Р_а b') ^. М _а, м/с².

Определяют ускорение точки Д. Для этого составляется векторное уравнение ускорений шатуна 4

а _D = a _B + a ⁿ_DB + a ^t_DB.

Вычисляется величина нормального ускорения:

a ⁿ_DB = V ²_DB/ L _BD, м/с².

Из точки b΄ параллельно звену ВД откладывается вектор (b΄n₄) длиной b΄n₄ = a ⁿ_DB/М_А, мм, изображающий на плане ускорение a ⁿ_DB. Через точку n₄ проводится луч, перпендикулярный ДВ, до пересечения с проведенной из полюса Р_а прямой, параллельной движению ползуна 5. В месте пересечения получается точка d'. Вектор (Р_аd ') изображает полное ускорение точки Д – a_d, а вектор (n₄b') - тангенциальное ускорение a ^t_DB. Вычисляется величина этого ускорения

a ^t_DB = (n₄d ΄).

Вычисляются величины угловых ускорений звеньев 2 (кулисы) и 4 (шатуна):

e ₂ = a ^t_C2A/ L _AC2,1/с²;

e ₄ = a ^t_DB/ L _BD, 1/с².

Направления угловых ускорений определяются по тому, куда "вращают" векторы a ^t_C2A и a ^t_DB звенья 2 и 4, если их перенести соответственно в точки С₂ и Д плана механизма.

Для определения радиуса кривизны траектории движения точки В, совершающей сложное движение, используется формула

r = V²_B/aⁿ_B, м,

где V_B=(Р_Vb) ^. M_V, м/с - скорость точки В.

Для ее нахождения необходимо полное ускорение точки В разложить на нормальную и тангенциальную составляющие:

a _В = a ⁿ_B + a ^t_B.

Это можно сделать графически на построенном плане ускорений, причем нормальная составляющая ускорения точки В a ⁿ_B будет направлена перпендикулярно скорости V_B, а тангенциальная – a ^t_B – параллельно скорости V_B.