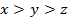В качестве множества элементарных исходов 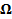 рассматривается какая-либо геометрическая фигура, имеющая меру, то есть длину, площадь или объем. В качестве
рассматривается какая-либо геометрическая фигура, имеющая меру, то есть длину, площадь или объем. В качестве  выступает совокупность измеримых подмножеств
выступает совокупность измеримых подмножеств 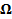 . Вероятностью события
. Вероятностью события 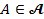 в этой модели полагают отношение мер множеств
в этой модели полагают отношение мер множеств  и
и 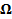 , то есть
, то есть 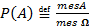 .
.
 Пример 7. На отрезок
Пример 7. На отрезок  длины
длины 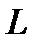 на числовой оси
на числовой оси  наудачу бросается точка
наудачу бросается точка  . С какой вероятностью расстояние от
. С какой вероятностью расстояние от  до ближайшего конца отрезка
до ближайшего конца отрезка  окажется больше
окажется больше  ?
?
Решение. Элементарным исходом в этом опыте будет число  . Рассмотрим рисунок 2, на котором благоприятные исходы заштрихованы. Тогда искомая вероятность равна отношению длины заштрихованного отрезка к длине всего отрезка
. Рассмотрим рисунок 2, на котором благоприятные исходы заштрихованы. Тогда искомая вероятность равна отношению длины заштрихованного отрезка к длине всего отрезка  . То есть
. То есть  .
.
Пример 8. Два человека договорились о встрече между 14.00 и 15.00. Каждый приходит в случайный момент времени из этого промежутка, ждет 15минут и уходит. С какой вероятностью встреча состоится?
 Решение. Элементарным исходом в этом опыте логично считать пару
Решение. Элементарным исходом в этом опыте логично считать пару  , где
, где 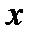 - время прихода первого человека, а
- время прихода первого человека, а 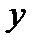 - время прихода второго. Будем считать, что
- время прихода второго. Будем считать, что 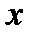 и
и  измеряются в минутах (после 14.00). Тогда
измеряются в минутах (после 14.00). Тогда  , а пара
, а пара 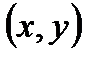 есть элемент декартова произведения
есть элемент декартова произведения 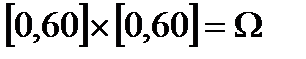 .
.
По условию встреча состоится, если 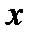 и
и  отличаются не больше, чем на 15 минут, то есть если
отличаются не больше, чем на 15 минут, то есть если 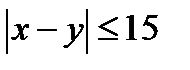 . На рисунке 3 эта область заштрихована.
. На рисунке 3 эта область заштрихована.
То есть, если пара 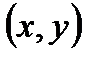 попадает внутрь заштрихованной области, то встреча состоится, а если вне области (на рисунке это точка (50,10)), то нет. Элементарный исход (50,10) означает, что второй приятель не дождется первого, поскольку пришел на 40 минут раньше. По условию все исходы
попадает внутрь заштрихованной области, то встреча состоится, а если вне области (на рисунке это точка (50,10)), то нет. Элементарный исход (50,10) означает, что второй приятель не дождется первого, поскольку пришел на 40 минут раньше. По условию все исходы  равновероятны, но поскольку их бесконечно много говорить о вероятности отдельного исхода не имеет смысла. Но можно говорить о вероятности попадания в какую-либо область, которая должна быть, очевидно, пропорциональна величине (мере) области. Мерой плоской области
равновероятны, но поскольку их бесконечно много говорить о вероятности отдельного исхода не имеет смысла. Но можно говорить о вероятности попадания в какую-либо область, которая должна быть, очевидно, пропорциональна величине (мере) области. Мерой плоской области  является площадь
является площадь 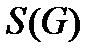 . В нашем случае
. В нашем случае 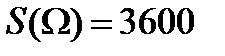 , а площадь заштрихованной части
, а площадь заштрихованной части  можно получить, вычитая площади двух прямоугольных треугольников (см. рисунок 3). Получаем
можно получить, вычитая площади двух прямоугольных треугольников (см. рисунок 3). Получаем  . Тогда доля благоприятных исходов равна
. Тогда доля благоприятных исходов равна  . Ее и естественно считать вероятностью встречи.
. Ее и естественно считать вероятностью встречи.
Пример 9. (игла Бюффона)(позже, если не знают интегралов)
На плоскость, разлинованную прямыми, параллельными оси  и отстоящими друг от друга на расстояние
и отстоящими друг от друга на расстояние 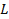 , наудачу бросается игла длины
, наудачу бросается игла длины 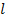 , (
, ( (см. рис.4). С какой вероятностью игла пересечет какую-либо линию?
(см. рис.4). С какой вероятностью игла пересечет какую-либо линию?
Решение. Пусть
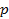
- расстояние от центра иглы до ближайшей прямой, а
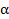
- угол между иглой и прямыми. Тогда
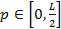
, а
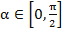
, причем считаем, что все эти значения равновозможны. Множеством элементарных исходов здесь будет прямоугольник, изображенный на рисунке 5. Выделим теперь благоприятные исходы.
В самом деле, игла пересечет одну из прямых, если  (см. заштрихованное множество на рисунке 5). Тогда искомая вероятность равна отношению площадей, то есть
(см. заштрихованное множество на рисунке 5). Тогда искомая вероятность равна отношению площадей, то есть
 .
.
Пример 10. Три раза запускается датчик случайных чисел, выбирающий числа из интервала  . Результатом этого опыта (элементарным исходом) можно считать тройку чисел
. Результатом этого опыта (элементарным исходом) можно считать тройку чисел 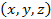 , то есть точку в кубе со стороной 1. Вероятность выбора точки из какой- либо части куба очевидно пропорциональна объему этой части. Поэтому применяем модель геометрических вероятностей. Рассмотрим события
, то есть точку в кубе со стороной 1. Вероятность выбора точки из какой- либо части куба очевидно пропорциональна объему этой части. Поэтому применяем модель геометрических вероятностей. Рассмотрим события  ,
,  и вычислим их вероятности.
и вычислим их вероятности.
Так как 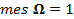 , то (см. рис. 6)
, то (см. рис. 6) 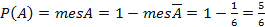
 Здесь
Здесь  находится и из геометрических соображений - это объем части куба над плоскостью
находится и из геометрических соображений - это объем части куба над плоскостью  (объем тетраэдра), который равен
(объем тетраэдра), который равен  .
.
Находим вероятность события  (см. рис. 7), она численно равна объему тетраэдра, ограниченного плоскостями:
(см. рис. 7), она численно равна объему тетраэдра, ограниченного плоскостями:  , следовательно,
, следовательно,  .
.
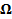 рассматривается какая-либо геометрическая фигура, имеющая меру, то есть длину, площадь или объем. В качестве
рассматривается какая-либо геометрическая фигура, имеющая меру, то есть длину, площадь или объем. В качестве  выступает совокупность измеримых подмножеств
выступает совокупность измеримых подмножеств 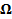 . Вероятностью события
. Вероятностью события 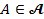 в этой модели полагают отношение мер множеств
в этой модели полагают отношение мер множеств  и
и 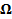 , то есть
, то есть 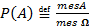 .
. Пример 7. На отрезок
 длины
длины 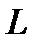 на числовой оси
на числовой оси  наудачу бросается точка
наудачу бросается точка  . С какой вероятностью расстояние от
. С какой вероятностью расстояние от  до ближайшего конца отрезка
до ближайшего конца отрезка  окажется больше
окажется больше  ?
? . Рассмотрим рисунок 2, на котором благоприятные исходы заштрихованы. Тогда искомая вероятность равна отношению длины заштрихованного отрезка к длине всего отрезка
. Рассмотрим рисунок 2, на котором благоприятные исходы заштрихованы. Тогда искомая вероятность равна отношению длины заштрихованного отрезка к длине всего отрезка  . То есть
. То есть  .
. Решение. Элементарным исходом в этом опыте логично считать пару
 , где
, где 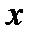 - время прихода первого человека, а
- время прихода первого человека, а 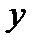 - время прихода второго. Будем считать, что
- время прихода второго. Будем считать, что 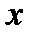 и
и  измеряются в минутах (после 14.00). Тогда
измеряются в минутах (после 14.00). Тогда  , а пара
, а пара 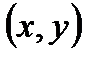 есть элемент декартова произведения
есть элемент декартова произведения 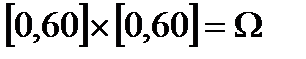 .
.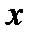 и
и  отличаются не больше, чем на 15 минут, то есть если
отличаются не больше, чем на 15 минут, то есть если 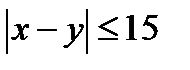 . На рисунке 3 эта область заштрихована.
. На рисунке 3 эта область заштрихована.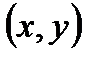 попадает внутрь заштрихованной области, то встреча состоится, а если вне области (на рисунке это точка (50,10)), то нет. Элементарный исход (50,10) означает, что второй приятель не дождется первого, поскольку пришел на 40 минут раньше. По условию все исходы
попадает внутрь заштрихованной области, то встреча состоится, а если вне области (на рисунке это точка (50,10)), то нет. Элементарный исход (50,10) означает, что второй приятель не дождется первого, поскольку пришел на 40 минут раньше. По условию все исходы  равновероятны, но поскольку их бесконечно много говорить о вероятности отдельного исхода не имеет смысла. Но можно говорить о вероятности попадания в какую-либо область, которая должна быть, очевидно, пропорциональна величине (мере) области. Мерой плоской области
равновероятны, но поскольку их бесконечно много говорить о вероятности отдельного исхода не имеет смысла. Но можно говорить о вероятности попадания в какую-либо область, которая должна быть, очевидно, пропорциональна величине (мере) области. Мерой плоской области  является площадь
является площадь 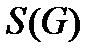 . В нашем случае
. В нашем случае 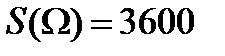 , а площадь заштрихованной части
, а площадь заштрихованной части  можно получить, вычитая площади двух прямоугольных треугольников (см. рисунок 3). Получаем
можно получить, вычитая площади двух прямоугольных треугольников (см. рисунок 3). Получаем  . Тогда доля благоприятных исходов равна
. Тогда доля благоприятных исходов равна  . Ее и естественно считать вероятностью встречи.
. Ее и естественно считать вероятностью встречи. и отстоящими друг от друга на расстояние
и отстоящими друг от друга на расстояние 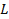 , наудачу бросается игла длины
, наудачу бросается игла длины 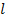 , (
, ( (см. рис.4). С какой вероятностью игла пересечет какую-либо линию?
(см. рис.4). С какой вероятностью игла пересечет какую-либо линию?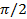


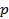

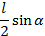


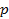 - расстояние от центра иглы до ближайшей прямой, а
- расстояние от центра иглы до ближайшей прямой, а 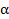 - угол между иглой и прямыми. Тогда
- угол между иглой и прямыми. Тогда 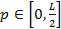 , а
, а 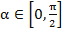 , причем считаем, что все эти значения равновозможны. Множеством элементарных исходов здесь будет прямоугольник, изображенный на рисунке 5. Выделим теперь благоприятные исходы.
, причем считаем, что все эти значения равновозможны. Множеством элементарных исходов здесь будет прямоугольник, изображенный на рисунке 5. Выделим теперь благоприятные исходы.
 (см. заштрихованное множество на рисунке 5). Тогда искомая вероятность равна отношению площадей, то есть
(см. заштрихованное множество на рисунке 5). Тогда искомая вероятность равна отношению площадей, то есть .
. . Результатом этого опыта (элементарным исходом) можно считать тройку чисел
. Результатом этого опыта (элементарным исходом) можно считать тройку чисел 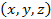 , то есть точку в кубе со стороной 1. Вероятность выбора точки из какой- либо части куба очевидно пропорциональна объему этой части. Поэтому применяем модель геометрических вероятностей. Рассмотрим события
, то есть точку в кубе со стороной 1. Вероятность выбора точки из какой- либо части куба очевидно пропорциональна объему этой части. Поэтому применяем модель геометрических вероятностей. Рассмотрим события  ,
,  и вычислим их вероятности.
и вычислим их вероятности.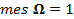 , то (см. рис. 6)
, то (см. рис. 6) 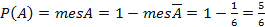
 Здесь
Здесь  находится и из геометрических соображений - это объем части куба над плоскостью
находится и из геометрических соображений - это объем части куба над плоскостью  (объем тетраэдра), который равен
(объем тетраэдра), который равен  .
. (см. рис. 7), она численно равна объему тетраэдра, ограниченного плоскостями:
(см. рис. 7), она численно равна объему тетраэдра, ограниченного плоскостями:  , следовательно,
, следовательно,  .
.