Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
Высшего профессионального образования
«Тюменский государственный университет»
Математический факультет
Кафедра алгебры и математического анализа
КУРСОВАЯ РАБОТА
на тему:
«Построение системы действительных чисел»
Студент: Камилов Эльмар Эмилевич
Группа: МиММ-160
Руководитель: доцент Девятков Антон Павлович
Оглавление
ВВЕДЕНИЕ……………………......................................................................................3
СИСТЕМА ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ................................................................3
ОПРЕДЕЛЕНИЕ………………………………………………………………………………………………12
АКСИОМЫПРОСТРАНСТВА ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ………………………………25
ЗАКЛЮЧЕНЕ…………………….................................................................................29
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ...................................................30
ПРИЛОЖЕНИЕ……….……………………………………..……………………………………………...31
Введение.
В данной статье я представлю метод построения системы действительных чисел через пару множеств, являющихся, так называемым, неполным сечением.
Основной раздел.
Глава 1.
Общее предложение из теории упорядоченных множеств.
Теорема. Пусть на множестве М задано бинарное отношение, которое
1) рефлексивно, т.е. x ≤ x для всех x ∈ M.
2) транзитивно, т.е. из x ≤ z и y ≤ z следует x ≤ z для всех x, y, z ∈ M.
3) x ≤ y или y ≤ x для любых y ∈ M.
Тогда отношение x ≈ y ≡ (x ≤ y и y ≤ x) является отношением эквивалентности. Определим на фактор-множестве M/≈ отношение, полагая x ≤ y, если x ≤ y для некоторых x ∈ X, y ∈ Y. Тогда ≤ является линейным порядком на M / ≈.
Глава 2.
Построение множества действительных чисел. Порядок.
Определение.
Множество R = { x, y, z,…} действительных чисел - множество мощности, на котором определены две операции (сложение и умножение) и отношение упорядоченности (x ≤ y), удовлетворяющие аксиомам:
I) 1. x + y = y + x;I.2.(x + y) + z = x + (y + z);
2. Существует такой элемент 0∈ R, что 0 + х = х для ∀ х ∈ R;
3. Для каждого элемента х ∈ R существует такой элемент - х, что х +
+ (- х)
II) 1. X · y = y · x;
2. (x · y) · z = x · (y · z);
3. Существует такой элемент 1∈ R, что 1· х = х для ∀ х ∈ R;
4. Для каждого элемента х ∈ R существует такой элемент х -1, что х · х -1 = 1;
III) 1. X · (y + z) = x · y + x · z;
IV) 1. Отношение {(x ≤ y) ∧ (y ≤ x)} эквивалентно отношению x = y;
2. Для любых двух элементов х ∈ R, y ∈ R или х ≤ у, или y ≤ x;
3. Из x ≤ y и y ≤ z следует x ≤ z;
4. Из x ≤ y следует x + z ≤ y + z для любых x, y, z ∈ R;
5. Из 0 ≤ x и 0 ≤ y следует 0 ≤ x · y;
Отношение x ≤ y записывается также в форме y ≥ x. Отношение {(x ≤ y) ∧ (x ≠ y)} записывается в форме х <у.
Отношение x ≤ y записывается также в форме y ≥ x. Отношение {(x ≤ y) ∧ (x ≠ y)} записывается в форме х < у.
V) Аксиома непрерывности: для любых элементов х ∈ R, y ∈ R таких, что х < у, существует элемент z ∈ R, такой что х < z < у.
VI) Аксиома Архимеда: для любых элементов х ∈ R, y ∈ R таких, что 0 < х, 0 < у, существует такое натуральное число n, что у ≤ n · х;
VII) Аксиома о вложенных отрезках: если {[ an, bn ]} - счётная последовательность отрезков, таких что an ≤ an +1 и bn +1 ≤ bn, при ∀ n, то пересечение этой последовательности непусто, т.е. ∃ х ∈ R: х ∈ [ an, bn ] для ∀ n.
Пусть Q - множество рациональных чисел. Пару множеств (A, A’), (A, A’) ⊂ Q назовём неполным сечением, если
1) A ≤ A’, т.е. a ≤ для всех a ∈ A, a’ ∈ A’;
2) для любого положительного r ∈ Q, найдутся числа a ∈ A, a’ ∈ A’ такие, что a’ – a < r.
Множество всех неполных сечений обозначим через M.
Введем на множестве M отношение ≤, полагая (A, A’) ≤ (B,B’) если A
Проверим выполнение условий теоремы из п.1.
1) (A, A’) ≤ (A,A’) верно, т.к. A ≤ A’;
2) Пусть (A, A’) ≤ (B, B’) и (B, B’) ≤ (C, C’) Предположим, что (A, A’) (C, C’) т.е. A ≤ A’. Тогда найдутся a ∈ A, и c ∈ C’ такие, что a > c’. Имеем, B ≤ c’ < a. Возьмём r ∈ Q+ такое, что c’ + r < a, например, r = (a – c’)/2. Для этого r найдутся b ∈ B и b’ ∈ B’ такие, что b’ – b < r. Но тогда из b ≤ c’ < a и b’ – b < r получаем b’ < b + r ≤ c’ + r < a. Неравенство b’ < a противоречит заданному условию A ≤ B. Значит, наше предположение неверно, и (A, A’) ≤ (C, C’).
3) Пусть (A, A’) < (B, B’), т.е. A < B’, Тогда найдутся a ∈ A, b’ ∈ B такие, что a > b’. Имеем, B ≤ b’ < a ≤ A’. Следовательно,(B, B’) ≤ (A, A’);
Условия теоремы выполнены. Фактор-множество 
называется множеством действительных чисел 
. Его элементы - классы эквивалентных неполных сечений будем обозначать греческими буквами α, β, γ, … Класс эквивалентности, содержащий неполное сечение (A, A’) будем обозначать [A, A’].
Для α, β ∈ R полагаем α < β, если α ≤ β и α ≠ β.
Глава 3.
Сложение.
Для A, B ⊂ Q полагаем A + B = {a + b|a ∈ A, b ∈ B}. Нетрудно проверить, что если (A, A’) и (B, B’) - неполные сечения, то (A + B, A’ + B’) и (-A’, -A) - неполные сечения. Проверки требует только условие 2 в определении неполного сечения. Если r ∈ Q, r > 0, и a’ – a < r/2, a ∈ A, a’ ∈ A’, b’ - b < r/2, b ∈ B, b’, то (a’ + b’) – (a + b) < r, a + b ∈ A + B, a’ + b’ ∈ A’ + B’.
Если α = [A, A’], β = [B, B’], то полагаем α + β = [A + B, A’ + B’], Надо проверить, что это определение корректно, т.е. результат сложения не зависит от выбора представителей из классов эквивалентности.
Пусть (A, A’) ~ (A₁, A₁’), (B, B’) ~ (B₁, B₁’) Надо проверить, что (A + B, A’ + B’) ~ (A₁+ B₁, A₁’ + B₁’). Так как A ≤ A’, B ≤ B₁’, то A + B ≤ A₁’ + B₁’. Аналогично, так как A₁ ≤ A’, B₁≤ B’, то A₁ + B₁ ≤ A’+ B’. Таким образом, (A + B, A’ + B’) ≤ (A₁ + B₁, A₁’ + B’) и (A₁ + B₁, A₁’ + B₁’). (A₁ + B₁, A₁’ + B₁’) ≤ (A + B, A’ + B’), т.е. (A + B, A’ + B’) ~ (A₁ + B₁, A₁’ + B₁’).
Свойства сложения.
Для любых α, β, γ ∈ R выполнено
1) (α + β) + γ = α + (β + γ);
2) α + β = β + α;
3) Существует элемент 0 ∈ R такой, что 0 + α = α для всех α ∈ R;
Это элемент 0 = |{0}, {0}|. Как обычно показывается, что элемент с таким свойством единственен.
4) Для любого α ∈ R существует элемент β ∈ R такой, что α + β = 0. Если α = [A, A’], то положим β = [-A’, -A]. Тогда α + β = [A – A’, A’ - A]. Так как A ≤ A’, то имеем A – A’ ≤ 0, 0 ≤ A’ – A, т.е. (A – A’, A’ - A) ~ ({0}, {0}). Значит, α + β = 0. Как обычно показывается, что элемент β с таким свойством единственен. Он обозначается β = -α.
7) Если α ≤ β, то α + γ ≤ β + γ.
Пусть α = [A, A’], β = [B, B’], γ = [C, C’], и α ≤ β, т.е. A ≤ B’. Надо проверить, что (A + C, A’ + C’) ≤ (B + C, B’ + C’), т.е. A + C ≤ B’ + C’. Это так, поскольку A ≤ B’ и С ≤ С’.
8) Если α < β, то α + γ < β + γ.
По предыдущему свойству α + γ ≤ β + γ. Если бы α + γ = β + γ, то прибавляя к обеим частям δ ∈ R такое, что γ + δ = 0, получили бы α = β, что неверно.
Глава 4.
Умножение.
Прежде всего полагаем 0 * α = 0 для всех α ∈ R.
Если α ≠ 0, то либо α > 0, либо α < 0. Рассмотрим, что означает каждый из этих случаев.
Пусть α = [A, A’] > 0. Так как 0 ≤ α, т.е. ({0}, {0}) ≤ (A, A’), то 0 ≤ A’, и так как 0 ≠ α, т.е. ({0}, {0}) /~ (A, A’), то A ≠ 0, т.е. существует α ∈ A такое, что α > 0. Отсюда A’ ≥ a > 0 Обратно, если существует a ∈ A такое, что a > 0, то [A, A’] > 0.
Аналогично, неравенство a = [A, A’] < 0 равносильно тому, что существует a’ ∈ A’ такое, что a’ < 0 и A ≤ a’ < 0. Понятно, что a = [A, A’] > 0 тогда и только тогда, когда – a = [-A’, -A] < 0. Через Q+ обозначим множество положительных рациональных чисел. Если a = [A, A’] > 0, то рассмотрим пару множеств A₁ = A ⋂ Q+, A₁’ = A’. Нетрудно проверить, что (A₁, A₁’)- неполное сечение и (A₁, A₁’) ~ (A, A’). Таким образом, для любого a > 0 найдется представитель (A₁, A₁’) ∈ a такой, что (A₁, A₁’) ⊂ Q+.
Пусть α > 0 и β > 0, α = [A, A’], β – [B, B’], A, A’, B, B’ ⊂ Q+. Проверим, что (AB, A’B’) - неполное сечение. AB ≤ A’B’ очевидно. Пусть r - произвольно малое рациональное положительное число. Подберем числа a ∈ A, a’ ∈ A’ такие, что a’- a < r и числа b ∈ B, b’ ∈ B’ такие, что b’ – b < r. При этом можно считать, что числа a’ и b не превосходят некоторых наперед фиксированных положительных рациональных чисел p и q. Тогда разность a’b’ – ab = a’(b’ - b) + b(a’ - a) < (p + q) r, т.е. может быть сделана сколь угодно малой, по теореме Фихтенгольца.
Полагаем αβ = [AB, A’B’], Точно также, как для сложения проверяется, что это определение не зависит от выбора представителей из классов эквивалентности.
Если α > 0, β < 0, то - β > 0, и полагаем αβ = - (α(-β)).
Если α < 0, β > 0, то – α > 0, и полагаем αβ = - α > 0, и полагаем
αβ = - ((-α)β);Если α < 0, β < 0, то – α > 0, - β > 0, полагаем αβ = (-α)(-β).
Свойства умножения.
⊂ ∈ ≤ ≥ > < ≠ αβγ δ ⋂
Для любых α, β, γ ∈ R выполнено:
1. (αβ) γ = α(βγ);
Если α, β, γ >, то утверждение тривиально следует из того, что (AB)C = A(BC) для A, B, C ⊂ Q+. Если одно из чисел равно нулю, то равенство справедливо. Если все числа отличны от нуля, то надо рассмотреть различные варианты знаков. Пусть, например, α < 0,
β > 0, γ < 0. Тогда
(αβ) γ = (-(-((-α)β)))(- γ) = ((-α)β)(- γ) = (-α)(β(-γ)) = (-α)(-(βγ)) = α(βγ);
2. αβ = βα;
Аналогично первому утверждению.
3. Существует элемент 1 ∈ R такой, что 1 * α = α. Для всех α ∈ R.
Это элемент 1 = [{1}, {1}]. Если α ≥ 0, то понятно. Если α < 0, то 1 * α = - (1 * α)) = - (-α). Единица единственна;
4. Для любого числа α ∈ R, α ≠ 0, существует число β ∈ R такое, что αβ = 1;
Пусть сначала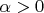 
, 
c 
. Нетрудно проверить, что 
является неполным сечением, причем 
. Проверим, что 
. Так как 
, то 
и 
, т.е. 
.
Если 
, то 
. Пусть 
, 
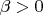. Тогда 
.
Число 
c указанным свойством единственно и обозначается 
.
5) 
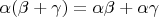
Докажем для положительных , 
, 
, где 
. Я не уверен, справедливо ли равенство 
, но даже если и неверно, то проверка все равно простая. Надо проверить, что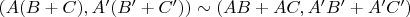 
. Так как, 
, 
, 
, то 
и 
. Следовательно, .
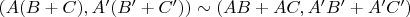Для отрицательных доказывается перенесением слагаемых из одной части равенства в другую.
6) Если 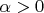, , 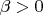то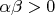 
Непосредственно следует из определения произведения и замечаний о критериях, когда .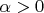
Пункт 5.
Аксиома непрерывности.
Пусть непустые множества 
таковы, что 
, т.е. 
для всех 
, 
. Тогда существует 
, что 
.
Доказательсвто. Пусть 
, 
. Положим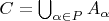 
. Так как 
для любых , , то 
. Пусть 
-- множество всех верхних граней для 
, т.е. множество таких 
, что 
. Так как , то 
. Нетрудно видеть, что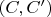 
-- неполное сечение (??? надо отдельно доказывать, что-то это не очевидно), и удовлетворяет неравенствам . Действительно, 
для всех и 
для всех 
.
Построение системы действительных чисел закончено.
Использованные источники
· Кудрявцев, Л. Д. Курс математического анализа. — 5-е изд. — М.: «Дрофа», 2003.
· Фихтенгольц, Г. М. Основы математического анализа. — 7-е изд. — М.: «ФИЗМАТЛИТ», 2002.
· Дедекинд, Р. Непрерывность и иррациональные числа = Stetigkeit und irrationale Zahlen. — 4-е исправленное издание. — Одесса: Mathesis, 1923.
· Зорич, В. А. Математический анализ. Часть I. — Изд. 4-е, испр.. — М.: «МЦНМО», 2002
· Ru.wikipedia.org
· Непрерывность функций и числовых областей: Б. Больцано, Л. О. Коши, Р. Дедекинд, Г. Кантор. — 3-е изд. — Новосибирск: АНТ, 2005.