Методические указания
И контрольные работы
По курсу высшей математики для студентов-заочников агрономического, зооинженерного факультетов.
Составитель: И.И. Аристова
Полесск 2011
Общие методические указания к выполнению контрольной работе.
Основной формой обучения студентов-заочников является самостоятельная работа над учебным материалом. Учебный материал следует изучать в той последовательности, которая приведена в методических указания. С программным материалом необходимо ознакомиться сначала по учебнику. После изучения теории надо перейти к разбору решенных в методических указаниях и учебнике задач. Затем можно переходить к решению задач из контрольного задания.
Контрольное задание должно быть выполнено в тетради, на обложке которой должны быть указаны фамилия и инициалы студента, его учебный шифр, факультет, номер группы, номер контрольной работы.
При выполнении контрольных работ следует учесть следующие рекомендации:
1. Необходимо указывать номер задачи и полностью записывать ее условие; решения задач надо располагать в порядке номеров, указанных в заданиях.
2. Решение всех задач сопровождать подробными пояснениями и вычислениями, ссылаясь на положения теории.
3. Чертежи и графики выполнять аккуратно, четко, с указанием единиц масштаба, координатных осей и других элементов чертежей.
4. Для удобства рецензирования на каждой странице следует оставлять широкие поля.
После получения прорецензированной работы студент обязан выполнить все указания рецензента и исправить ошибки. Вновь выполняются лишь неверно решенные задачи. Полностью переписывать работу не следует. Исправленная контрольная работа должна быть направлена на повторное рецензирование.
После получения зачтенной работы студент хранит ее у себя до экзамена. В период экзаменационной сессии студент обязан предоставить зачетные контрольные работы.
В тех случаях, когда студент при изучении теории или решении задач встретить затруднения, которые самостоятельно разрешить не удалось, он может обратиться за консультацией. Учебные консультации проводятся преподавателями кафедры высшей математики, как правило, во вторую и четвертую субботу каждого месяца, кроме июля и августа.
Для изучения курса рекомендуются следующие пособия:
1. Кудрявцев В.А., Демидович Б.П. «Краткий курс высшей математики» 1986.
2. Гмурман В.Е. «Теория вероятностей и математическая статистика» 1972.
Рекомендуются также следующие пособия, содержащие краткие теоретические сведения по программе и примерные решения задач:
3. Данко П.Е. и др. высшая математика в упражнениях и задачах. 1986.
4. Гмурман В.Е. руководство к решению задач по теории вероятностей и математической статистике. 1979.
Студент выполняет тот вариант контрольного задания, который совпадает с последней цифрой его учебного шифра. При этом, если предпоследняя цифра учебного шифра есть число нечетное (1,3,5,7,9), то номера задач для соответствующего варианта даны в таблице 1, если же предпоследняя цифра учебного шифра есть число или нуль (2,4,6,8,0), то номера задач для соответствующего варианта в таблице 2.
Табл. 1.
| вариант | Номера задач контрольного задания. | |||||||||||||
Табл. 2.
| вариант | Номера задач контрольного задания. | |||||||||||||
Указания к выполнению контрольной работы.
Тема 1. определители и системы линейных алгебраических уравнений.
Основные вопросы теории:
- Определители второго и третьего порядка. Их свойства.
- Решение систем трех линейных уравнений с тремя неизвестными по формулам Крамера.
Примеры решения задач.
Задача 1.
Вычислить определитель второго порядка 

Решение:
Определитель второго порядка вида Δ= 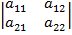
Выполняется по формуле Δ=  .
. 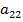 -
-  .
.  ,
,
поэтому  = 2 •4 - (- 1) • 3 = 8 – (- 3) = 11
= 2 •4 - (- 1) • 3 = 8 – (- 3) = 11
Ответ: 11.
Задача 2.
Вычислить определитель третьего порядка 
Решение:
Определитель третьего порядка вычисляется следующим разом:
 =
=  .
.  -
-  .
.  +
+  .
. 
Определители второго порядка являются минорами элементов первой строки. Они получается из исходного определителя вычеркиванием строки и столбца, содержащих соответствующий элемент.
Итак,  = 1·
= 1· 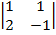 - (-2) ·
- (-2) · 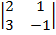 +(-3)·
+(-3)· 
Откуда, вычислив определители второго порядка, имеем
(- 1 – 2)+2·(- 2 – 3) - 3·(4 – 3) = - 16
Ответ: - 16.
Задача 3.
Решить систему трех линейных алгебраических уравнений с тремя неизвестными по формулам Крамера:

Решение.
Если главная системы отличен от нуля, то система совместна и имеет единственное решение, которое определяется по формулам Крамера: x=  , y=
, y=  ,z=
,z= 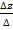 ,
,
где ∆ главный определитель системы, составленный из коэффициентов при неизвестных; ∆x, ∆y, ∆z–вспомогательные определители системы, которые получаются из главного определителя путем замены столбца коэффициентом при соответствующем неизвестном столбцом свободных членов.
Составим и вычислим определители системы:
∆=  =2·
=2· 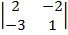 – (- 1)·
– (- 1)· 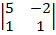 +3·
+3· 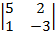 = - 52
= - 52
∆х=  = 4·
= 4· 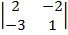 -(-1)·
-(-1)·  +3·
+3· 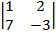 = - 52
= - 52
∆y= 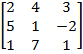 = 2·
= 2·  - 4
- 4  +3 ·
+3 ·  = 104
= 104
∆z=  = 2·
= 2· 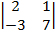 - (-1) ·
- (-1) ·  + 4 ·
+ 4 · 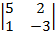 =0
=0
По формулам Крамера находим:
x = 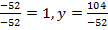 = -2, z =
= -2, z = 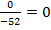 .
.
Выполним проверку, поставив найденные значения неизвестных в уравнениях системы:
2·1-(-2)+3·0=4,
5·1+2·(-2)-2·0=1,
1-3·(-2)+0=7.
Равенства выполняются, следовательно, система решена правильно.
Итак, для донной системы x=1, y=-2, z=0.
Тема 2. Элементы аналитической геометрии на плоскости.
Основные вопросы теории.
1. Прямоугольная система координат на плоскости.
Расстояние между двумя точками, деление отрезка в данном отношении. Текущие координаты.
2. Уравнение прямой с угловым коэффициентом. Общее уравнение прямой и его исследование. Уравнение прямой, проходящей через данную точку в данном направлении. Уравнение прямой, проходящей через две данные точки. Уравнение прямой в «отрезках». Пересечение двух прямых.
3. Угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых.
4. Кривые второго порядка: окружность, эллипс, гипербола, парабола.
Примеры решения задач.
Задача 4. Дан треугольник с вершинами А(-2;0), В(2;6) и С(7;1).
Найти:
1) Уравнение стороны ВС;
2) Уравнение высоты, проведенной из вершины А;
3) Длину этой высоты;
4) Уравнение медианы, проведенной из вершины С;
5) Уравнение средней линии треугольника, параллельной АС;
6) Уравнение окружности, для которой сторона АВ служит диаметром.
Решение.
1. Для составления уравнения прямой ВС пользуемся уравнением прямой, проходящей через две точки
 =
=  .
.
причем безразлично, координаты какой из двух данных точек принять за  и
и  , а какой за
, а какой за  и
и 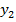 , лишь бы не изменять порядок индексов при xиy в правой и левой чпстях уравнения. Возьмем, например, так:
, лишь бы не изменять порядок индексов при xиy в правой и левой чпстях уравнения. Возьмем, например, так:  =
= 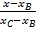 .
.
Подставив в это уравнение координаты точек  = 2,
= 2,  =6,
=6,  =7,
=7,  получим
получим

Откуда, умножив обе части уравнения на -5, имеем у-6=-х+2, или у=-х+8.
Итак, уравнение стороны ВС имеет вид: у=-х+8.
2. Уравнение прямой, проходящей через данную точку М0(х0,у0) в заданном направлении имеет вид:
у-у0= k ∙(х-х0).
Так как высота AD проходит через точкуА перпендикулярно стороне ВС, в качестве х0 и у0 возьмём координаты точки А(-2,0), а угловой коэффициент k найдём из условия перпендикулярности двух прямых: 
Так как k BC=-1, то k АD=1, и уравнение высоты AD примет вид: у=х+2.
3. Чтобы найти длину высоты AD, найдём координаты точки Dпересечения прямых BC и AD, решив систему уравнений:
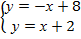
Сложив почленно обе части этих уравнений, имеем 2у=10, откуда y=5; вычитая их почленно, получаем 0=-2х+6, 2х=6, х=3.
Следовательно, D(3,5).
Теперь найдём длину AD как расстояние между точками A(-2,0) иD(3,5), подставив координаты точек A и D в формулу
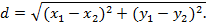
Получим: 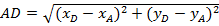 или
или

4. Чтобы написать уравнение медианы СЕ, надо найти координаты точки Е – середины стороны АВ. Находим их, применив формулы:
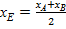 ,
, 
т.е. 
Уравнение медианы запишем, используя уравнение прямой, проходящей через две точки:

7y-21=-2xили 2x+7y-21=0 – уравнение медианы СЕ.
5. Уравнение средней линии EF будем искать в виде уравнения прямой через данную точку в заданном направлении (см. п.2).
Эта прямая проходит через точку Е параллельно прямой АС, поэтому в качестве х0 и у0 возьмём координаты точки Е, а угловой коэффициент найдём из условия параллельности прямых: k EF= k AC.
угловой коэффициент прямой АС  Так как А(-2,0) и С(7,1), то
Так как А(-2,0) и С(7,1), то 
Следовательно, 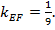
Итак, уравнение средней линии EF имеет вид: 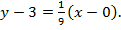
Следовательно, 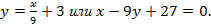
6. Уравнение окружности с диаметром АВ ищем в виде:
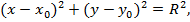
Где (x0;y0) –координаты центра окружности, т.е. точки E(0;3), а R = AE–радиус окружности.

Следовательно, уравнение окружности: x2 + (y – 3)2 = 13.
Построим треугольник АВС и все упомянутые линии в прямоугольной системе координатXOY:

ТЕМА 3. Введение в математический анализ.
Основные вопросы теории:
1. Переменная величина и область ее изменения. Понятие функции. Область определения функции.
2. Основные элементарные функции, их свойства и графики.
3. Предел переменной величины. Предел функции. Основные теоремы о пределах.
4. Бесконечно малая величина. Теоремы о бесконечно малых величинах. Бесконечно большая величина.
5. Сравнение бесконечно малых величин.
6. Первый замечательный предел: 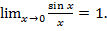
7. Второй замечательный предел:  число е; натуральный логарифм. Раскрытие простейших неопределителей.
число е; натуральный логарифм. Раскрытие простейших неопределителей.
8. Приращение аргумента и приращение функции.
9. Определение непрерывности функции в точке и на промежутке. Основные теоремы о непрерывных функциях. Точки разрыва функции.
Примеры решения задач.
Задача 5. Найти пределы указанных функций:
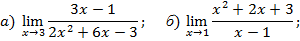
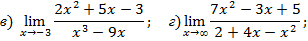

Решение:
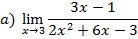
Данная дробно-рациональная функция при предельном значении аргумента х = 3 имеет знаменатель, отличный от нуля, и является непрерывной. Поэтому для нахождения ее предела при х → 3 достаточно аргумент х заменить его предельным значением, а именно:
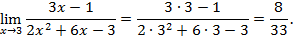
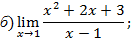
Числитель и знаменатель дроби – непрерывные функции и при х → 1 знаменатель есть величина бесконечно малая, а числитель имеет конечный предел, отличный от нуля. Итак, под знаком предела находится произведение функции х2 + 2х +3, имеющей конечный предел, отличный от нуля, на функцию  , которая при х →1 является бесконечно большой величиной как величина, обратная бесконечно малой величине. Поэтому данная функция является бесконечно большой. Условно это обозначается символом ∞.
, которая при х →1 является бесконечно большой величиной как величина, обратная бесконечно малой величине. Поэтому данная функция является бесконечно большой. Условно это обозначается символом ∞.
Следовательно, 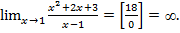

если непосредственно в данную функцию подставить вместо х его предельное значение
-3, то получим выражение вида  – неопределённость. В подобных случаях числитель и знаменатель необходимо разложить на множители, сократить дробь и затем перейти к пределу.
– неопределённость. В подобных случаях числитель и знаменатель необходимо разложить на множители, сократить дробь и затем перейти к пределу.
В числители находится квадратный трёхчлен вида ах2 + вх + с, корни которого находим по формуле:  а именно
а именно  , т.е.
, т.е. 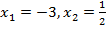
Так как 
то 
Знаменатель разложим на множители, вынося общий множитель х за скобки и применив формулу разности квадратов

Итак,  .
.

Теорему о пределе частного здесь применять нельзя, так как и числитель и знаменатель конечного предела не имеют. В этом случае говорят, что имеет место неопределённость вида  . В подобных примерах для раскрытия такой неопределённости можно разделить числитель и знаменатель на степень х с наивысшим показателем, а затем перейти к пределу. Деля числитель и знаменатель дроби на х2 и используя теоремы о пределах и свойства бесконечно малых величин получаем:
. В подобных примерах для раскрытия такой неопределённости можно разделить числитель и знаменатель на степень х с наивысшим показателем, а затем перейти к пределу. Деля числитель и знаменатель дроби на х2 и используя теоремы о пределах и свойства бесконечно малых величин получаем:


При х→∞ числитель и знаменатель дроби являются бесконечно большими величинами, т.е. имеем неопределённость  . Разделив числитель и знаменатель дроби на х3, перейдём к пределу при х →∞:
. Разделив числитель и знаменатель дроби на х3, перейдём к пределу при х →∞:
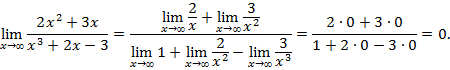
ТЕМА 4. Производная и дифференциал функции.
Основные вопросы теории:
1. Задачи, приводящие к понятию производной. Определение производной. Геометрический смысл производной.
2. Правила дифференцирования. Производная суммы и произведения нескольких функций. Дифференцирование сложной функции.
3. Формулы дифференцирования основных элементарных функций.
4. Понятие о дифференциале функции. Применение дифференциала для приближенного вычисления значений функции.
5. Производная второго порядка.
Для справки приводим основные правила дифференцирования:

| 
|

| 
|
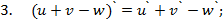
| 
|

| |
Если y=f(u), а u=u(x), то y=f(u(x)) – сложная функция от х. Производная сложной функции равна произведению этой функции по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменной x: 
Запишем теперь таблицу производных основных элементарных функций, давая рядом формулы для сложной функции.

| 
|
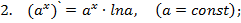
| 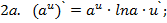
|

| 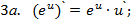
|

| 
|

| 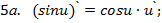
|

| 
|

| 
|

| 
|

| 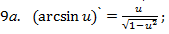
|

| 
|
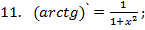
| 
|

| 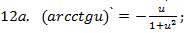
|
Примеры решения задач.
Задача 6.
Найти производные следующих функций:
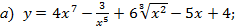
| 
|
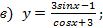
| 
|

Решение
А) Введем дробные и отрицательные показатели степени, вспомнив, что:

Получим 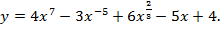
Применив правило дифференцирования аналитической суммы (3), правило вынесения постоянного множителя за знак производной (5), правило (1), а также формулу для производной степенной функции, получаем:
 откуда, используя формулы (*), (**), имеем:
откуда, используя формулы (*), (**), имеем:

б) По правилу дифференцирования произведения (4) и табличные формулы получаем:

в) Применяем правила дифференцирования дроби (6), суммы (3) и табличные формулы:


г) Применив (**), запишем функцию в виде степени  , а затем применим формулу производной сложной функции:
, а затем применим формулу производной сложной функции:
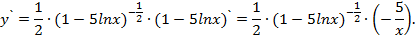
Ответ запишем, применив (*), (**): 
д) Применив формулу производной сложной функции и формулы таблицы производных, получаем:
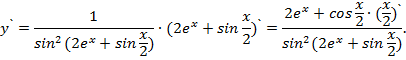
Так как 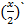 =
=  , то
, то 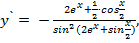 откуда умножив числитель и знаменатель на2, получаем ответ:
откуда умножив числитель и знаменатель на2, получаем ответ: 
Задача 7.
Найти дифференциал функции: 
Решение
Запишем функцию иначе: 
По определению, дифференциал dy функции y = f(x) вычисляется по формуле 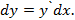
Поэтому сначала найдем производную данной функции, применив правила дифференцирования суммы (3) и произведения (4), формулу производной сложной функции и формулы таблицы производных:

Заметив, что 2sinx cosx = sin2x и вынося их из последних двух слагаемых за скобку  ,
,
Получаем: 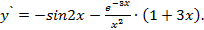
Найдем теперь дифференциал y:  .
.
ТЕМА 5. Применение производной к исследованию функций.
Основные вопросы теории.
1. Теоремы о возрастании и убывании функции.
2. Экстремум функции. Необходимое условие существование экстремума дифференцируемой функции. Достаточные условия существования экстремума.
3. Нахождение наибольшего и наименьшего значений непрерывной функции на заданном отрезке.
4. Выпуклость и вогнутость кривой. Точки перегиба графика функции. Дифференциальные признаки выпуклости, вогнутости кривой и точки перегиба
5. Общая схема исследования функций и построения их графиков.
Примеры решения задач.
Задача 8. Найти интервалы возрастания и убывания функции:
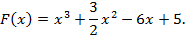
Решение:
Известно, что функция возрастает на тех интервалах, на которых ее первая производная положительна, и убывает там, где ее первая производная отрицательна. Границами интервалов возрастания и убывания функции являются точки экстремума. Из необходимого условия существования экстремума следует, что у дифференцируемой функции точки экстремума являются стационарными(критическими), т.е. в точках экстремума 
Найдем стационарные точки заданной функции 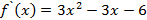 обращается в нуль.
обращается в нуль.
Когда 

На числовой оси отложим найденные значения 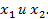 На полученных интервалах определим знак производной:
На полученных интервалах определим знак производной:
Таким образом, функция f(x) возрастает при 
и f(x) убывает при 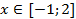
Задача 9.
Исследовать на экстремум функцию задачи 8.
Решение
Дифференцируемая функция имеет в критической точке экстремум, если  меняет знак при переходе через точку В данном случае при переходе через критические точки
меняет знак при переходе через точку В данном случае при переходе через критические точки 
Первая производная меняет знак, поэтому в этих точках есть экстемумы. При переходе через точку 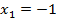 производная меняет знак с плюса на минус, следовательно, в этой точке функция имеет максимум:
производная меняет знак с плюса на минус, следовательно, в этой точке функция имеет максимум:

При переходе через точку  первая производная меняет знак с минуса на плюс, следовательно, в этой точке функция имеет минимум:
первая производная меняет знак с минуса на плюс, следовательно, в этой точке функция имеет минимум:

Задача 10.
Найти интервалы вогнутости и выпуклости перегиба графика функции 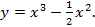
Решение:
Известно, что если вторая производная 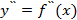 функции y = f(x) положительна (отрицательна) на некотором промежутке, то график такой функции на этом промежутке вогнутый (выпуклый). График функции имеет при
функции y = f(x) положительна (отрицательна) на некотором промежутке, то график такой функции на этом промежутке вогнутый (выпуклый). График функции имеет при  точку перегиба, если
точку перегиба, если 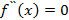 и вторая производная
и вторая производная  меняет свой знак при переходе через эту точку.
меняет свой знак при переходе через эту точку.
Найдем  и приравняем
и приравняем  к нулю: 6x-1=0 при
к нулю: 6x-1=0 при 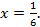
Исследуем знак  слева и справа от точки
слева и справа от точки 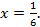
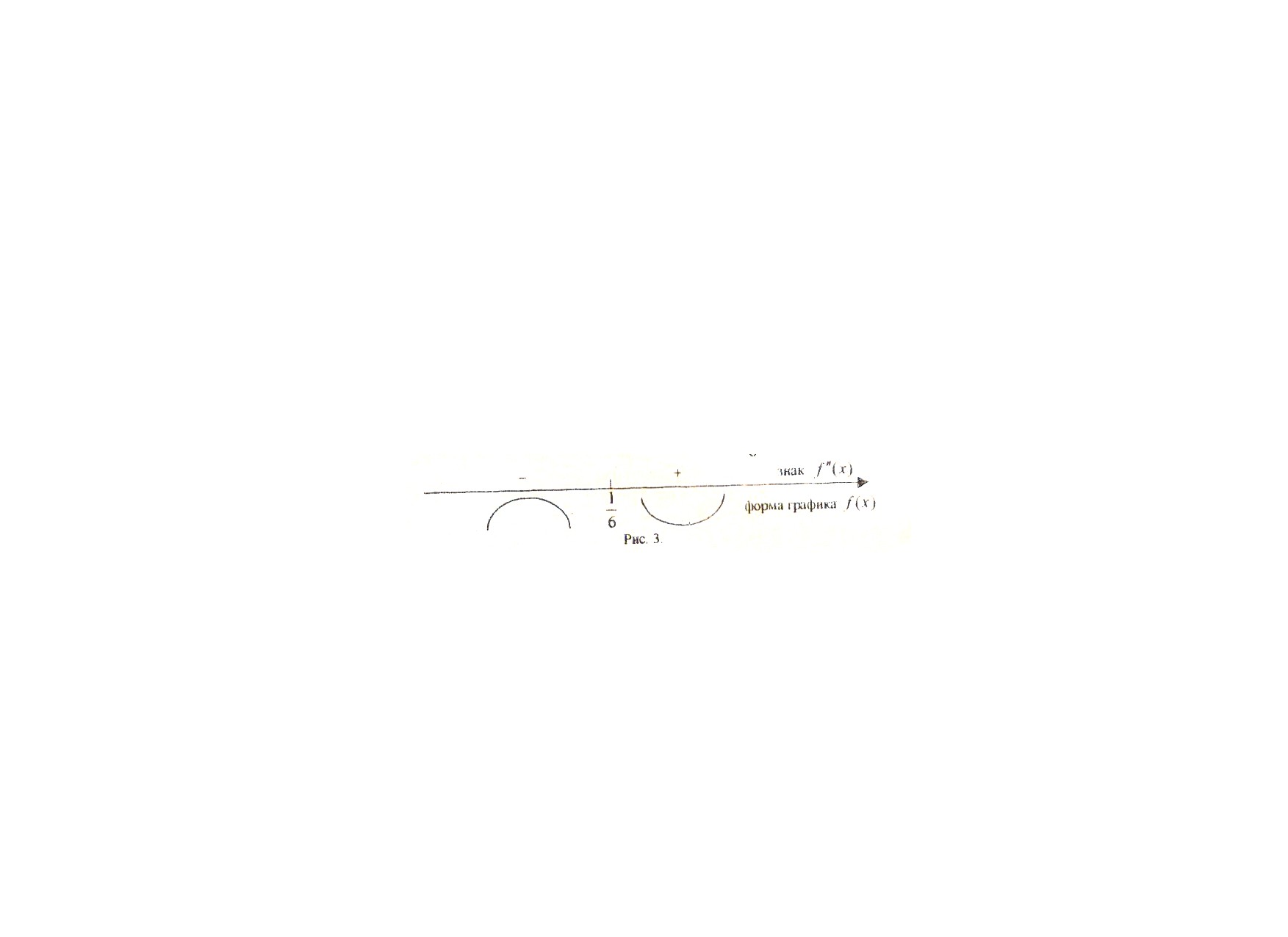
При 
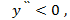 следовательно график функции выпуклый на интервале [
следовательно график функции выпуклый на интервале [ 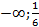 ]
]
При 
 , поэтому график функции вогнутый на интервале [
, поэтому график функции вогнутый на интервале [  ].
].
В точке 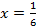 вторая производная обращается в нуль и меняет свой знак при переходе через нее, поэтому
вторая производная обращается в нуль и меняет свой знак при переходе через нее, поэтому 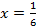 график имеет точку перегиба. Ордината точки перегиба
график имеет точку перегиба. Ордината точки перегиба
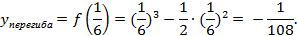
Итак, точка перегиба 
Задача 11.
Провести полное исследование функции 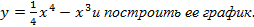
Решение.
1. Данная функция является многочленом, поэтому определена и непрерывна на всей действительной оси, т.е. при 
2. 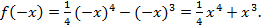
Так как не выполняются ни равенства f(-x) = f(x) (что явилось бы признаком четной функции), ни f(-x) = -f(x) (что свидетельствовало бы о нечетности функции), то данная функция общего вида.
3. При  , т.е. точки графика с возрастанием |х| удаляются наверх.
, т.е. точки графика с возрастанием |х| удаляются наверх.
4. Точки пересечения графика с осью ОХ найдем, приравняв y к нулю: 
или  , отсюда х = 0 или х = 4, т.е. график функции пересекает ось ОХ в точках О(0;0) и А(4;0)
, отсюда х = 0 или х = 4, т.е. график функции пересекает ось ОХ в точках О(0;0) и А(4;0)
Находя точки пересечения графика с осью OY и подставляя для этого в формулу функциональной зависимости значение х = 0, получаем ту же точку О(0;0).
5. Найдем промежутки возрастания и убывания (монотонного изменения) функции и точки экстремума.
Первая производная функции 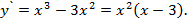
Критические точки найдем из условия 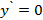 (необходимого условия экстремума дифференцируемой функции):
(необходимого условия экстремума дифференцируемой функции): 
Эти точки разделили действительную ось на три промежутка: [ 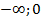 ], [
], [  ], [
], [  ].
].
Исследуя знак 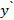 на каждом промежутке, убеждаемся, что при
на каждом промежутке, убеждаемся, что при 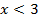 первая производная
первая производная  и, следовательно, функция убывает, а при
и, следовательно, функция убывает, а при  первая производная
первая производная  , т.е. функция возрастает.
, т.е. функция возрастает.

Результаты исследования схематически изображены на рис.4.
В критической точке x=3 – производная 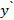 меняет свой знак с минуса на плюс, следовательно, x = 3 – точка минимума.
меняет свой знак с минуса на плюс, следовательно, x = 3 – точка минимума.

Итак, получена еще одна точка графика функции: B(3;-6.75).
6. Исследуем теперь формулу графика и найдем точки перегиба. Для этого найдем вторую производную функции 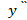 и, приравняв её к нулю, вычислим корни получившегося уравнения:
и, приравняв её к нулю, вычислим корни получившегося уравнения:

Точки х=0 и х=2 разбивают числовую ось на три промежутка[ 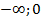 ],[0;2],[2;+
],[0;2],[2;+  ]
] 
Исследуя знак 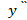 на каждом промежутке, видим, что:
на каждом промежутке, видим, что:
При 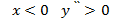 и график функции вогнутый;
и график функции вогнутый;
При  и график функции выпуклый;
и график функции выпуклый;
При  и график функции вогнутый;
и график функции вогнутый;
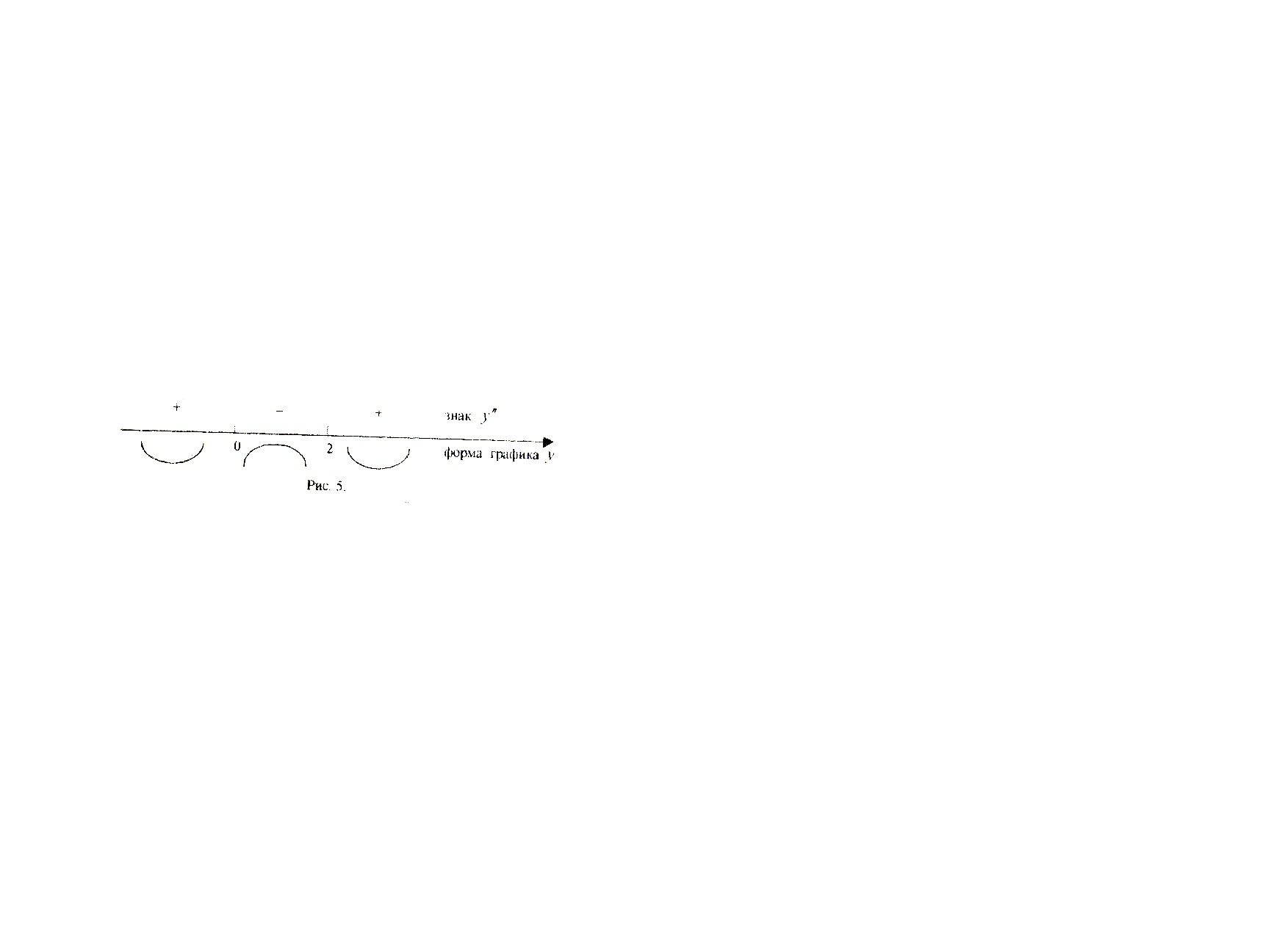
Схематически результаты исследования изображены на рис.5:
В точках х=0 и х=2 есть перегиб, так как в них вторая производная равна нулю (т.е. выполняется необходимое условие существования точки перегиба) и 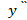 меняет знак при переходе через эти точки (выполнено и достаточное условие существования точки перегиба).
меняет знак при переходе через эти точки (выполнено и достаточное условие существования точки перегиба).
Вычислим ординаты точек перегиба:

Итак, О(0;0) и С(2;4) – точки перегиба.
7. На основании всех полученных данных строим график функции. Для этого отмечаем на плоскости XOY найденные точки О, А,В и С. Можно найти координаты дополнительных точек. Найдем например, 
Итак, Д(-1;1.25) – дополнительная точка графика.
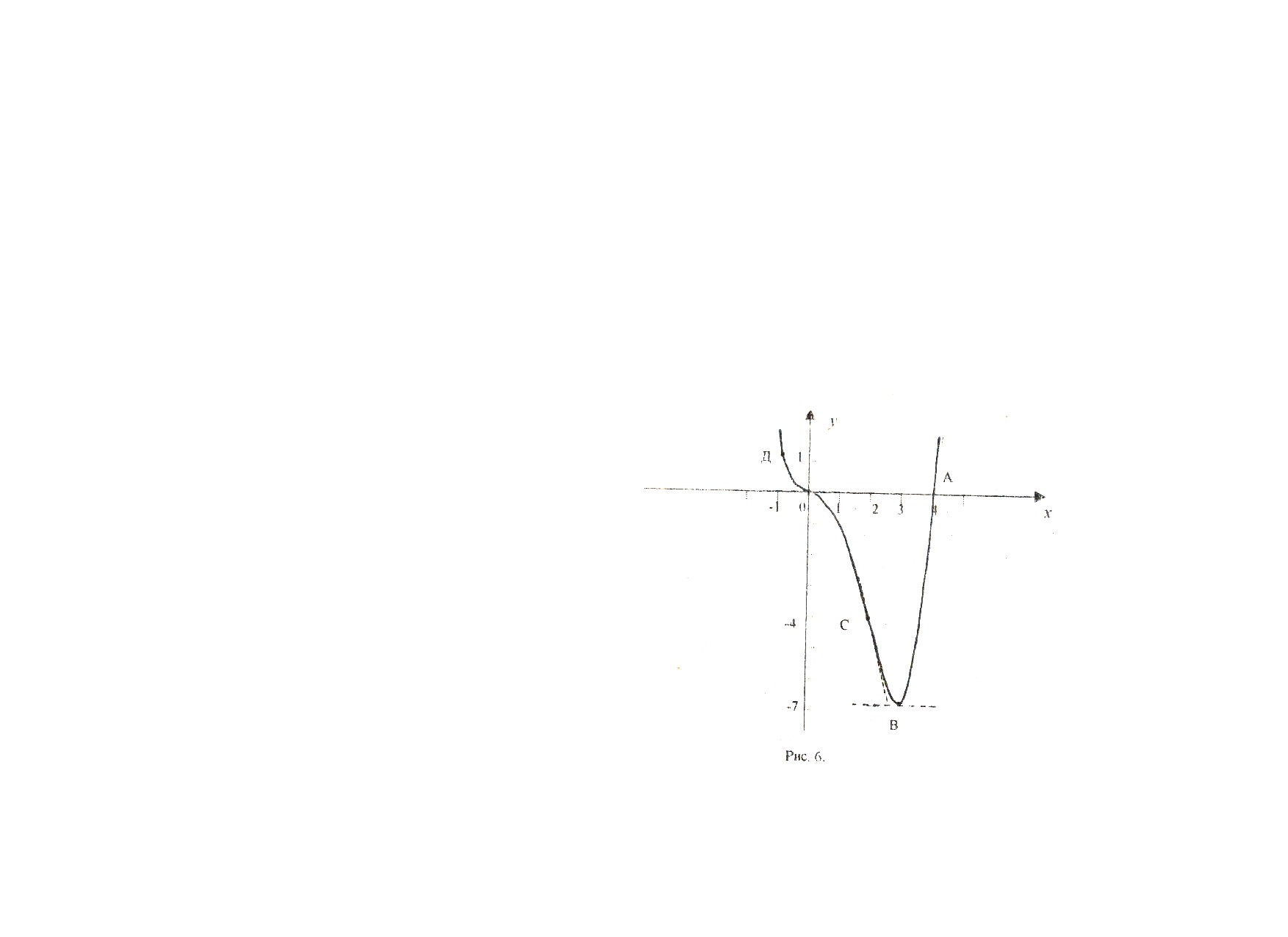
Замечание1. При построении графика функции нужно иметь ввиду, что на участках выпуклости график функции расположен под касательной, проведенной в любой точке, а на участках вогнутости, наоборот, - над касательной. В точках перегиба график переходит с одной стороны касательной на другую (см. рис.6, точки О и С).
В экстремальных точках касательная параллельна оси ОХ (см. рис6, точка В).
Замечание2. Для нахождения точек экстремума можно пользоваться и вторым достаточным условием: если в критической точке 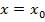 вторая производная дифференцируемой функции отлична от нуля, то в этой точке есть экстремум. Это максимум, если
вторая производная дифференцируемой функции отлична от нуля, то в этой точке есть экстремум. Это максимум, если  , и минимум, если
, и минимум, если  .
.
Например, в задаче 11, х=0, х=3 - критические точки.
Найдем в этих точках 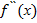 ;
;  , поэтому, требуется исследовать знак
, поэтому, требуется исследовать знак 
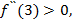 следовательно, в точке х=3 функция имеет минимум.
следовательно, в точке х=3 функция имеет минимум.
Задача 12. Найти наименьшее и наибольшее значение функции 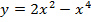 на отрезке [
на отрезке [ 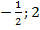 ]
]
Решение