Оглавление
Список сокращений.................................................................................................................... 3
Введение....................................................................................................................................... 4
1. Уравнения, не разрешенные относительно производной........................................ 5
1.1. Уравнения вида x=f(y,y’)................................................................................................ 5
1.2. Уравнения вида y=f(x,y’)................................................................................................ 6
1.3. Уравнение вида x=f(y’)................................................................................................... 7
1.4. Уравнение вида y=f(y’).................................................................................................. 7
2. Нормальная форма уравнения, не разрешенного относительно производной, в окрестности регулярной особой точки......................................................................................................... 8
2.1. Особые точки.................................................................................................................. 8
2.2. Криминанта..................................................................................................................... 9
2.3. Дискриминантная кривая.............................................................................................. 9
2.4. Точки касания криминанты с контактной плоскостью............................................ 10
2.5. Регулярные особые точки............................................................................................ 10
2.6. Теорема о нормальной форме...................................................................................... 10
2.7. Замечания и следствие из теоремы............................................................................. 13
3. Примеры решения типовых уравнений...................................................................... 15
3.1. Пример 1........................................................................................................................ 15
3.2. Пример 2........................................................................................................................ 16
3.3. Применение в «жизни»................................................................................................ 16
Заключение................................................................................................................................ 18
Литература................................................................................................................................. 19
Список сокращений
Русскоязычные сокращения
| ОДУ | Обыкновенные дифференциальные уравнения |
| Т.е. | То есть |
Введение
Дифференциальные уравнения являются одним из основных понятий современной математики. Дифференциальные уравнения, полученные в результате исследования какого-либо реального явления или процесса, называют дифференциальной моделью этого явления или процесса. Современное развитие физики и техники невозможно без использования дифференциальных уравнений. В данной курсовой работе рассматриваются обыкновенные дифференциальные уравнения, не разрешенные относительно производной, а также исследование теоремы о нормальной форме уравнения, не разрешенного относительно производной в окрестности регулярной особой точки.
Цель курсовой работы
Более общий анализ отдельного раздела ОДУ.
Методы исследования
В работе применен комплексный подход, заключающийся в использовании методов решения ОДУ и теории математического анализа.
Структура курсовой работы
Работа состоит из трех глав. В первой главе рассмотрены обыкновенные дифференциальные уравнения первого порядка, не разрешенные относительно производной.
В разделе 1.1 описаны основные термины и понятия, а также описывается основной метод решения таких уравнений. В последующих разделах (1.2 – 1.5) описываются несколько обобщенных случаев таких уравнений и метод их решения
Глава 2 посвящена теореме о нормальной форме уравнения, не разрешенного относительно производной в окрестности регулярной особой точки. В разделе 2.1 представлены вспомогательные, и в тоже время основные определения такого типа уравнений. В разделе 2.2 строится определение криминанты уравнения. В разделе 2.3. формулируется, непосредственно, сама теорема, ее пояснение и следствие из неё. В разделе 2.4 представлено подробное доказательство.
В заключительной третьей главе представлена практическая часть курсовой работы.
Уравнения, не разрешенные относительно производной
Уравнение вида
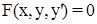(1),
где 
- непрерывная функция, называется уравнением первого порядка, не разрешенным относительно производной. Если это уравнение можно решить относительно 
, то мы получаем одно или несколько явных дифференциальных уравнений вида
.
Далее мы предполагаем, что дифференциальное уравнение не приводится к явной форме. Основной метод решения таких неявных уравнений − это метод введения параметра. Ниже мы покажем, как этот метод используется для нахождения общего решения для некоторых важных частных случаев уравнений, не разрешенных относительно производной.
Стоит отметить, что общее решение может не покрывать все возможные решения дифференциального уравнения. Помимо общего решения, дифференциальное уравнение может также содержать так называемые особые решения. Рассмотрим несколько типов таких уравнений.
1.1. Уравнения вида x=f(y,y’)
В этом случае переменная 
выражается явно через переменную 
и ее производную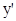 
. Введем параметр 
. Продифференцируем уравнение 
по переменной . Получаем следующее:
.
Поскольку 
, то последнее выражение можно записать в виде:
.
Получаем явное дифференциальное уравнение, общее решение которого описывается функцией
,
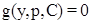где 
- произвольная постоянная.
Таким образом, общее решение исходного дифференциального уравнения определяется в параметрической форме системой двух алгебраических уравнений:
Если из этой системы исключить параметр 
, то общее решение можно выразить в явном виде 
.
1.2. Уравнения вида y=f(x,y’)
Здесь мы встречаемся с похожим случаем, но теперь переменная явно зависит от и 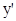. Введем параметр и продифференцируем уравнение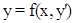 
по переменной . В результате имеем:
или 
.
Решая последнее дифференциальное уравнение, получаем алгебраическое уравнение 
. Вместе с исходным уравнением оно образует следующую систему уравнений:
,
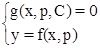которая описывает общее решение заданного дифференциального уравнения в параметрической форме. В некоторых случаях, когда параметр 
можно исключить из системы, общее решение записывается в явной форме 
.
1.3. Уравнение вида x=f(y’)
В данном случае дифференциальное уравнение не содержит переменную . Используя параметр , легко построить общее решение уравнения. Так как 
и
,
то справедливо соотношение:
.
Интегрируя последнее уравнение, получаем общее решение в параметрической форме:
.
1.4. Уравнение вида y=f(y’)
Уравнение такого типа не содержит переменную и решается аналогичным образом. Используя параметр , можно записать: 
. Отсюда следует, что
.
Интегрируя последнее выражение, получаем общее решение исходного дифференциального уравнения в параметрической форме:
.