I.1. Теоретическая карта №1

Рис. 1

 

Определение подобных треугольников

∆ А₁В₁С₁~ ∆АВС: и , где

k – коэффициентподобия треугольников.

 

Признаки подобия треугольников

2.1. (по двум углам).

2.2. (по двум сторонам и углу между ними).

2.3. (по трем сторонам).

 

Отношения величин в подобных треугольниках

Пусть коэффициент подобия ∆А₁В₁С₁ и ∆АВС равен k. Тогда

3.1. где - длины медиан∆А₁В₁С₁, а – длины медиан ∆АВС.

3.2. где – длины высот ∆А₁В₁С₁, а
длины высот ∆АВС.

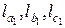3.3. где - длины биссектрис ∆А₁В₁С₁, а –
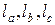длины биссектрис ∆АВС.

3.4. где 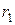- длинарадиуса окружности, вписанной в ∆А₁В₁С₁, а r – длина

радиуса окружности, вписанной в ∆АВС.

3.5. где R₁ – длина радиуса окружности, описанной около ∆А₁В₁С₁, а
R – длина радиуса окружности, описанной около ∆АВС.

3.6. где Р₁ – периметр ∆А₁В₁С₁, а Р – периметр ∆АВС.

3.7.

4. Способы получения подобных треугольников

4.1. А₁С₁׀׀АС: ∆А₁ВС₁~∆АВС. 4.2. ∆АВС – остроугольный,

АА₁ 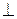ВС, СС₁ 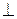АВ:
∆А₁ВС₁~∆АВС

с коэффициентом
подобия k =cosB.

I.2. Доказательства утверждений теоретической карты №1

Доказательства признаков подобия треугольников приводятся в учебнике [4, стр. 137 - 138], в учебнике [9, cтр. 176-180]. Докажем утверждения 3.1–3.7.

3.1.

 

Рис. 4

 

Дано: ∆А₁В₁С₁~∆АВС с коэффициентом подобия k.

Доказать: длины медиан ∆А₁В₁С₁и ∆АВС.

Доказательство

∆А₁В₁М₁~∆АВМ по второму признаку, так как из подобия треугольников ∆А₁В₁С₁ и ∆АВС следует, что и . Тогда , то есть

 

3.2.

 

 

Дано: ∆А₁В₁С₁~∆АВС с коэффициентом подобия k.

Доказать: где - длины высот ∆А₁В₁С₁ и ∆АВС.

Доказательство

∆А₁В₁H₁~∆АВН по первому признаку, так как из подобия треугольников ∆А₁В₁С₁ и ∆АВС следует, что , а Тогда

 

3.3.

 

Рис. 6

Дано: ∆А₁В₁С₁~∆АВС с коэффициентом подобия k.

Доказать: 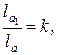где – длины биссектрис ∆А₁В₁С₁ и ∆АВС.

Доказательство

∆А₁В₁L₁~∆АВL по первому признаку, так как из подобия треугольников А₁В₁С₁ и АВС следует, что , а по определению биссектрисы, что Тогда

3.4.

 

 

Рис. 7

Дано: ∆А₁В₁С₁~∆АВС с коэффициентом подобия k.

Доказать: где r₁, r – длинырадиусов окружностей, вписанных в ∆А₁В₁С₁ и ∆АВС.

Доказательство

∆А₁О₁В₁~∆АОВ по первому признаку, так как из подобия треугольников А₁В₁С₁ и АВС следует, что , а А₁О₁, АО и В₁О₁,
ВО – биссектрисы углов А₁ и А, В₁ и В соответственно (центры О₁ и О окружностей, вписанных в ∆А₁В₁С₁ и ∆АВС, - точки пересечения биссектрис). Тогда согласно пункту 3.2

 

 

3.5.

 

 

Рис. 8

 

Дано: ∆А₁В₁С₁~∆АВС с коэффициентом подобия k.

Доказать: , где R₁, R длины радиусов окружностей, описанных около ∆А₁В₁С₁ и ∆АВС.

Доказательство

∆А₁О₁В₁~∆АОВ по первому признаку, так как из подобия ∆А₁В₁С₁ и ∆АВС следует, что Треугольники ∆А₁О₁В₁ и ∆АОВ – равнобедренные (А₁О₁=О₁В₁=R₁, АО=ОВ=R), следовательно, Тогда

3.6.

Дано: ∆А₁В₁С₁~∆АВС с коэффициентом подобия k.

Доказать: , где Р₁ и Р – периметры ∆А₁О₁В₁ и ∆АОВ.

Доказательство

∆А₁В₁С₁~∆АВС с коэффициентом подобия k, следовательно, А₁В₁=k∙АВ, В₁С₁=k∙ВС, А₁С₁=k∙АС. Р₁= А₁В₁+ В₁С₁+ А₁С₁= k∙АВ + k∙ВС + k∙АС=

=k∙(АВ+ВС+АС)=Р. Таким образом,

3.7. Доказательство данного равенства приводится в учебниках [4, стр. 134] и [9, стр.222].

 

Доказательство того, что в случае 4.1 получается треугольник, подобный данному, тривиально и мы его не приводим. Докажем подобие треугольников в случае 4.2.

Дано: ∆АВС – остроугольный,

АА₁ 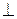ВС, СС₁ 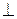АВ, А₁С₁ – прямая.

Доказать: ∆А₁ВС₁~∆АВС с коэффициентом
подобия k =cosB.

Доказательство

Треугольники АА₁В и СС₁В – прямоугольные, угол В у них общий, следовательно, они подобны по первому признаку. Тогда их стороны

пропорциональны, то есть . В треугольниках А₁ВС₁ и АВС угол В – общий, стороны пропорциональны, следовательно, они подобны по второму признаку. Их коэффициент пропорциональности равен . В прямоугольном треугольнике АА₁В отношение равно косинусу угла В. Таким образом, k = сosB.

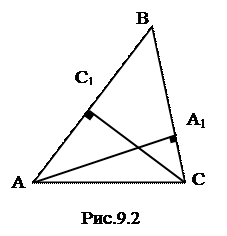Замечание. В процессе доказательства был рассмотрен ещё один способ получения подобных треугольников: проведение двух высот в остроугольном треугольнике. Они «отсекают» подобные треугольники.

 

DАВА₁~DСВС₁