ЗАДАЧИ НА СУББОТУ, КОТОРЫЕ МЫНЕ ПРОРЕШАЛИ
- Решить в целых числах уравнение (к – натуральное число, большее 1):
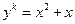 .
.
- Решить в натуральных числах уравнение:

3. Найдите все натуральные m и n, для которых выполняется равенство: m! +12 = n 2.
4. Какую наименьшую сумму цифр может иметь число вида 3n2+n+1 при натуральном n?
5. Решить в целых числах уравнение 2 n + 7 = x 2.
РЕШЕНИЯ (Конечно, не все возможные способы, а по одному. Вы можете придумать свой)))))
- Решить в целых числах уравнение (к – натуральное число, большее 1):
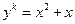 .
.
Решение
yk = x (x + 1). Если в разложение y на простые множители входит pn, то yk делится на pnk; значит (поскольку x и x + 1 взаимно просты), ровно одно из чисел x, x + 1 делится на pnk. Следовательно, | x | и | x + 1| являются k -ми степенями. При k ≠ 1 это возможно, лишь когда одно из чисел равно нулю, а второе – единице. В любом случае y = 0.
Ответ
(0, 0) и (–1, 0).
2. Решить в натуральных числах уравнение: 
Решение
Второе слагаемое положительно, но меньше единицы. Поскольку 10/7 = 1 + 3/7, то x = 1, а y + 1/ z = 7/3 = 2 + 1/3.
По тем же соображениям y = 2, z = 3.
Ответ x = 1, y = 2, z = 3.
3. Найдите все натуральные m и n, для которых выполняется равенство:
m! +12 = n 2.
Решение
При  значение m! кратно 2 и кратно 5, то есть, десятичная запись этого числа оканчивается нулем, поэтому, число m! + 12 оканчивается цифрой 2, следовательно, оно не может быть квадратом натурального числа. Последовательно проверив значения m = 1; 2; 3; 4, получим, что m = 4; n = 6.
значение m! кратно 2 и кратно 5, то есть, десятичная запись этого числа оканчивается нулем, поэтому, число m! + 12 оканчивается цифрой 2, следовательно, оно не может быть квадратом натурального числа. Последовательно проверив значения m = 1; 2; 3; 4, получим, что m = 4; n = 6.
Ответ m = 4; n = 6.
4. Какую наименьшую сумму цифр может иметь число вида 3n2+n+1 при натуральном n?
Подсказка
Ответ: 3.
Решение
При n=8 сумма цифр числа 3n2+n+1 равна 3. Убедимся, что меньше сумма цифр не бывает. Действительно, число 3n2+n+1 всегда нечетно и больше 1, поэтому сумма его цифр не может быть равна 1. Если она равна 2, то это число должно иметь вид 10k+1, тогда 3n2+n=(3n+1)n=10k. Числа (3n+1) и n взаимно просты, следовательно либо меньшее из них (n) равно 1, а большее (3n+1) - 10k, либо n=2k, а 3n+1=5k. Первый случай, как легко проверить, невозможен. Во втором случае значения k=0,1 легко проверить непосредственно, а при k не меньше 2 получаем, что 5k/2k>52/22>4>(3n+1)/n.
Ответ 3
5. Решить в целых числах уравнение 2 n + 7 = x 2.
Решение
(x – 3)(x + 3) = x 2 – 9 = 2 n – 2 = 2·(2 n –1 – 1).
n = 0 не подходит, а при n > 0 правая часть четна, значит, оба множителя в левой части четны. Но тогда и 2 n –1 – 1 четно, то есть равно 0. Отсюда n = 1, x = 3.
Ответ n = 1, x = 3.
Следующая девятка задач: 1) не обращайте внимания на слова о поле ответа)
2) в субботу 2.02 Вейцмановская олимпиада, так что это на две недели…
Увы. Можем пообсуждать идеи и раньше.
1. 
Сережа может успеть за день либо собрать 5 компьютеров, либо настроить 8 компьютеров. Какое наибольшее количество компьютеров он может собрать и настроить за один день?
Числа 1/3, 1/5, 1/7 являются членами арифметической прогрессии. Найдите наибольшую возможную разность этой прогрессии.
4. Наибольший общий делитель натуральных чисел m и n равен 1. Каково наибольшее возможное значение наибольшего общего делителя чисел 30m+n и 50n+m?
4.
5. 
6. 
7. 
8. По горизонтальному желобу в одном направлении на одинаковом расстоянии друг от друга катятся шесть одинаковых шариков. Навстречу им катятся еще семь таких же шариков на том же расстоянии друг от друга. Скорости всех шариков одинаковы. При столкновении двух шариков они разлетаются в противоположные стороны с той же скоростью. Сколько всего столкновений произойдет между этими шариками?
9. Мама может съесть весь борщ за 19 минут, весь плов за 12 минут и торт за 30 минут. Вовочке на это требуется соответственно 6, 7 и 10 минут соответственно. Вовочка распределил продукты между собой и мамой таким образом, чтобы обед прошел как можно быстрее. Найдите сколько минут, потратили на обед мама с Вовочкой.