Понятие случайной величины сочетает в себе следующие понятия: опыт, случайное событие и переменная величина [1].
Опыт (эксперимент, испытание) – это воспроизведение некоторого комплекса условий. Опыт может быть повторен сколь угодно много раз.
Случайным событием, связанным с проведением некоторого опыта, называется всякий его исход, который появляться или нет в проведении данного опыта.
Если имеется случайное событие А, связанное в проведением опыта, то мерой появления события А в опыте служит вероятность его появления. Если опыт повторен n раз и в итоге событие А появилось m раз, то вероятностью p(A) события А называется относительная частота его появления в n бесконечно длинном ряду опытов.
Классическое определение вероятности события А: - это отношение числа случаев m, благоприятствующих ему, к общему числу случаев n, т.е. Р(A) = m/n. При определенных условиях в качестве оценки вероятности события Р(A) может быть использована статистическая вероятность Р*(A), т.е. относительная частота W(A) появления события А в n произведенных испытаниях.[2]
Одним из важнейших понятий теории вероятностей является понятие случайной величины. Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно — заранее не известно).
Более строго случайная величина X определяется как функция, заданная на множестве элементарных исходов (или в пространстве элементарных событий), т.е
X = f (ω),
где ω – элементарное событие, принадлежащее пространству Ω, т.е. ω є Ω.
Различают дискретные и непрерывные случайные величины.
Для дискретной случайной величины множество возможных значений случайной величины, т.е. функции f (ω) конечно или счетно, для непрерывной — бесконечно и несчетно.
Наиболее полным, исчерпывающим описанием случайной величины является ее закон распределения.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значения ми случайной величины и соответствующими им вероятностями.
Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически.
Такая таблица называется рядом распределения дискретной случайной величины. Для любой дискретной случайной величины закон распределения может быть задан:
- в виде таблицы
| X: | x 1 | x 2 | … | xi | … | xn |
| p 1 | p 2 | … | pi | … | pn |
- аналитически (в виде формулы), например, ниже приведен показательный (экспоненциальный) закон распределения с параметром λ, представленный через формулу плотности вероятности
- графически
При этом для дискретной случайной величины выполняется следующее соотношение:
Если по оси абсцисс откладывать значения случайной величины, а по оси ординат — соответствующие их вероятности, то получаемая (соединением точек) ломаная называется многоугольником распределения вероятностей.
Две случайные величины называются независимыми, если закон распределения одной из них не меняется от того, какие возможные значения приняла другая величина.
Закон распределения дискретной случайной величины дает исчерпывающую информацию о ней, так как позволяет вычислить вероятности любых событий, связанных со случайной величиной. Однако такой закон распределения бывает трудно обозримым, не всегда удобным (и даже необходимым) для анализа. Поэтому для описания случайных величин часто используются их числовые характеристики — числа [3], в сжатой форме выражающие наиболее существенные черты распределения случайной величины. Наиболее важными из них являются: математическое ожидание, дисперсия, среднее квадратическое отклонение и др.
Математическим ожиданием, или средним значением, М(Х) дискретной случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности:
(1.1)
Для математического ожидания также используются следующие обозначения: E (X),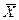 
.
Для выборки n дискретных случайных величин можно применять следующую формулу расчета математического ожидания:
(1.2)
Математическое ожидание обладает следующими свойствами:
1. E(С) = С, где С — постоянная величина;
2. E (кХ) = к E(Х);
3. E(Х ± Y) = E(Х) ± E(Y); (1.3)
4. E(X۰Y) = E(Х) • E(Y), где X, Y — независимые случайные величины;
5. E(Х ± C) = E(Х) ± С;
6. E(X - а) = 0, где а = E(Х).
Дисперсией D(Х) случайной величины X называется математическое ожидание квадрата ее отклонения от математического ожидания (обозначается также Var(X), σ2):
D(Х) = E[Х - E(Х)]2, (1.4)
или
D(Х) = E(Х – a) 2, где a = E(Х)
Дисперсия характеризует отклонение (разброс, рассеяние, вариацию) значений случайной величины относительно среднего значения (математического ожидания). Если случайная величина X — дискретная с конечным числом значений, то
(1.5)
Дисперсия D(X) имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому в качестве показателя рассеяния используют величину, называемую средним квадратическим отклонением (стандартным отклонением или стандартом), которая определяется значением корня квадратного из ее дисперсии, т.е.:
(1.6)
Дисперсия обладает следующими свойствами:
1. D(c) = 0, где c — постоянная величина;
2. D(kX) = k2D(X); (1.7)
3. D(X) = М(Х2) - а2, где a = M(X);
4. D(X ± Y) = D ( X) + D(Y), где X и Y — независимые случайные величины.
5. D(c1X +c2Y) = c21D ( X) + c22D(Y) +2c1c2CXY, где X и Y — случайные величины, а с1 и с2 – произвольные константы.
Упорядоченный набор Х = (Х1, Х2,..., Хn) случайных величин называется многомерной (n -мерной) случайной величиной (или системой случайных величин, n - мерным вектором). Например, характеристика автомобиля может быть охарактеризована многомерной случайной величиной Х = (Х1, Х2,..., Хn), где Х1 — мощность двигателя, Х2 — потребление бензина на 100 км, Х3 — время разгона до 100 км., Х4 — объем багажника, л., Х5 — максимальный тормозной путь при скорости 60 км/час и т.п.
Зависимость между двумя случайными величинами называется вероятностной (стохастической или статистической), если каждому значению одной из них соответствует определенное (условное) распределение другой. Например, зависимость длины пути торможения автомобиля от состояния дороги – вероятностная.
Ковариацией (или корреляционным моментом) Cov(X,Y) (другое обозначение Cxy) случайных величин X и Y называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий, т.е. Cxy = Cov(X,Y) = М[(Х- ах)۰(Y - ау)], где ах = М(Х), ау = M(Y). Ковариация двух случайных величин характеризует как степень зависимости случайных величин, так и их рассеяние вокруг точки (ах, ау).
Оценкой ковариации служит величина, называемая выборочной ковариацией, рассчитываемой по формуле:
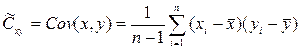(1.8)
Данная оценка обладает свойством несмещенности.
Замечание. В табличном процессоре Excel имеется функция расчета ковариации КОВАР, которая вычисляет ее по формуле:
Связь между оценкой 
и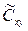 
задается соотношением
(1.9)
Ковариация — величина размерная, что затрудняет ее использование для оценки степени зависимости случайных величин. Поэтому чаще используется коэффициент корреляции.
Коэффициентом корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратических отклонений этих величин:
(1.10)
где 
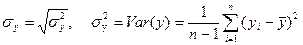
Коэффициент корреляции — величина безразмерная — характеризует тесноту линейной зависимости между случайными величинами.