
определяется как функция, обратная показательной функции, т.е. из уравнения

 ,
, 
Отсюда следует определение логарифмической функции:

| (1.16) |
Если положить k = 0 и наложить ограничение на 
 , то получим однозначную ветвь логарифмической функции, которую называют главным значением логарифмической функции и обозначают
, то получим однозначную ветвь логарифмической функции, которую называют главным значением логарифмической функции и обозначают

| (1.17) |
Пример 1.19
 ,
,
 ,
,  .
.
Отсюда следует, что
 . Главное значение
. Главное значение 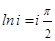 .
.
Пример 1.20
Найти  .
.
Решение
 = =
= =  =
=  ;
;
Окончательно, 
Если положить k = 0, то получим главное значение логарифма
 .
.
Производная функции комплексной переменной
И понятие аналитичности
Производной функции  в точке
в точке  называется предел отношения приращения функции
называется предел отношения приращения функции  к приращению аргумента
к приращению аргумента  при стремлении
при стремлении  к нулю:
к нулю:

| (1.18) |
Если этот предел существует при  по произвольному пути, то функция называется дифференцируемой в точке z. Если функция
по произвольному пути, то функция называется дифференцируемой в точке z. Если функция  дифференцируема во всех точках области
дифференцируема во всех точках области  , то она называется аналитической в этой области.
, то она называется аналитической в этой области.
Теорема: если функция  имеет непрерывные частные производные, то для аналитичности функции в этой области необходимо и достаточно выполнение условий
имеет непрерывные частные производные, то для аналитичности функции в этой области необходимо и достаточно выполнение условий
 ; ; 
| (1.19) |
Докажем необходимость этих условий. Рассмотрим предел

По условию функция  является аналитической, поэтому этот предел не зависит от пути, по которому
является аналитической, поэтому этот предел не зависит от пути, по которому  .
.
Пусть сначала  , а затем
, а затем  , тогда
, тогда

| (1.20) |
Пусть теперь сначала  , а затем
, а затем  , тогда
, тогда

| (1.21) |
В силу аналитичности функции  выражения (1.20) и (1.21) равны. Приравнивая их действительные части, получим первое равенство (1.19), а равенство мнимых частей приводит ко второму соотношению (1.19). Достаточность условий (1.19) примем без доказательства.
выражения (1.20) и (1.21) равны. Приравнивая их действительные части, получим первое равенство (1.19), а равенство мнимых частей приводит ко второму соотношению (1.19). Достаточность условий (1.19) примем без доказательства.
Соотношения (1.19) называются условиями Коши - Римана (иногда их так же называют условиями Даламбера - Эйлера).
Проверим выполнение условий (1.19) для функции  .
.
 ,
,  ;
;
 ,
,  ;
;
 ,
,  .
.
Оба условия (1.13) выполняются, поэтому показательная функция является аналитической. Аналогично можно доказать аналитичность всех остальных основных элементарных функций. То же относится ко всем вообще элементарным функциям, т.е. к функциям, которые составляются из основных элементарных с помощью конечного числа арифметических операций и операции взятия функции от функции.
Пример 1.21.
1)  - элементарная функция, следовательно она является аналитической всюду, кроме точки
- элементарная функция, следовательно она является аналитической всюду, кроме точки  , в которой эта функция не определена.
, в которой эта функция не определена.
2)  - функция не аналитическая:
- функция не аналитическая:  ,
, 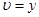 , условия (1.19) не выполняются.
, условия (1.19) не выполняются.
Дифференцирование функций комплексного переменного
При выводе условий (1.19) были получены две формулы вычисления производной

| (1.22) |

| (1.23) |
Рассмотрим функцию
 .
.
Найдем ее производную по формуле (1.22):  .
.
 ,
,  ,
,  .
.
Аналогично можно показать, что справедливы все формулы и правила дифференцирования, известные из теории функций действительного переменного:
 ,
,  ,,,,.
,,,,.
Интегрирование функций
Комплексной переменной
Пусть L некоторый контур в комплексной плоскости,  функция комплексной переменной z, а функции двух действительных переменных
функция комплексной переменной z, а функции двух действительных переменных  и
и  являются соответственно действительной и мнимой частью функции
являются соответственно действительной и мнимой частью функции  , то
, то
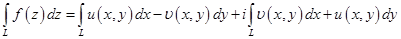
| (1.24) |
где  ,
,  ,
, 
 .
.
Это формула для вычисления интеграла по контуру.
Оба интеграла являются криволинейными интегралами второго рода в действительной плоскости.
Итак, вычисление интегралов по контуру сводится к вычислению двух криволинейных интегралов в действительной плоскости.
Пример 1.22
Вычислить интеграл  , L - отрезок прямой между точками
, L - отрезок прямой между точками  и
и  +1.
+1.
Решение


