Метод применяется в задачах поиска условного экстремума с ограничениями типа равенство и неравенств. Мы ограничимся рассмотрением поиска экстремума с ограничениями типа равенства.
Требуется решить задачу
 (4.4.1)
(4.4.1)
где функции f (X), ji (X) - выпуклые дифференцируемые функции.
Поиск решения состоит в построении последовательности точек { Xk }, вычисляемых по правилу
Xk +1= Xk + dXk (k =0, 1, …), (4.4.2)
где dXk - вектор, вычисляемый для каждого значения k из условия проекции вектора -Ñ f (Xk), k =0, 1, …, на аппроксимирующую плоскость, задаваемую уравнением
AkdXk = Tk, (4.4.3)
которая аппроксимирует в точке Xk (k =0, 1, …) поверхность П, задаваемую уравнениями ji (X)=0 (i =1, …, m). Здесь Ak - матрица
A (X)=  ,
,
вычисленная в точке X = Xk, Tk =-(j 1(Xk), …, jm (Xk))T.
Вектор dXk определяется по формуле
dXk = d 1 Xk + d 2 Xk (4.4.4)
где
d 1 Xk =- hk [ E -  (Ak
(Ak  )
)  Ak ]Ñ f (Xk)=- hk D Xk (4.4.5)
Ak ]Ñ f (Xk)=- hk D Xk (4.4.5)
- градиентная составляющая приращения, d 2 Xk =  (Ak
(Ak  )
)  Tk - компенсационная составляющая приращения.
Tk - компенсационная составляющая приращения.
Величина hk шага может выбираться как из условия убывания функции f (X) при переходе из точки Xk в точку Xk - hk [ E -  (Ak
(Ak  )
)  Ak ]Ñ f (Xk), так и из условия
Ak ]Ñ f (Xk), так и из условия
y (hk)= f (Xk - hk [ E -  (Ak
(Ak  )
)  Ak ]Ñ f (Xk))®
Ak ]Ñ f (Xk))® 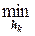 (4.4.6)
(4.4.6)
Задача (4.4.6) может решаться либо с использованием необходимых и достаточных условий минимума, либо с использованием численных методов.
Расчёт заканчивается в точке Xk, в которой |D Xk |£ e, | d 2 Xk |£ e, где e - заданное число. В полученной точке обязательна проверка выполнения достаточных условий минимума функции в исходной задаче (4.4.1). Если будет выполнено точное равенство d 1 Xk =- hk [ E -  (Ak
(Ak  )
)  Ak ]Ñ f (Xk)=
Ak ]Ñ f (Xk)= 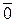 , то это означает, что выполнены точные необходимые условия экстремума. При этом вектор Lk множителей Лагранжа определяется по формуле
, то это означает, что выполнены точные необходимые условия экстремума. При этом вектор Lk множителей Лагранжа определяется по формуле
Lk =-(Ak  )
)  Ak Ñ f (Xk) (4.4.7)
Ak Ñ f (Xk) (4.4.7)
Если в задаче (4.4.1) ограничения линейны, то матрица A постоянна. При этом начальная точка X 0 попадает в ОДР за одну итерацию. В дальнейшем требуется вычисление только d 1 Xk.
Таким образом, алгоритм решения задачи - следующий:
1. Задать X 0, e ³0, k 0 - число итераций.
2. Найти A (X), Ñ f (X), D X =-[ E -  (A
(A  )
)  A ]Ñ f (X), d 2 X = A T(AA T)
A ]Ñ f (X), d 2 X = A T(AA T)  T (X) где T (X)=-(j 1(Xk), …, jm (Xk))T.
T (X) где T (X)=-(j 1(Xk), …, jm (Xk))T.
3. Положить k =0.
4. Проверить выполнение условия k ³ k 0:
а) если неравенство выполнено, то расчёт окончен. Вычислить Lk =-(Ak  )
)  Ak Ñ f (Xk), проверить необходимое условие минимума, оценить результаты;
Ak Ñ f (Xk), проверить необходимое условие минимума, оценить результаты;
б) если неравенство не выполнено, то перейти к шагу 5.
5. Вычислить матрицу Ak = A (Xk).
6. Вычислить d 2 Xk.
7. Вычислить | d 2 Xk |.
8. Вычислить D Xk.
9. Вычислить |D Xk |.
10. Проверить выполнение условий |D Xk |£ e и | d 2 Xk |£ e:
а) если условия выполняются, то расчёт окончен. Вычислить Lk и проверить достаточные условия минимума;
б) если |D Xk |> e, | d 2 Xk |£ e, то положить d 2 Xk =0 и перейти к шагу 11;
в) если |D Xk |£ e и | d 2 Xk |> e, то положить D Xk =0 и перейти к шагу 13;
г) если |D Xk |> e, | d 2 Xk |> e, то перейти к шагу 11.
11. Получить выражение для точки Xk +  D Xk.
D Xk.
12. Определить  из условия f (Xk + hk D Xk)®
из условия f (Xk + hk D Xk)® 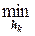 .
.
13. Вычислить Xk +1= Xk +  D Xk + d 2 Xk. Положить k = k +1 и перейти к шагу 4.
D Xk + d 2 Xk. Положить k = k +1 и перейти к шагу 4.
Если ограничения в задаче линейны, то при k ³1 на шаге 4 переходим к шагу 8. При этом на шаге 10 полагаем | d 2 Xk |=0.
Пример II. Найти условный экстремум функции:
f (X)=  ® min
® min
3 x 1-2 x 2-5=0.
Решение. 1. Задаём X 0=(1, -1) e =0,1, k 0=10 - число итераций.
2. Найдём A (X)=  =(3; -2), Ñ f (X)=(4 x 1, 8 x 2)Т,
=(3; -2), Ñ f (X)=(4 x 1, 8 x 2)Т,
D X =-[ E -  (A
(A  )
)  A ]Ñ f (X)=-
A ]Ñ f (X)=-  =
=
=-  =-
=-  =
=
=-  =-
=- 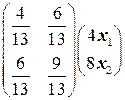 =
=  ,
,
то есть D X »  ,
,
T (X)=- j 1(Xk)=-3 x 1+2 x 2+5,
d 2 X = A T(AA T)  T (X)=
T (X)=  (-3 x 1+2 x 2+5)=
(-3 x 1+2 x 2+5)=
=  (-3 x 1+2 x 2+5)=
(-3 x 1+2 x 2+5)= 
 =
=  ,
,
то есть d 2 X »  .
.
3. Полагаем k =0.
4.0. Проверим выполнение условия k ³ k 0: k =0<10= k 0 - неравенство не выполнено. Поэтому идём к пункту 5.
5.0. Вычисляем матрицу A 0= A (X 0)=(3; -2).
6.0. Вычисляем d 2 X 0=  =
=  .
.
7.0. Вычисляем | d 2 X 0|=  =0.
=0.
8.0. Вычисляем D X 0=  »
»  .
.
9.0. Вычисляем |D X 0|=  »0,832.
»0,832.
10.0. Проверяем выполнение условий |D X 0|£0,1 и | d 2 X 0|£0,1. Имеем |D X 0|>0,1 и | d 2 X 0|£0,1. Поэтому полагаем d 2 X 0=0 и переходим к шагу 11.
11.0. Получим выражение для точки X 0+ h 0D X 0:
X 0+ h 0D X 0=(1; -1)+ h 0(2,462; 3,692)=(1+2,462 h 0; -1+3,692 h 0).
12.0. Определяем h 0 из условия f (X 0+ h 0D X 0)®  . Имеем
. Имеем
f (X 0+ h 0D X 0)=2×(1+2,462 h 0)2+4×(-1+3,692 h 0)2=
=2×(1+4,924 h 0+6,061  )+4×(1-7,384 h 0+13,631
)+4×(1-7,384 h 0+13,631  )=
)=
=66,646  -19,688 h 0+6.
-19,688 h 0+6.
Так как f (X 0+ h 0D X 0) - квадратный трёхчлен относительно h 0 с положительным коэффициентом при  , то минимум f (X 0+ h 0D X 0) достигается при h 0, удовлетворяющем уравнению
, то минимум f (X 0+ h 0D X 0) достигается при h 0, удовлетворяющем уравнению  (X 0+ h 0D X 0)=0. Имеем
(X 0+ h 0D X 0)=0. Имеем
 (X 0+ h 0D X 0)=133,292 h 0-19,688=0 Û h 0»0,15.
(X 0+ h 0D X 0)=133,292 h 0-19,688=0 Û h 0»0,15.
13.0. Вычисляем X 1:
X 1= X 0+ h 0D X 0+ d 2 X 0= X 0+ h 0D X 0=(1+2,462×0,15; -1+3,692×0,15)=(1,3693; -0,4462).
Положим k =1 и перейдём к шагу 4.
4.1. Проверим выполнение условия k ³ k 0: k =1<10= k 0 - неравенство не выполнено. Поэтому идём к пункту 5.
5.1. Вычисляем матрицу A 1= A (X 1)=(3; -2).
6.1. Вычисляем d 2 X 1=  =
=  .
.
7.1. Вычисляем | d 2 X 1|=  »0.
»0.
8.1. Вычисляем D X 1=  »
»  .
.
9.1. Вычисляем |D X 1|=  »0,0677.
»0,0677.
10.1. Проверяем выполнение условий |D X 1|£0,1 и | d 2 X 1|£0,1. Имеем |D X 1|£0,1 и | d 2 X 1|£0,1. Поэтому расчёт окончен. Вычисляем L 1 для проверки необходимых и достаточных условий экстремума в найденной точке X 1=(1,3693; -0,4462):
L 1=-(A 1  )
)  A 1Ñ f (X 1)=
A 1Ñ f (X 1)=  =-1,8135.
=-1,8135.
Выпишем необходимые условия экстремума с учётом функции Лагранжа: L (X, L)=  + l 1(3 x 1-2 x 2-5):
+ l 1(3 x 1-2 x 2-5):
 =4 x 1+3 l 1,
=4 x 1+3 l 1,  =8 x 2-2 l 1,
=8 x 2-2 l 1,
 Û
Û  (4.4.6)
(4.4.6)
Будем считать, что необходимые условия выполнены, если уравнения системы (4.4.6) выполняются с точностью до 0,1. Подставляем X 1=(1,3693; -0,4462) и l 1=-1,8135 в систему (4.4.6):

Следовательно, необходимые условия экстремума в точке X 1 выполнены. Проверим достаточные условия экстремума. Имеем
 =4,
=4,  =8,
=8,  =
=  =0, d 2 L =4 d
=0, d 2 L =4 d  +8 d
+8 d  >0,
>0,
то есть достаточное условие минимума выполняется. Таким образом,
Ответ: точкой условного локального минимума является точка X *»(1,3693; -0,4462), f (X *)»4,5447 - условный локальный минимум.