Билет №16
I. Свойства деления. Правила деления и их связь с вычислительными приемами.
Для действия деления справедливы следующие свойства (законы):
• Деление суммы на число;
• Деление разности на число;
• Деление произведения на число;
• Деление числа на произведение.
Деление суммы на число.
Для любых целых неотрицательных чисел а, b и натурального числа с верно равенство: (а +b): с = а: с + b: с
("а,b ÎNo, с ÎN) (а 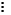 с и в с и в 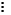 с) Þ (а + b): с = а: с + b: с
В начальной школе знакомство с данным свойством сводится к знакомству с правилом:
Чтобы сумму разделить на число можно на это число разделить каждое слагаемое и полученные результаты (частные) сложить.
Правило «Деление суммы на число» лежит в основе вычислительных приемов деления двузначного числа на однозначное.
Например: 48:4=(40+8):4=40:4+8:4=10+2=12
Рассуждение ученика: представляю число 48 в виде суммы разрядных слагаемых 40 и 8, нам удобно сначала каждое слагаемое разделить на 4 затем сложить полученные результаты, (частные) 10 и 2 и получить 12.
Деление разности на число
Для любых целых неотрицательных чисел а,b и натурального числа с верно равенство:
(а - b): с = а: с + b: с
("а,b ÎNo, с ÎN) (а с) Þ (а + b): с = а: с + b: с
В начальной школе знакомство с данным свойством сводится к знакомству с правилом:
Чтобы сумму разделить на число можно на это число разделить каждое слагаемое и полученные результаты (частные) сложить.
Правило «Деление суммы на число» лежит в основе вычислительных приемов деления двузначного числа на однозначное.
Например: 48:4=(40+8):4=40:4+8:4=10+2=12
Рассуждение ученика: представляю число 48 в виде суммы разрядных слагаемых 40 и 8, нам удобно сначала каждое слагаемое разделить на 4 затем сложить полученные результаты, (частные) 10 и 2 и получить 12.
Деление разности на число
Для любых целых неотрицательных чисел а,b и натурального числа с верно равенство:
(а - b): с = а: с + b: с
("а,b ÎNo, с ÎN) (а 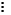 с и в с и в 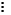 с) Þ (а - b): с = а: с - b: с
Данное свойство можно сформулировать в виде правила: Чтобы разность разделить на число можно на это число сначала разделить уменьшаемое, затем вычитаемое и из первого результата (частного) вычесть второй.
В начальной школе дети специально не знакомятся с данным правилом, но при выполнении некоторых заданий сталкиваются с его применением.
Например: сравни выражения (18-6):3 > 18:3-6. Выполняя это задание дети могут применить правило для выражения стоящего в левой части (18-6):3=18:3-6:3 и сравнив полученные выражения с выражениями стоящими в правой части, проанализировав отличия: 18:3-6 уменьшаемое 18:3, вычитаемое 6, следовательно, разность меньше и левая часть больше правой.
Деление произведения на число
Для любых целых неотрицательных чисел а,b и натурального числа с верно равенство: (а × b): с =(а: с) × b =(b: с) × а
(" а,b ÎNo, с ÎN) (а с) Þ (а - b): с = а: с - b: с
Данное свойство можно сформулировать в виде правила: Чтобы разность разделить на число можно на это число сначала разделить уменьшаемое, затем вычитаемое и из первого результата (частного) вычесть второй.
В начальной школе дети специально не знакомятся с данным правилом, но при выполнении некоторых заданий сталкиваются с его применением.
Например: сравни выражения (18-6):3 > 18:3-6. Выполняя это задание дети могут применить правило для выражения стоящего в левой части (18-6):3=18:3-6:3 и сравнив полученные выражения с выражениями стоящими в правой части, проанализировав отличия: 18:3-6 уменьшаемое 18:3, вычитаемое 6, следовательно, разность меньше и левая часть больше правой.
Деление произведения на число
Для любых целых неотрицательных чисел а,b и натурального числа с верно равенство: (а × b): с =(а: с) × b =(b: с) × а
(" а,b ÎNo, с ÎN) (а 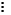 с) Þ (а × b): с =(а: с) × b
(" а,b ÎNo, с ÎN) (в с) Þ (а × b): с =(а: с) × b
(" а,b ÎNo, с ÎN) (в 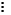 с) Þ (а × b): с =(b: с) × а
Данное свойство можно сформулировать в виде правила: Чтобы произведение разделить на число можно на это число разделить один из множителей и полученный результат (частное) умножить на второй множитель.
Деление числа на произведение
Для любых целых неотрицательных чисел а, b и натурального числа с верно равенство: а:(b × с) =(а: b): с =(а: с): b
(" а ÎNo, b, с ÎN) а:(b × с) =(а: b): с =(а: с): b
Данное свойство можно сформулировать в виде правила:
Чтобы число разделить на произведение можно это число разделить сначала на один из множителей и полученный результат (частное) разделить на другой множитель.
Эти правила лежат в основе вычислительных приемов деления чисел, оканчивающихся нулями.
Например: 480:6=(48·10):6=(48:6)·10=8·10=80 в основе решения лежит правило деления произведения на число.
II. Разработать фрагмент урока по ознакомлению учащихся с одним из свойств деления.
Повторить понятия суммы, частного, слагаемое, таблицу умножения.
Для знакомства с правилом деления суммы на число можно предложить детям задачу, имеющую два способа решения. Числа в условии подбирают так, чтобы все вычисления проходили в пределах таблицы умножения и соответствующих случаев деления.
Например: Двум мальчикам раздали 4 пирожных и по 6 конфет, так что у каждого получилось сладостей поровну. Сколько сладостей получил каждый?
1 способ. Сколько всего было сладостей? (4+6=10) Сколько сладостей получил каждый мальчик? (10:2=5) (равенство (4+6):2=5)
2 способ: Сколько пирожных получил каждый мальчик (4:2=2) Сколько конфет получил каждый мальчик? (6:2=3) Сколько сладостей всего получил каждый? (5) (равенство (4:2) + (6:2)=5)
Дети находят сходства (одинаковые числа, действия и ответы, различия (порядок выполнения действий). Вспомнив название выражения (1способ) записанного в скобках (4+6) и названия чисел при сложении (1 и 2 слагаемое) младшие школьники формулируют правило деление суммы на число с) Þ (а × b): с =(b: с) × а
Данное свойство можно сформулировать в виде правила: Чтобы произведение разделить на число можно на это число разделить один из множителей и полученный результат (частное) умножить на второй множитель.
Деление числа на произведение
Для любых целых неотрицательных чисел а, b и натурального числа с верно равенство: а:(b × с) =(а: b): с =(а: с): b
(" а ÎNo, b, с ÎN) а:(b × с) =(а: b): с =(а: с): b
Данное свойство можно сформулировать в виде правила:
Чтобы число разделить на произведение можно это число разделить сначала на один из множителей и полученный результат (частное) разделить на другой множитель.
Эти правила лежат в основе вычислительных приемов деления чисел, оканчивающихся нулями.
Например: 480:6=(48·10):6=(48:6)·10=8·10=80 в основе решения лежит правило деления произведения на число.
II. Разработать фрагмент урока по ознакомлению учащихся с одним из свойств деления.
Повторить понятия суммы, частного, слагаемое, таблицу умножения.
Для знакомства с правилом деления суммы на число можно предложить детям задачу, имеющую два способа решения. Числа в условии подбирают так, чтобы все вычисления проходили в пределах таблицы умножения и соответствующих случаев деления.
Например: Двум мальчикам раздали 4 пирожных и по 6 конфет, так что у каждого получилось сладостей поровну. Сколько сладостей получил каждый?
1 способ. Сколько всего было сладостей? (4+6=10) Сколько сладостей получил каждый мальчик? (10:2=5) (равенство (4+6):2=5)
2 способ: Сколько пирожных получил каждый мальчик (4:2=2) Сколько конфет получил каждый мальчик? (6:2=3) Сколько сладостей всего получил каждый? (5) (равенство (4:2) + (6:2)=5)
Дети находят сходства (одинаковые числа, действия и ответы, различия (порядок выполнения действий). Вспомнив название выражения (1способ) записанного в скобках (4+6) и названия чисел при сложении (1 и 2 слагаемое) младшие школьники формулируют правило деление суммы на число
| Билет №17
I. Алгоритм письменного деления. Последовательность изучения в начальной школе.
Алгоритм письменного деления изучается последовательно:
Деление на однозначное число.
1. Деление на однозначное число сначала рассматривают случаи, когда каждая цифра делимого делится на делитель. То есть когда в частном столько же цифр сколько и в делимом. Например: 936: 3; 468: 2, 684: 4;
2. Деление на однозначное число, когда в частном цифр меньше чем в делителе. Дети учатся определять количество цифр в частном.Например:268:4
3. Деление на однозначное число, когда одна из цифр частного равна 0. Например: 828:4
Деление на числа оканчивающиеся нулями без остатка и с остатком 8240:80
Деление на двузначное и многозначное число.
1. сначала рассматривают случаи деления на круглое число с остатком, когда в частном получается одна цифра. Например: 638: 90; 7350: 800;
2. затем случаи деления на круглое число без остатка и в частном получается более одной цифры. Например: 3240: 60; 5920: 80;
3. после этого рассматривают случаи деления многозначного числа на многозначное, когда в частном получается сначала одна цифра, например: 432: 72; 294: 42; затем более одной цифры,
например: 828: 36; 4725: 63;
4. наконец рассматривают случаи, когда в частном получаются нули. Сначала без остатка, например: 132192: 324; 272640: 284, а затем с остатком, например: 37971: 73;
Алгоритм деления на примере 4725:63.
Запишем числа уголком. Найдем первое неполное делимое и определим количество цифр в частном. В делители две цифры. Берем две первые слева цифры. Получим число 47. 47 меньше 63, поэтому берем слева три цифры и получаем 472, первое неполное делимое. 472 это полное число десятков в числе 4725, следовательно в ответе у нас будут десятки и единицы - 2 цифры. Подбираем первую цифру частного способом округления. Округлим делитель 63 до числа 60. 472 разделим на 60=6*10, для этого сначала разделим на 10 и получим 47, а потом 47 разделим на 6 и получим 7. Проверяем полученную цифру 7, для этого 63 умножим на 7 и получим 441, 441 меньше 472, найдем остаток 472-441=31, остаток меньше делителя, значит цифра подобрана верно и ее можно записать в ответ. Припишем к поученному остатку следующую цифру делимого. Получается неполное делимое 315, она больше 63. Подбираем следующую цифру частного по последней цифре. Последняя цифра делимого равна 5, значит вероятнее всего цифра частного будет 5. Проверяем полученную цифру. Для этого 63 умножим на 5 и получим 315, значит цифра верна и ее можно записать в ответ. Получилось 75.
Существую различные способы для деления:
1 Способ округления
2 Использование результатов предыдущих подборов
3 Подбор цифр частного по последним цифрам делимого и делителя.
II. Разработать фрагмент урока по ознакомлению учащихся с письменным приемом деления на однозначное число.
Повторить разряды, таблицу умножения, правило записи деления уголком, повторить алгоритм деления, упражнения для закрепления материала.
При изучении письменного деления на однозначное число ученики должны усвоить алгоритм деления — уметь образовывать неполные делимые, устанавливать число цифр частного, понимать смысл каждой вычислительной операции: неполное делимое делится на делитель для того, чтобы найти соответствующую цифру частного; найденную цифру частного умножают на делитель для того, чтобы узнать, сколько соответствующих единиц разделили; полученное число вычитают для того, чтобы узнать, сколько соответствующих единиц осталось разделить и правильно ли подобрана цифра частного.
Вначале письменное деление на однозначное число учащиеся выписывают подробно и объясняют следующим образом:
 1.Делимое 2916. Делитель 6
1.Делимое 2916. Делитель 6
 Высший разряд делимого — тысячи; две тысячи нельзя разделить на 6 равных частей так, чтобы в каждой части получилось хотя бы по одной тысяче. Раздробим 2 тысячи в сотни и прибавим 9 сотен, получим 29 сотен. Это число делится на 6 равных частей так, что в.каждой части получаются сотни. Значит, высший разряд частного — сотни. Сотни стоят на третьем месте справа, значит, в частном будут три цифры. Вместо трех цифр пока ставим три точки.
29 сотен разделим на 6, получим 4 сотни.
Узнаем, сколько всего сотен мы разделили. Для этого умножим 4 сотни на 6, получим 24 сотни.
Узнаем, сколько сотен осталось разделить. Для этого отнимем 24 сотни от 29 сотен, получим 5 сотен.
Остаток 5 сотен не делится на 6, следовательно, цифра частного подобрана правильно.
Раздробим 5 сотен в десятки, получим 50 десятков.
Прибавим 1 десяток, получим 51 десяток.
51 десяток разделим на 6, получим 8. И т. д.
Частное — 486. Важно, чтобы при делении ученики записывали каждую цифру в своей клетке. Аккуратные записи вообще, а при делении особенно сокращают число ошибок. Высший разряд делимого — тысячи; две тысячи нельзя разделить на 6 равных частей так, чтобы в каждой части получилось хотя бы по одной тысяче. Раздробим 2 тысячи в сотни и прибавим 9 сотен, получим 29 сотен. Это число делится на 6 равных частей так, что в.каждой части получаются сотни. Значит, высший разряд частного — сотни. Сотни стоят на третьем месте справа, значит, в частном будут три цифры. Вместо трех цифр пока ставим три точки.
29 сотен разделим на 6, получим 4 сотни.
Узнаем, сколько всего сотен мы разделили. Для этого умножим 4 сотни на 6, получим 24 сотни.
Узнаем, сколько сотен осталось разделить. Для этого отнимем 24 сотни от 29 сотен, получим 5 сотен.
Остаток 5 сотен не делится на 6, следовательно, цифра частного подобрана правильно.
Раздробим 5 сотен в десятки, получим 50 десятков.
Прибавим 1 десяток, получим 51 десяток.
51 десяток разделим на 6, получим 8. И т. д.
Частное — 486. Важно, чтобы при делении ученики записывали каждую цифру в своей клетке. Аккуратные записи вообще, а при делении особенно сокращают число ошибок.
| Билет №18
I. Длина отрезка. Единицы измерения длины и их соотношения
Длиной отрезка называется неотрицательная скалярная величина, обладающая следующими свойствами:
Равные отрезки имеют равные длины.
Если отрезок состоит из конечного числа отрезков, то его длина равна сумме этих отрезков.
Термин «длина» употребляется для обозначения свойства, либо класса объектов, либо конкретного объекта из этого класса.
При решении практических задач используются стандартные единицы длины: миллиметр, сантиметр, метр, километр и др.
Изучение данного вопроса в начальной школе идет с опорой на базовые (бытовые представлениия) знания детей о длине. Также в н. ш. дети знакомятся с историей развития мер длины (рассматриваются такие меры как локоть, сажень, вершок, аршин, дюйм, верста и др.).
Выявление и уточнение представление детей о длине. Это удобно сделать в форме фронтальной беседы или опроса.
Знакомство с единицей измерения данной величины и измерительным прибором. Дети убеждаются в необходимости введения единой единицы измерения длины. При изучении данной темы превалирует практический метод.
Формирование измерительных умений и навыков у учащихся. Осуществляется на практических занятиях.
Сложение и вычитание однородных величин, выраженных в одной единице измерения. Например: М2 (1-4) с.13. №5. с.15. №4.
Знакомство с новой единицей измерения данной величины. Для этого дети в ходе практической деятельности убеждаются в необходимости введения новой единицы измерения длины, для удобства выполнения измерений.
Сложение и вычитание величин, выраженных в 2х единицах наименования. Для усвоения соотношения между единицами длины предлагаются упражнения:
на измерение;
на построение отрезков определенной длины, выраженной в единицах 2х наименований;
на перевод величины, выраженной в одной единицы измерения, в другие единицы измерения;
на сравнение однородных величин.
Умножение и деление величины на число. Например: М4(1-4) с. 66. №299.
В 1 классе учитель учит детей сравнивать длины непосредственно. Со с.41. М1 вводится опосредованное сравнение длин. Со с.120. М1. вводится понятие сантиметр. Изучение тем длина отрезка в н. ш. Идет параллельно с изучением темы нумерация. При изучении концентра 100 появляется новые единицы измерения – дециметр и метр. При изучении концентра 1000 – километр. Изучение темы километр целесообразно подкреплять экскурсией (прохождение заранее отмеренного расстояния).
Задача учителя показать детям значимость появления новой единицы измерения длины.
Цели изучения данного материала в н. ш. разнообразны:
Бытовая необходимость.
Прикладная необходимость
Интеллектуальное развитие мл. шк. (разв. мышления и воссоздающего воображения).
Изучение данного материала способствует и дальнейшему успешному обучению в старших классах по предмету геометрии.
1км = 1000 м, 1 м = 10 дм, 1 дм = 10 см, 1 см = 10 мм
Учитель предлагает:- Сравните длину ручки и длину карандаша на вашем столе. Что
вы можете сказать? (Ручка длиннее карандаша; или карандаш
длиннее ручки; или одинаковые по длине.)- Как вы это узнали? (Приложили их друг к другу.)У детей на каждой парте лежит набор полосок бумаги.
- Возьмите синюю и красную полоски. Сравните их по ширине и длине.
Как это сделать? (Наложить полоски друг на друга.)- Наложите полоски друг на друга. Что мы видим? (Мы видим, что одна полоска шире, другая уже.) Затем можно предложить сравнить по картинке длину ручки и кисточки (ручка короче, кисточка длиннее), сравнить длину красного карандаша и ручки (красный карандаш короче, ручка длиннее).- Как сравнить? В данной ситуации дети используют сравнение длин предметов «на глаз», т.к. изображения нельзя сравнить ни наложением, ни приложением. Чтобы подвести детей к тому, что можно сравнивать предметы с помощью мерки, можно предложить следующее задание: «Вова начертил полоски. Помоги ему сравнить их по длине.» - Как сравнить длины полосок, изображенных на рисунке? Можно наложить их друг на друга? (Нет, сделать этого нельзя, они нарисованы.)- Что вам может помочь сравнить эти полоски? (Они нарисованы
на бумаге в клетку.)- Сколько клеток помещается в красной полоске? (Синей? Желтой? Зеленой?)- Какая полоска самая длинная? (Желтая полоска, т.к. в ней помещается пять клеток.)- Какая полоска самая короткая? (Синяя полоска, в ней помещается три клетки.)- Что нам помогло сравнить полоски? (Клеточки.)
Далее учитель показывает модель 1 сантиметра и сообщает, что это мерка длины и называется она сантиметр. Учащиеся рассматривают модель мерки, равную 1 сантиметру. В учебнике предлагается задание: Измерь длину отрезка в сантиметрах. Затем, учащиеся знакомятся с измерительным прибором. Учитель сообщает, что для измерения длины используется специальный инструмент – линейка. Учащиеся учатся работать с линейкой.
| Билет №19
Масса тела. Единицы измерения массы тела и их соотношения
Масса – физическая величина, отвечающая способности физических тел сохранять своё поступательное движение (инертность). Масса – фундаментальная физическая величина, определяющая инертные и гравитационные свойства всех тел до атомов и элементарных частиц.
Масса тела – это фундаментальная физическая величина, определяющая инерционные и гравитационные свойства тел (от макроскопических тел до атомов и элементарных частиц), свойство сохранять приобретенноедвижение
или состояние покоя. Под массой понимают 2 различных свойства физического объекта: гравитационная масса – показывает с какой силой тело взаимодействует с внешними гравитационными полями, и инертная масса – характеризует меру инертности тел. Свойства массы: сравнимость, складываемость (в результате сложения двух величин одного рода получается величина того же рода), умножение на число, вычитаемость, деление на число.
1 тонна = 10 центнерам, 1 центнер = 100 кг, 1 кг = 1000 гр
2.На столе учителя стоят две одинаковые по цвету и форме коробки, но одна коробка пустая, а в другую положен какой-то тяжелый предмет.- Сравните эти коробки. (Они одинаковые по цвету, по форме.)- Есть ли отличие у этих коробок? (Нет.) И все-таки учитель отмечает: различие между ними существует. Учащиеся столкнулись с проблемной ситуацией. Учитель побуждает их к формулированию проблемы.
- Какой возникает вопрос? (Чем отличаются эти коробки?)- Какая коробка легче?
- Какая тяжелее?- Отличие ли это – быть легче или тяжелее другого предмета? (Да,
14это новый признак (свойство).- А кто знает, как называется это свойство? (Масса.)
- С помощью какого прибора измеряется масса? (С помощью весов.)
Следующая ситуация поможет ввести мерку массы килограмм. Учащимся предлагается задание сравнить массу дыни и массу пакета риса.
 Создалась проблемная ситуация.
- Можно ли выполнить это задание? (Нет.) - В чем затруднение? (Использовались разные мерки. яблоки и бананы) Для выхода из проблемной ситуации учитель задает вопрос:- Что нужно сделать, чтобы это задание можно было выполнить?(Использовать одинаковую мерку.)- Существует единая мерка для нахождения массы. Кто из вас знает, как эта мерка называется? (Килограмм.)Учитель показывает гирю – 1 килограмм.
- Можем мы теперь выполнить задание? Учащиеся находят массу дыни, массу пакета риса и сравнивают
их.
Создалась проблемная ситуация.
- Можно ли выполнить это задание? (Нет.) - В чем затруднение? (Использовались разные мерки. яблоки и бананы) Для выхода из проблемной ситуации учитель задает вопрос:- Что нужно сделать, чтобы это задание можно было выполнить?(Использовать одинаковую мерку.)- Существует единая мерка для нахождения массы. Кто из вас знает, как эта мерка называется? (Килограмм.)Учитель показывает гирю – 1 килограмм.
- Можем мы теперь выполнить задание? Учащиеся находят массу дыни, массу пакета риса и сравнивают
их.
|
|
Билет №20
I. Площадь фигуры. Единицы измерения площади их соотношения
Каждый человек представляет, что такое площадь комнаты, площадь участка земли, площадь поверхности, которую надо покрасить. Он также понимает, что если земельные участки одинаковы, то площади их равны; что площадь квартиры складывается из площади комнат и площади других ее помещений. Это обыденное (бытовое) представление о площади используется при ее определении в геометрии, где говорят о площади фигуры.
Но геометрические фигуры устроены по-разному, и поэтому, когда говорят о площади, выделяют определенный класс фигур. Например, рассматривают площади многоугольных фигур или площади криволинейных фигур и т.д. Мы будем рассматривать понятие площади применительно к многоугольникам и ограниченным плоским фигурам.
Если говорят, что фигура F состоит (составлена) из фигур F1 и F2, то имеют в виду, что она является их объединением, и у них нет общих внутренних точек. В этой же ситуации говорят, что фигура F разбита на фигуры F1 и F2 и пишут F=F1+F2. Например, о фигуре F, изображенной на рисунке 1,можно сказать, что она составлена из фигур F1 и F2 или что она разбита на фигуры F1 и F2.
Определение. Площадью фигуры называется неотрицательная скалярная величина, определенная для каждой фигуры так, что:
1) равные фигуры имеют разные площади;
2) если фигура состоит из двух частей, то ее площадь равна сумме площадей этих частей.
Эти свойства площади фигуры используются при ее измерении. Чтобы измерить площадь фигуры, нужно иметь единицу площади. Как правило, такой единицей является площадь квадрата со стороной, равной единичному отрезку. Условимся площадь единичного квадрата обозначать буквой Е. Результатом измерения площади фигуры F будет неотрицательное действительное число, обозначим его S(F). Это число называют численным значением площади фигуры F при выбранной единице площади Е. В геометрии доказано, что для многоугольника и ограниченных плоских фигур такое число всегда существует и оно единственно. Из определения площади следуют известные свойства численных значений площади. Сформулируем некоторые их них, считая, что единица площади выбрана.
1. Если фигуры равны, то равны и численные значения их площадей, т.е. F1=F2ÞS(F1) = S(F2). Фигуры, у которых площади равны, называются равновеликими.
2. Если фигура F состоит из фигур F1 и F2 то численное значение площади фигуры равно сумме численных значений площадей фигур F1 и F2, т.е. S(F1+F2)=S(F1)+S(F2).
3. Численное значение площади единичного квадрата принимается равным 1,т.е. S(E) =1.
4. При замене единицы площади численное значение площади фигуры F увеличивается (уменьшается) во столько раз, во сколько раз новая единица меньше (больше) старой.
5. Если фигура F1 является частью фигуры F2,то численное значение площади фигуры F1 не больше численного значения площади фигуры F2, т.е. F1≤F2 Þ S(F1) ≤ S(F2).
В практической деятельности при измерении площадей используются стандартные единицы площади: квадратный метр (кв.м.), квадратный сантиметр (кв.см.) и другие. Так, квадратный метр – это площадь квадрата со стороной, равной 1 метру. Между единицами площади существует взаимосвязь. Например, 1кв.м.=100кв.дм.
Формулы для вычисления площади прямоугольника, треугольника, параллелограмма были выведены давно. В геометрии их обосновывают, исходя из определения площади, при этом численное значение площади называют площадью, а численное значение длины отрезка – длиной.
Так как теоремы о площади прямоугольника, параллелограмма, треугольника хорошо известны из школьного курса математики, то рассмотрим только теорему о площади прямоугольника, доказав ее для случая, когда длины его сторон выражены натуральными числами. Такой выбор обусловлен тем, что знакомство с правилом вычисления площади прямоугольника происходит в начальной школе.
Теорема. Площадь прямоугольника равна произведению длин его соседних сторон.
Напомним, что слово “площадь” в этой формулировке означает численное значение площади, а слово “длина” – численное значение длины отрезка. Из этой теоремы вытекает следствие: площадь прямоугольного треугольника равна половине произведения его катетов.
Пусть F – некоторая криволинейная фигура. Как найти ее площадь? Оказывается это можно сделать с помощью площадей многоугольных фигур. Мы рассмотрим способ, который используется в начальном обучении.
Если многоугольная фигура Q содержит фигуру F, а многоугольная фигура Р содержится в фигуре F, т.е. QÎFÎP, то S(P)≤S(F)≤S(Q). Если разность площадей фигур Q и P стремится к нулю, то существует единственное число S(F), удовлетворяющее данному неравенству и его считают площадью фигуры F.
Мы воспользуемся этим положением для обоснования приема измерения площади фигуры при помощи палетки. Палетка – это прозрачная пластина, на которой нанесена сеть квадратов. Сторона квадрата принимается за 1, и чем меньше эта сторона, тем точнее можно измерить площадь фигуры.
Накладываем палетку на данную фигуру F. Квадраты, которые целиком лежат внутри фигуры F, образуют многоугольную фигуру Р; квадраты, имеющие с фигурой F общие точки, образуют многоугольную фигуру Q. Площади S(P) и S(Q) находят простым подсчетом квадратов. За приближенное значение площади фигуры F принимается среднее арифметическое найденных площадей:
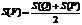
В начальном курсе математики учащиеся измеряют площади фигур с помощью палетки таким образом: подсчитывают число квадратов, которые лежат внутри фигуры F, и число квадратов, через которые проходит контур фигуры; затем второе число делят пополам и прибавляют к первому. Полученную сумму считают площадью фигуры F. Нетрудно обосновать эти действия. Пусть m – число квадратов, которые поместились внутри фигуры F, а n – число квадратов, через которые проходит контур фигуры F. Тогда S(P)=m, a S(Q)=m+n. И значит:

Палетка позволяет измерить площадь фигуры F с определенной точностью. Чтобы получить более точный результат, нужно взять палетку с более мелкими квадратами. Но можно поступить иначе: наложить одну и ту же палетку по-разному на фигуру и найти несколько приближенных значений площади фигуры F. Их среднее арифметическое может быть лучшим приближением к численному значению площади фигуры F.
1 гектар = 100 арам = 10 000 м2
1 ар = 100 м2
1 км2 = 1 000 000 м2
1 м2 = 100 дм2 = 10 000 см2
Длины сторон прямоугольника 4 см и 3 см. Чему равна его площадь?)
– На сколько строчек (столбиков) разбит прямоугольник?– Сколько см2 умещается в каждой из них?
– Как же узнать, сколько всего кв. см помещается в прямоугольнике, т.е. какова площадь этого прямоугольника? (3•4=12(см2) или 4•3=12(см2)
– Объясните, почему записали такое равенство? (В каждой строке 4 см2, таких строчек 3, по 4 взять 3 раза – 4•3, получится 12 см2,или
В каждом столбике 3 см2, таких столбиков 4, по 3 взять 4 раза – 3•4, получится 12 см2)
– Каким же действием узнавали площадь прямоугольника? (Умножением)
– Какие числа перемножали? (3 и 4)
– Что выражают эти числа? (длины сторон; длину и ширину)
– Сделайте вывод, как же найти площадь прямоугольника? (Чтобы найти площадь прямоугольника, надо умножить длины сторон)
– Как можно сказать по-другому, чему равна площадь прямоугольника? (Площадь прямоугольника равна произведению длин сторон)– Как это правило можно записать в виде буквенного равенства? (S = a•b)
– Это равенство в математике называют формулой. Ее можно использовать для вычисления площади любого прямоугольника.– Как удобнее узнавать площадь прямоугольника: с помощью мерок или пользуясь формулой? Почему? (С помощью формулы быстрее; если длины сторон выражены в метрах, то не сможем начертить)
| Билет №21
I. Время. Единицы измерения времени и их соотношения.
Вре́мя — одно из основных понятий философии и физики, условная сравнительная мера движения материи, а также одна из координатпространства-времени
, вдоль которой протянуты мировые линии физических тел. В курсе математики начальных классов дети знакомятся с различными величинами: длина, масса, объем, время, площадь.
Изучение величин тесно связано с изучением нумерации, т.к. способствует формированию у учащихся представлений о числе и зависимости между единицами измерения также, как между разрядными единицами при счете:1дм.=10см, 1дес.=10ед. и т.п.
При формировании представлений о каждой из названных величин целесообразно ориентироваться на определенные этапы, в которых нашли отражение: математическая трактовка данного понятия, его взаимосвязь с изучением других вопросов начального курса математики, а также психологических особенностей младших школьников:
1этап. Выяснение и уточнение представлений школьников о данной величине (обращение к опыту ребенка).
2 этап. Сравнение однородных величин(визуально, с помощью ощущений, наложением, приложением, путем использовании различных мерок)
3этап. Знакомство с единицей данной величины и с измерительным прибором.
4этап. Формирование измерительных умений и навыков.
5этап. Сложение и вычитание однородных величин, выраженных в единицах одного наименования.
6этап. Знакомство с новыми единицами величин в тесной связи с изучением нумерации и сложения чисел. Перевод однородных величин, выраженных в единицах одного наименования, в величины, выраженные в единицах двух наименований, и наоборот.
7этап. Сложение и вычитание величин, выраженных в единицах двух наименований.
8этап Умножение и деление величин на число.
1 сутки = 24 часа, 1 час = 60 минут, 1минута = 60 секунд
Единицы измерения времени
- Тысячелетие (Миллениум) - 1000 лет
- Век - 100 лет
- Индикт - 15 лет
- Десятилетие - 10 лет
- Год - 365 суток
- Квартал - 3 месяца - 1/4 года
- Месяц - 3 декады - 30 суток
- Декада - 10 суток
- Неделя - 7 суток
- Сутки 1/7 недели
- Час 1/24 суток
- Минута 1/60 часа
- Секунда 1/60 минуты
- Кадр - 1/25 секунды
- Терция — 1/60 секунды
Во 2 классе при введении величины «время» и ее мерки –час, можно сначала предложить решить задачи. Например:1). Для поездки на работу Катиной маме требуется 1 час, а папе –2 часа. Чья поездка занимает больше времени и на сколько? 2). Чтобы очистить овощи и подготовить продукты для приготовления обеда, Катиной бабушке нужен час и столько же времени требуется, чтобы сварить еду. Сколько всего времени нужно Катиной бабушке, чтобы приготовить обед?
Затем, можно задать вопросы:- Можно ли сказать, что время – это величина?- Какие единицы измерения времени вы знаете?- Какой прибор служит для измерения времени? 2.В 3 классе учащиеся знакомятся с новыми единицами измерения времени - год, месяц, неделя, сутки, календарь. При знакомстве с сутками, учащимся можно предложить
следующее задание: «В течение дня Ваня сделал несколько рисунков. Какое время показывают стрелки механических часов на рисунках Вани?»- Можете ли вы сказать, глядя на рисунки, утром или вечером они сделаны? - Как называется общая продолжительность дня и ночи? (Сутки.)
При знакомстве с календарем, можно предложить задать вопрос учащимся:
- Как вы думаете, на какой день недели придется в этом году начало летних каникул? При введении следующей мерки – секунды, можно предложить такую ситуацию. Детям предлагается прослушать две мелодии. Одна, из них длится 1 минуту, а другая мелодия - 55 секунд. После прослушивания детям задается вопрос:- Какая мелодия длилась дольше?Учитель создал проблемную ситуацию. Учащиеся затруд-няются ответить.- Во время прослушивания мелодии сосчитайте, сколько раз будет двигаться стрелка на часах. В процессе этой работы дети выясняют, что при прослушивании первой мелодии стрелка двигалась 60 раз и прошла полный круг, т.е. мелодия длилась одну минуту. Вторая мелодия длилась меньше, т.к. пока она звучала, стрелка двигалась 55 раз.
- Как называется каждый «шажок» стрелки? (Секунда.)- Сколько «шажков» совершает стрелка, проходя полный круг? (Стрелка, проходя полный круг - минуту - совершает 60 «шагов».)- Какой можно сделать вывод? (В одной минуте 60 секунд.)Далее учитель сообщает, что стрелка, которой они пользовались, называется секундной, а стрелка, которая меньше секундной, указывает на минуты.
При знакомстве с веком, учащимся предлагается выполнить задание: Катя и Саша записали все известные им единицы измерения. На какие группы их можно разбить?
Литр, секунда, минута, дециметр, квадратный метр, месяц, час,
миллиметр, метр, сутки, килограмм, неделя, год, век.
- Назовите все известные вам элементы множеств «Единицы вре-
мени», «Единицы длины», «Единицы емкости», «Единицы мас-
сы», «Единицы площади».- Все ли меры времени, записанные здесь, вам знакомы?
- Знаете ли вы, сколько лет длится век?- Какие промежутки времени измеряют веками. Какой вывод можно сделать?
ознакомлению учащихся с порядком выполнения арифметических действий.
| Билет №22
Понятие числового выражения. Способы нахождения значения числового выражения.
Записи виды 5+3, 728:6,  - называются числовыми выражениями. Т.об. ч.в. содержит числа и знаки математических действий.
В нач. шк. ч.в. содержат действия +, -, ·,:. Ч.в. может содержать одно или несколько действий, а также (), определяющие порядок выполнения этих действий, напр. (5+3)·4. Если выполнить все действия в указанном порядке, то в результате получается число, к-ое называется значением ч.в., напр. (2+3)·1= 5.
Название ч.в. определяется последним действием, напр. (3 + 5)·2; 3+5 · 2. При чтении ч.в. используются названия компонентов и название действий, напр. (2+3).
При нахождении значения выражений применяется правило порядка выполнения действий:
1.Если выражение содержит только действия сложение и вычитание или только действия умножение и деление, то действия в выражении могут выполняться по порядку.
2.Если выражение содержит одновременно действия сложения или вычитания, а также действия умножение или деление, то сначала выполняются действия умножение и деление по порядку, а затем сложение и вычитание по порядку.
3.Если выражение содержит скобки, то сначала выполняются действия в скобках с учетом правил 1 и 2, а потом все остальные действия с учетом этих же правил.
Разработать фрагмент урока по ознакомлению учащихся с порядком выполнения арифметических действий.
Порядок выполнения арифметических действий в выражении — это последовательность проводимых вычислений в данном выражении.
Правила о порядке выполнения арифметических действий вводятся постепенно, начиная с 1 класса, когда дети имеют дело с выражениями, содержащими только сложение и вычитание. Здесь они усваивают, что действия выполняются в том порядке, как они записаны: слева направо. Во 2 классе вводятся скобки как знаки, указывающие на изменение порядка выполнения действий. Правила о порядке выполнения действий усложняются при ознакомлении с умножением и делением в теме «Числа от 1 до 100». В дальнейшем, на последнем году обучения в начальной школе, рассматриваются новые для учащихся правила о порядке выполнения действий в выражениях, содержащих две пары скобок или два действия внутри скобок. Эти правила иллюстрируются довольно сложными примерами, содержащими сначала 2—3, а затем 3—4 арифметических действия.
В результате дети должны освоить следующее правила: - называются числовыми выражениями. Т.об. ч.в. содержит числа и знаки математических действий.
В нач. шк. ч.в. содержат действия +, -, ·,:. Ч.в. может содержать одно или несколько действий, а также (), определяющие порядок выполнения этих действий, напр. (5+3)·4. Если выполнить все действия в указанном порядке, то в результате получается число, к-ое называется значением ч.в., напр. (2+3)·1= 5.
Название ч.в. определяется последним действием, напр. (3 + 5)·2; 3+5 · 2. При чтении ч.в. используются названия компонентов и название действий, напр. (2+3).
При нахождении значения выражений применяется правило порядка выполнения действий:
1.Если выражение содержит только действия сложение и вычитание или только действия умножение и деление, то действия в выражении могут выполняться по порядку.
2.Если выражение содержит одновременно действия сложения или вычитания, а также действия умножение или деление, то сначала выполняются действия умножение и деление по порядку, а затем сложение и вычитание по порядку.
3.Если выражение содержит скобки, то сначала выполняются действия в скобках с учетом правил 1 и 2, а потом все остальные действия с учетом этих же правил.
Разработать фрагмент урока по ознакомлению учащихся с порядком выполнения арифметических действий.
Порядок выполнения арифметических действий в выражении — это последовательность проводимых вычислений в данном выражении.
Правила о порядке выполнения арифметических действий вводятся постепенно, начиная с 1 класса, когда дети имеют дело с выражениями, содержащими только сложение и вычитание. Здесь они усваивают, что действия выполняются в том порядке, как они записаны: слева направо. Во 2 классе вводятся скобки как знаки, указывающие на изменение порядка выполнения действий. Правила о порядке выполнения действий усложняются при ознакомлении с умножением и делением в теме «Числа от 1 до 100». В дальнейшем, на последнем году обучения в начальной школе, рассматриваются новые для учащихся правила о порядке выполнения действий в выражениях, содержащих две пары скобок или два действия внутри скобок. Эти правила иллюстрируются довольно сложными примерами, содержащими сначала 2—3, а затем 3—4 арифметических действия.
В результате дети должны освоить следующее правила:
- а) если в выражении только действия сложение и вычитание, то вычислять нужно по порядку;
- б) если в выражении действия и сложение, и вычитание, и умножение и деление, то сначала выполняются действия умножение и деление по порядку, затем - действия сложение и вычитание по порядку;
- в) если в выражении встречаются скобки, то сначала производятся вычисления в скобках (или скобки раскрываются), а затем вне скобок, согласно первым двум правилам.
Порядок выполнения действий один и для числовых выражений, и для буквенных выражений.
Урок по теме: «Запись и чтение выражений со скобками, правило порядка выполнения действий в выражениях со скобками». (2 класс)
Для подготовки к восприятию нового материала необходимо повторить название компонентов при сложении и вычитании.
Например, детям предлагаются такие задания:
1.
Записать и найти сумму чисел: 5 и 8, 10 и 7, 3 и 6.
Записать и найти разность чисел 10 и 7, 3 и 5.
Уменьшаемое – 8, вычитаемое – 2, найти разность.
Первое слагаемое – 6, второе слагаемое – 4, найти сумму.
2. «Математический баскетбол».
Детям на двоих розданы по 1 карточке с нарисованными мячами. На «мячах» написаны числа. Задача учащихся назвать, суммой каких чисел является записанное на карточке число. Соседи не должны повторяться. Затем учитель просит назвать числа, разностью которых является записанное на «мяче» число. Те, кто правильно ответили – «забили мяч в кольцо». Если ученик ответил неправильно – он «передает мяч» другому ученику, который отвечает за него.
Изучение нового материала.
Для введения нового материала детям предлагается решить задачу.
- Сегодня мы научимся читать и решать выражение, содержащее скобки.
Вешаю на доску 7 картинок с мячами.
- Сколько мячей вы видите на доске? (7 мячей)
Два мяча убираю мальчику и один мяч – девочке.
- Что мы сделали с мячиками?
- Сколько мячиков отдали мальчику? (2)
- Сколько мячиков отдали девочке? (1)
- Сколько мячиков осталось? (4)
- Как мы получили число 4 из числа 7?
- Запишем выражение:
7 – 2 – 1
- Эту задачу можно решить другим способом.
- Сколько всего мячей отдали? (3)
- Как получили число 3? (к 1 прибавили 2)
- Что мы можем сделать, чтобы узнать, сколько мячей осталось? (из 7 вычесть 3)
- Какое мы действие сделали сначала? (сложение)
- Какое мы действие сделали затем? (вычитание)
- Чтобы записать этот пример используют скобки и записывают его так:
7 – (2 + 1)
- Скобки говорят, что первым выполняется действие в скобках.
- Ответ на выражение в скобках мы записываем над знаком действия.
- Как называется действие в скобках? (сложение)
- Как называется результат действия «сложение»?
- Значит, это выражение мы можем прочитать так: из 7 вычесть…? (сумму чисел 2 и 1)
Далее дети самостоятельно читают записанные в учебнике примеры, объясняют, чем они похожи, чем отличаются, какие знаки использованы в записи этих примеров, указывают, какое действие в каждом примере выполнялось первым.
В результате этой работы дети узнают назначение скобок
|
Поиск по сайту:
|
 с и в
с и в 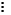 с) Þ (а + b): с = а: с + b: с
В начальной школе знакомство с данным свойством сводится к знакомству с правилом:
Чтобы сумму разделить на число можно на это число разделить каждое слагаемое и полученные результаты (частные) сложить.
Правило «Деление суммы на число» лежит в основе вычислительных приемов деления двузначного числа на однозначное.
Например: 48:4=(40+8):4=40:4+8:4=10+2=12
Рассуждение ученика: представляю число 48 в виде суммы разрядных слагаемых 40 и 8, нам удобно сначала каждое слагаемое разделить на 4 затем сложить полученные результаты, (частные) 10 и 2 и получить 12.
Деление разности на число
Для любых целых неотрицательных чисел а,b и натурального числа с верно равенство:
(а - b): с = а: с + b: с
("а,b ÎNo, с ÎN) (а
с) Þ (а + b): с = а: с + b: с
В начальной школе знакомство с данным свойством сводится к знакомству с правилом:
Чтобы сумму разделить на число можно на это число разделить каждое слагаемое и полученные результаты (частные) сложить.
Правило «Деление суммы на число» лежит в основе вычислительных приемов деления двузначного числа на однозначное.
Например: 48:4=(40+8):4=40:4+8:4=10+2=12
Рассуждение ученика: представляю число 48 в виде суммы разрядных слагаемых 40 и 8, нам удобно сначала каждое слагаемое разделить на 4 затем сложить полученные результаты, (частные) 10 и 2 и получить 12.
Деление разности на число
Для любых целых неотрицательных чисел а,b и натурального числа с верно равенство:
(а - b): с = а: с + b: с
("а,b ÎNo, с ÎN) (а 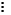 с и в
с и в 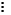 с) Þ (а - b): с = а: с - b: с
Данное свойство можно сформулировать в виде правила: Чтобы разность разделить на число можно на это число сначала разделить уменьшаемое, затем вычитаемое и из первого результата (частного) вычесть второй.
В начальной школе дети специально не знакомятся с данным правилом, но при выполнении некоторых заданий сталкиваются с его применением.
Например: сравни выражения (18-6):3 > 18:3-6. Выполняя это задание дети могут применить правило для выражения стоящего в левой части (18-6):3=18:3-6:3 и сравнив полученные выражения с выражениями стоящими в правой части, проанализировав отличия: 18:3-6 уменьшаемое 18:3, вычитаемое 6, следовательно, разность меньше и левая часть больше правой.
Деление произведения на число
Для любых целых неотрицательных чисел а,b и натурального числа с верно равенство: (а × b): с =(а: с) × b =(b: с) × а
(" а,b ÎNo, с ÎN) (а
с) Þ (а - b): с = а: с - b: с
Данное свойство можно сформулировать в виде правила: Чтобы разность разделить на число можно на это число сначала разделить уменьшаемое, затем вычитаемое и из первого результата (частного) вычесть второй.
В начальной школе дети специально не знакомятся с данным правилом, но при выполнении некоторых заданий сталкиваются с его применением.
Например: сравни выражения (18-6):3 > 18:3-6. Выполняя это задание дети могут применить правило для выражения стоящего в левой части (18-6):3=18:3-6:3 и сравнив полученные выражения с выражениями стоящими в правой части, проанализировав отличия: 18:3-6 уменьшаемое 18:3, вычитаемое 6, следовательно, разность меньше и левая часть больше правой.
Деление произведения на число
Для любых целых неотрицательных чисел а,b и натурального числа с верно равенство: (а × b): с =(а: с) × b =(b: с) × а
(" а,b ÎNo, с ÎN) (а 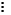 с) Þ (а × b): с =(а: с) × b
(" а,b ÎNo, с ÎN) (в
с) Þ (а × b): с =(а: с) × b
(" а,b ÎNo, с ÎN) (в 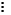 с) Þ (а × b): с =(b: с) × а
Данное свойство можно сформулировать в виде правила: Чтобы произведение разделить на число можно на это число разделить один из множителей и полученный результат (частное) умножить на второй множитель.
Деление числа на произведение
Для любых целых неотрицательных чисел а, b и натурального числа с верно равенство: а:(b × с) =(а: b): с =(а: с): b
(" а ÎNo, b, с ÎN) а:(b × с) =(а: b): с =(а: с): b
Данное свойство можно сформулировать в виде правила:
Чтобы число разделить на произведение можно это число разделить сначала на один из множителей и полученный результат (частное) разделить на другой множитель.
Эти правила лежат в основе вычислительных приемов деления чисел, оканчивающихся нулями.
Например: 480:6=(48·10):6=(48:6)·10=8·10=80 в основе решения лежит правило деления произведения на число.
II. Разработать фрагмент урока по ознакомлению учащихся с одним из свойств деления.
Повторить понятия суммы, частного, слагаемое, таблицу умножения.
Для знакомства с правилом деления суммы на число можно предложить детям задачу, имеющую два способа решения. Числа в условии подбирают так, чтобы все вычисления проходили в пределах таблицы умножения и соответствующих случаев деления.
Например: Двум мальчикам раздали 4 пирожных и по 6 конфет, так что у каждого получилось сладостей поровну. Сколько сладостей получил каждый?
1 способ. Сколько всего было сладостей? (4+6=10) Сколько сладостей получил каждый мальчик? (10:2=5) (равенство (4+6):2=5)
2 способ: Сколько пирожных получил каждый мальчик (4:2=2) Сколько конфет получил каждый мальчик? (6:2=3) Сколько сладостей всего получил каждый? (5) (равенство (4:2) + (6:2)=5)
Дети находят сходства (одинаковые числа, действия и ответы, различия (порядок выполнения действий). Вспомнив название выражения (1способ) записанного в скобках (4+6) и названия чисел при сложении (1 и 2 слагаемое) младшие школьники формулируют правило деление суммы на число
с) Þ (а × b): с =(b: с) × а
Данное свойство можно сформулировать в виде правила: Чтобы произведение разделить на число можно на это число разделить один из множителей и полученный результат (частное) умножить на второй множитель.
Деление числа на произведение
Для любых целых неотрицательных чисел а, b и натурального числа с верно равенство: а:(b × с) =(а: b): с =(а: с): b
(" а ÎNo, b, с ÎN) а:(b × с) =(а: b): с =(а: с): b
Данное свойство можно сформулировать в виде правила:
Чтобы число разделить на произведение можно это число разделить сначала на один из множителей и полученный результат (частное) разделить на другой множитель.
Эти правила лежат в основе вычислительных приемов деления чисел, оканчивающихся нулями.
Например: 480:6=(48·10):6=(48:6)·10=8·10=80 в основе решения лежит правило деления произведения на число.
II. Разработать фрагмент урока по ознакомлению учащихся с одним из свойств деления.
Повторить понятия суммы, частного, слагаемое, таблицу умножения.
Для знакомства с правилом деления суммы на число можно предложить детям задачу, имеющую два способа решения. Числа в условии подбирают так, чтобы все вычисления проходили в пределах таблицы умножения и соответствующих случаев деления.
Например: Двум мальчикам раздали 4 пирожных и по 6 конфет, так что у каждого получилось сладостей поровну. Сколько сладостей получил каждый?
1 способ. Сколько всего было сладостей? (4+6=10) Сколько сладостей получил каждый мальчик? (10:2=5) (равенство (4+6):2=5)
2 способ: Сколько пирожных получил каждый мальчик (4:2=2) Сколько конфет получил каждый мальчик? (6:2=3) Сколько сладостей всего получил каждый? (5) (равенство (4:2) + (6:2)=5)
Дети находят сходства (одинаковые числа, действия и ответы, различия (порядок выполнения действий). Вспомнив название выражения (1способ) записанного в скобках (4+6) и названия чисел при сложении (1 и 2 слагаемое) младшие школьники формулируют правило деление суммы на число
 1.Делимое 2916. Делитель 6
1.Делимое 2916. Делитель 6
 Высший разряд делимого — тысячи; две тысячи нельзя разделить на 6 равных частей так, чтобы в каждой части получилось хотя бы по одной тысяче. Раздробим 2 тысячи в сотни и прибавим 9 сотен, получим 29 сотен. Это число делится на 6 равных частей так, что в.каждой части получаются сотни. Значит, высший разряд частного — сотни. Сотни стоят на третьем месте справа, значит, в частном будут три цифры. Вместо трех цифр пока ставим три точки.
29 сотен разделим на 6, получим 4 сотни.
Узнаем, сколько всего сотен мы разделили. Для этого умножим 4 сотни на 6, получим 24 сотни.
Узнаем, сколько сотен осталось разделить. Для этого отнимем 24 сотни от 29 сотен, получим 5 сотен.
Остаток 5 сотен не делится на 6, следовательно, цифра частного подобрана правильно.
Раздробим 5 сотен в десятки, получим 50 десятков.
Прибавим 1 десяток, получим 51 десяток.
51 десяток разделим на 6, получим 8. И т. д.
Частное — 486. Важно, чтобы при делении ученики записывали каждую цифру в своей клетке. Аккуратные записи вообще, а при делении особенно сокращают число ошибок.
Высший разряд делимого — тысячи; две тысячи нельзя разделить на 6 равных частей так, чтобы в каждой части получилось хотя бы по одной тысяче. Раздробим 2 тысячи в сотни и прибавим 9 сотен, получим 29 сотен. Это число делится на 6 равных частей так, что в.каждой части получаются сотни. Значит, высший разряд частного — сотни. Сотни стоят на третьем месте справа, значит, в частном будут три цифры. Вместо трех цифр пока ставим три точки.
29 сотен разделим на 6, получим 4 сотни.
Узнаем, сколько всего сотен мы разделили. Для этого умножим 4 сотни на 6, получим 24 сотни.
Узнаем, сколько сотен осталось разделить. Для этого отнимем 24 сотни от 29 сотен, получим 5 сотен.
Остаток 5 сотен не делится на 6, следовательно, цифра частного подобрана правильно.
Раздробим 5 сотен в десятки, получим 50 десятков.
Прибавим 1 десяток, получим 51 десяток.
51 десяток разделим на 6, получим 8. И т. д.
Частное — 486. Важно, чтобы при делении ученики записывали каждую цифру в своей клетке. Аккуратные записи вообще, а при делении особенно сокращают число ошибок.
 Создалась проблемная ситуация.
- Можно ли выполнить это задание? (Нет.) - В чем затруднение? (Использовались разные мерки. яблоки и бананы) Для выхода из проблемной ситуации учитель задает вопрос:- Что нужно сделать, чтобы это задание можно было выполнить?(Использовать одинаковую мерку.)- Существует единая мерка для нахождения массы. Кто из вас знает, как эта мерка называется? (Килограмм.)Учитель показывает гирю – 1 килограмм.
- Можем мы теперь выполнить задание? Учащиеся находят массу дыни, массу пакета риса и сравнивают
их.
Создалась проблемная ситуация.
- Можно ли выполнить это задание? (Нет.) - В чем затруднение? (Использовались разные мерки. яблоки и бананы) Для выхода из проблемной ситуации учитель задает вопрос:- Что нужно сделать, чтобы это задание можно было выполнить?(Использовать одинаковую мерку.)- Существует единая мерка для нахождения массы. Кто из вас знает, как эта мерка называется? (Килограмм.)Учитель показывает гирю – 1 килограмм.
- Можем мы теперь выполнить задание? Учащиеся находят массу дыни, массу пакета риса и сравнивают
их.
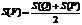

 - называются числовыми выражениями. Т.об. ч.в. содержит числа и знаки математических действий.
В нач. шк. ч.в. содержат действия +, -, ·,:. Ч.в. может содержать одно или несколько действий, а также (), определяющие порядок выполнения этих действий, напр. (5+3)·4. Если выполнить все действия в указанном порядке, то в результате получается число, к-ое называется значением ч.в., напр. (2+3)·1= 5.
Название ч.в. определяется последним действием, напр. (3 + 5)·2; 3+5 · 2. При чтении ч.в. используются названия компонентов и название действий, напр. (2+3).
При нахождении значения выражений применяется правило порядка выполнения действий:
1.Если выражение содержит только действия сложение и вычитание или только действия умножение и деление, то действия в выражении могут выполняться по порядку.
2.Если выражение содержит одновременно действия сложения или вычитания, а также действия умножение или деление, то сначала выполняются действия умножение и деление по порядку, а затем сложение и вычитание по порядку.
3.Если выражение содержит скобки, то сначала выполняются действия в скобках с учетом правил 1 и 2, а потом все остальные действия с учетом этих же правил.
Разработать фрагмент урока по ознакомлению учащихся с порядком выполнения арифметических действий.
Порядок выполнения арифметических действий в выражении — это последовательность проводимых вычислений в данном выражении.
Правила о порядке выполнения арифметических действий вводятся постепенно, начиная с 1 класса, когда дети имеют дело с выражениями, содержащими только сложение и вычитание. Здесь они усваивают, что действия выполняются в том порядке, как они записаны: слева направо. Во 2 классе вводятся скобки как знаки, указывающие на изменение порядка выполнения действий. Правила о порядке выполнения действий усложняются при ознакомлении с умножением и делением в теме «Числа от 1 до 100». В дальнейшем, на последнем году обучения в начальной школе, рассматриваются новые для учащихся правила о порядке выполнения действий в выражениях, содержащих две пары скобок или два действия внутри скобок. Эти правила иллюстрируются довольно сложными примерами, содержащими сначала 2—3, а затем 3—4 арифметических действия.
В результате дети должны освоить следующее правила:
- называются числовыми выражениями. Т.об. ч.в. содержит числа и знаки математических действий.
В нач. шк. ч.в. содержат действия +, -, ·,:. Ч.в. может содержать одно или несколько действий, а также (), определяющие порядок выполнения этих действий, напр. (5+3)·4. Если выполнить все действия в указанном порядке, то в результате получается число, к-ое называется значением ч.в., напр. (2+3)·1= 5.
Название ч.в. определяется последним действием, напр. (3 + 5)·2; 3+5 · 2. При чтении ч.в. используются названия компонентов и название действий, напр. (2+3).
При нахождении значения выражений применяется правило порядка выполнения действий:
1.Если выражение содержит только действия сложение и вычитание или только действия умножение и деление, то действия в выражении могут выполняться по порядку.
2.Если выражение содержит одновременно действия сложения или вычитания, а также действия умножение или деление, то сначала выполняются действия умножение и деление по порядку, а затем сложение и вычитание по порядку.
3.Если выражение содержит скобки, то сначала выполняются действия в скобках с учетом правил 1 и 2, а потом все остальные действия с учетом этих же правил.
Разработать фрагмент урока по ознакомлению учащихся с порядком выполнения арифметических действий.
Порядок выполнения арифметических действий в выражении — это последовательность проводимых вычислений в данном выражении.
Правила о порядке выполнения арифметических действий вводятся постепенно, начиная с 1 класса, когда дети имеют дело с выражениями, содержащими только сложение и вычитание. Здесь они усваивают, что действия выполняются в том порядке, как они записаны: слева направо. Во 2 классе вводятся скобки как знаки, указывающие на изменение порядка выполнения действий. Правила о порядке выполнения действий усложняются при ознакомлении с умножением и делением в теме «Числа от 1 до 100». В дальнейшем, на последнем году обучения в начальной школе, рассматриваются новые для учащихся правила о порядке выполнения действий в выражениях, содержащих две пары скобок или два действия внутри скобок. Эти правила иллюстрируются довольно сложными примерами, содержащими сначала 2—3, а затем 3—4 арифметических действия.
В результате дети должны освоить следующее правила: