Мат. модель ЗЦЛП имеет вид:
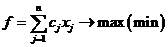
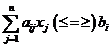
, где Z – множество целых чисел
Разложенные задачи полностью целочисленные, в которых условие целочисленности распространяются на все переменные и частично целочисленны, в целочисленности налагается только на часть переменных.
Если в (2) среди 
и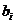 
есть дробные числа, то каждое уравнение или неравенство с дробными коэффициентами может привести к общему знаменателю и затем обе части умножить на этот общий знаменатель, поэтому не нарушив общности рассуждений, можно предполагать, что коэффициенты целочислены.
Решение целочисленных и непрерывных задач оптимизации имеет принципиальные различия, суть которого заключается в следующем: непрерывные задачи обычно решаются симплекс-методом с построением симплекс-таблиц.
Известно, что для ЗЛП экстремум достигается в крайней точке выпуклого множества или в точке, в которой является выпуклой линейной комбинацией крайних точек. Для ЗЦЛП точкой оптимума может быть любая точка области допустимых решений, поэтому невозможно заменить дискретную задачу непрерывным аналогом, и найдя соответствующее решение и округлить его значение до ближайших целых значений.
Пусть целая часть числа x – [x], огромная – {x}, тогда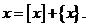 
Если даже оптимальный непрерывной задачи, округлённой до целых значений компонент окажется допустимым, то целевая функция может вести себя так, что её значение будет на нём значительно хуже, чем на оптимальном плане целочисленной задачи.
Перечисленные проблемы предопределяли необходимость разработки специальных методов решения ЗЦЛП, ибо методы последовательного улучшения приводит к целочисленному решению лишь для немногих задач. Методы ЦЛП можно разделить на 3 основные группы:
1. Метод отсечения.
2. Комбинаторные.
3. Приближённые
Сущность 1 состоит в том, что сначала задача решается без условия целочисленности. Если полученный план будет целочисленным, то задача решена. Решение обладает следующими свойствами:
1) Оно должно быть линейным.
2) Должно отсекать найденный оптимальный нецелочисленный план.
3) Не должно отсекать ни одного целочисленного плана.
Дополнительные ограничения, обладающие указанными свойствами, называются правильным отсечением. Затем полученные оптимизационные задачи решаются с учётом нового ограничения. После этого в случае необходимости добавляется новое ограничение.
Геометрическое добавление каждого линейного ограничения отвечает проведению плоскости (гиперплоскости), которая отсекает от многоугольника (многогранника) некоторую его часть вместе с оптимальной точкой с нецелевыми координатами, но не затрагивая ни одной из целочисленных точек этого многоугольника.
Метод Гомори.
Основная идея метода отсекающих плоскостей состоит в том, что на каждом шаге рассматривается задача с ослабленными ограничениями без требования целочисленности, для которой по специальному алгоритму строится некоторое дополнительное ограничение, отсекающее только некоторые нецелочисленные точки. Если полученный в результате оптимальный план содержит только целые компоненты, то автоматически получается соответст. решению ЗЦЛП. В противном случае к системе ограничений задачи должно быть добавлено такое ограничение, для которого:
1) Найденный нецелочисленный оптимальный план не удовлетворяет вновь добавленному ограничению;
2) Любой допустимый целочисленный план непрерывной задачи 1-4 удовлетворяет вновь добавленному ограничению.
Приведём обобщённую схему алгоритма Гомори. Структурно он делится на, т. н., большие итерации, каждая из которых содержит этапы:
1. Решение текущей задачи 1, 2 отбросит условия неотрицательности 3 симплекс-методом (малая итерация). Пусть решение исходной задачи с ослабленными ограничениями дало на последнем шаге, соответствующему оптимальному решению, следующие выражения, основных переменных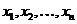 
через свободные переменные 
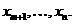Кратко это записывается в виде:
Как следует из теории симплекс-метода оптимальным решением задачи в этом случае является вектор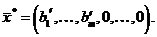 
2. Если все компоненты оптимального плана, полученного на первой итерации в целом, то он является оптимальным и для ЗЦЛП 1-4. Если задача ЛП 1-3 не разрешима, то и ЗЦЛП 1-4 также не разрешима. Если среди компонентов оптимального плана есть не целая, то перейдём к следующему этапу.
3. Среди базисных нецелых компонентов оптимального плана следует выбрать компоненту с наибольшей дробной частью.
Пусть компонента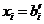 
не целое число. Рассмотрим уравнение, в котором 
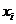базисная переменная:
, где R – множество индексов свободных переменных.
Разобьем все коэффициенты и свободные члены уравнения (5) на 2 слагаемых: целую и дробную часть.
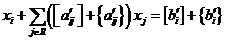
или
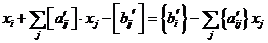
Для любого целочисленного решения задачи левая часть (6) – есть целое число, следовательно и правая часть равенства также будет целое число, причём правая часть равенства (6) должна удовлетворяет неравенству:
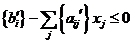
Это будет сечение Гомори. Т. о., третья итерация состоит в построении для нецелевой базисной компоненты условия отсечения.
4. Неравенство (7) выделением дополнительной неотрицательной целочисленной переменной преобразуется в уравнение и присоединяется к ранее решённой задаче (включить его в симплекс-таблицу с нецелочисленным оптимальным планом). Формируется новая текущая задача. Переход на начало следующей большой итерации.
5. Полученная расширенная ЗЛП решается симплекс-методом. Если полученный оптимальный план будет целочисленным, то ЗЦЛП 1-4 решена. В противном случае следует вернуться к пункту алгоритма 3. Если задача разрешима в целых числах, то после конечного числа итерации оптимальный целочисленный план будет найден.
Замечание:
· Если в процессе решения появится строка с нецелым свободным членом и целыми остальными коэффициентами, то соответствующее уравнение не имеет решения в целых числах. В таком случае и данная задача не имеет целочисленного оптимального плана.
· Если число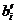 
с наибольшей дробной частью окажется несколько то из них выбирается 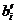первое по коэффициенту.
· Несмотря на точность, методы отсечения имеют весьма ограниченную применимость, с их помощью нельзя решить задачи большой размерности.
· При практической реализации метода Гомори на ЭВМ следует считаться с ошибками округления.
8. Пример решения ЗЦЛП методом Гомори.
Находим общее решение системы:
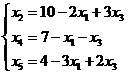
Выразим целевую функцию через свободные переменные x1 и x3:
Полученный стандартный вид ЦФ применим для решения задач симплекс-методом.
Итерация 1. Используя обычный симплекс-алгоритм решаем непрерывный аналог исходной задачи в котором игнорируются условия целочисленности.
| X1 | X2 | X3 | X4 | X5 | Bi | |
| X2 | -3 | |||||
| X4 | ||||||
| X5 | -2 | |||||
| f | -3 | -3 |
| X1 | X2 | X3 | X4 | X5 | Bi | |
| X2 | -5/3 | -2/3 | 22/3 | |||
| X4 | 5/3 | -1/3 | 17/3 | |||
| X1 | -2/3 | 1/3 | 4/3 | |||
| f |
| X1 | X2 | X3 | X4 | X5 | Bi | |
| X2 | -1 | |||||
| X3 | 3/5 | -1/5 | 17/5 | |||
| X1 | 2/5 | 1/5 | 18/5 | |||
| f | 3/5 | 4/5 | 22/5 |
Как видно из последней симплекс-таблицы полученный план: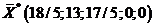 
является оптимальным, при котором ЦФ 
.
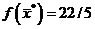Однако этот план не является целочисленным, т. к. 
и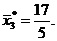 
Выбираем из чисел с дробной частью
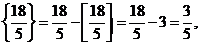
Выбираем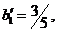 
базисная переменная x1. Из последней симплексной таблицы выписываем строку с базисной переменной 
Тогда с учётом (7) сечение запишется в виде:
или 
где x6 – дополнительная неотрицательная переменная.
Присоединяя полученное ограничение к 1 задаче, получим другую задачу, после чего переходим к следующей «большой» итерации.
Итерация 2. Исходная симплекс-таблица для поставленной задачи получается путём добавления к симплекс-таблице 3 первой задачи строки соответст. введённому сечению.
| X1 | X2 | X3 | X4 | X5 | X6 | bi | |
| X2 | -1 | ||||||
| X3 | 3/5 | -1/5 | 17/5 | ||||
| X1 | 2/5 | 1/5 | 18/5 | ||||
| X6 | -2/5 | -1/5 | -3/5 | ||||
| f | 3/5 | 4/5 | 22/5 |
Решение: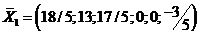 
является условно-оптимальным, поскольку условие оптимальности в последней строке таблицы 4 выполнено, но в столбце свободных членов есть отрицательный элемент.
Несмотря на это продолжаем выполнять симплексную операцию, выбирая разрешающую строку и разрешающий столбец по положительной основе.
Цель этой итерации: не увеличивать значение ЦФ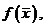 
как в симплекс-методе, а получить опорное решение новой задачи, выводя из базиса переменную x6, т. к. 
в базис вместо x0 введём переменную x4, получим следующую симплекс-таблицу:
| X1 | X2 | X3 | X4 | X5 | X6 | bi | |
| X2 | -3/2 | 5/2 | 23/2 | ||||
| X3 | -1/2 | 3/2 | 5/2 | ||||
| X1 | |||||||
| X4 | -1/2 | -5/2 | 3/2 | ||||
| f | 1/2 | 3/2 | 7/2 |
Полученный план является целочисленным. Выбираем из чисел 23/2; 5/2; 3/2 число с наибольшей дробной частью. У всех у них дробная часть равняется ½.
Выбираем 1 строку:
Используя формулу (7) строим сечение:
Добавим 2-е сечение к таблице 5, получаем таблицу 6.
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | bi | |
| X2 | -3/2 | 5/2 | 23/2 | |||||
| X3 | -1/2 | 3/2 | 5/2 | |||||
| X1 | ||||||||
| X4 | 1/2 | -5/2 | 3/2 | |||||
| X7 | -1/2 | -1/2 | -1/2 | |||||
| F | 1/2 | 3/2 | 7/2 |
План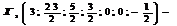 
базисное решение новой задачи, но не опорное. Введём в базис переменную x5 вместо x7, т. к.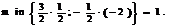 
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | bi | |
| X2 | -13 | |||||||
| X3 | -1 | |||||||
| X1 | ||||||||
| X4 | -3 | |||||||
| X5 | -2 | |||||||
| F |
Получим целочисленное решение 3 задачи, оно будет оптимально и для исходной задачи, т. е.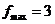 
при 
9. Сущность метода отсечений - один из методов ЦЛП
Сущность методов отсечения состоит в том, что сначала задача решается без условия целочисленности. Если полученный план будет целочисленным, то задача решена, в противном случае к ограничению задачи добавится новое ограничение, обладающее следующими свойствами:
1) оно должно быть линейным,
2) должно отсекать найденный нецелочисленный план,
3) не должно отсекать ни одного целочисленного плана.
Дополнительные ограничения, обладающие указанными свойствами, называются правильным отсечением. Затем полученные оптимизационные задачи решают с учетом нового ограничения. После этого в случае необходимости добавляется еще одно ограничение и т.д. Геометрически добавление каждого линейного ограничения отвечает проведению плоскости (гиперплоскости), которая отсекает от многоугольника (многогранника) некоторую его часть вместе с оптимальной точкой с нецелочисленной координацией, но не затрагивает ни одной из целочисленных точек этого многоугольника.
Данный метод впервые был предложен Р.Е. Гомори в 1957-1958гг.,который также носит название метода отсекающих плоскостей, предназначен для ЗЛП в канонической форме 1-4. Т.о., основная идея метода состоит в том, что на каждом шаге рассматривается задача с ослабленными ограничениями без требования целочисленности, для которой по специальному алгоритму строится некоторое дополнительное линейное ограничение (отсечение), отсекающее только некоторые нецелочисленные точки. Он существенно использует известную симплексную процедуру. Отправной точкой для решения задачи 1-4 является решение ее непрерывного аналога, т.е. ЗЛП без учета целочисленности. Если получаемый в результате оптимальный план содержит только целые компоненты, то автоматически получается ЗЦЛП. В противном случае в системе ограничений задачи д/б добавлено такое ограничение, для которого:
1)найденный нецелочисленный оптимальный план не удовлетворяет вновь добавляемому ограничению,
2)любой допустимый целочисленный план задачи 1-4 удовлетворяет вновь добавляемому ограничению
Основные понятия теории игр.
Игрой называется математическая модель конфликтной ситуации.Стороны, участвующие в конфликте называются участниками игры или игроками, а исход конфликта-выигрыш.В систему условий, регламентирующих возможные варианты действия сторон, объем информации каждой стороны о поведении другой, а также результат, к которому приводит данная совокупность действий составляет правила игры. Игра состоит из ходов. Причем под ходом понимается выбор одного из предусмотренных правилами игры действий. Ходы бывают личные и случайные. Решение, принятое игроком при личном ходе называется выбранным ходом. Случайным ходом называется выбор и осуществление одного из предписанных правилами игры действия, которое производится не самим игроком, а некоторым механизмом случайного выбора. Для каждого случайного хода аправила игры определяют распределение ероятностей возможных исходов. Возможное для игрока действие называют стратегией. Стратегия называется оптимальной, если она при многократном повторении игры обеспечивает игроку максимальную возможность среднего выигрыша. Заинтересованность игроков в ситуации проявляется в том, что каждому игроку I в каждой ситуации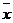 
приписывается число, выражающее степень удовлетворения его интересов в этой ситуации. Это число называется выигрышом игрока I в ситуации 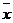и обозначается через H(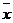). Если число стратегий у каждого игрока конечно, то игра называется крнечной. Если у игрока А m-стратегии, а у игрока В n-стратегии, то игра называется игрой M×N. В общем виде постановка задачи теории игр производится следующим образом. Имеется некоторая операция,в которой участвуют 2 игрока А и В с противоположными интересами. Имеются правила, регламентирующие результаты, к которым приводят возможные варианты действий игроков. Результаты действий выражены в количественной форме и обозначены (математическое ожидание выигрыша игрока А, сделавшего свой i-ый ход при j-ом ходе игрока В. Тогда целью теории игр является выработка оптимальных для игроков стратегий, которые при многократном повторении игры обеспечивают максимально возможный выигрыш и минимально возможный средний проигрыш. Рассмотрим конечную игру m×n, в которой игрок А имеет m-стратегию (а1,а2,...аn), а игрок В n-стратегию(b1,b2, …bn). Если игроки используют только личные ходы, то выбор стратегии А и В однозначно определяет , т.е. число, характеризующее выигрыш игрока А при проигрыше игрока В. Причем может быть и положительным и отрицательным. Будем считать, что при ≥0 игрок аА выигрывает, а игрок В проигрывает величину .Если < 0, то выигрывает игрок В и проигрывает игрок А. В этом случае вместо проигрыша говорят об отрицательном выигрыше игрока А. Если в игре используют случайные ходы, то выигрыш при 2 стратегии ai и aj является случайным. В этом случае за оценку ожидания выирыша берется его мат.ожидание. Предположим, что нам известны все значения в игре m×n. Эти значения запишем в виде таблицы, называемой платежной матрицей. Строки матрицы соответствуют стратегии ai, а столбцы – стратегии aj.
Построение платежной матрицы не всегда просто, поскольку количество стратегий m,n могут оказаться очень большими. Однако любая конечная игра может быть приведена к матричному виду.
Игры с нулевой суммой относят к классу антогонистических игр.
Среди всех чисел ai выберем наибольшее: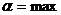 
{ 
}. Число а называется нижней ценой игры. Это гарантированный выигрыш игрока А при любой стратегии игрока В.
Среди всех чисел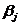 
выберем наименьшее. Это гарантированный проигрыш игрока В.
Фактический выигрыш игрока А при разумных действиях партнеров ограничен нижней и верхней ценой игры. Если верхняя и нижняя цены игры совпадают, то общее значение верхней и нижней цены игры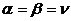 
называется ценой игры. В эом случае игра называется вполне определенной или игрой с Седловой точкой. Седловой точкой называется элемент платежной матрицы, одновременно мин в своей строке и макс в своем столбце. Седловой точке соответствуют оптимальные стратегии игроков Ai и Bj, их совокупность – это решение игры, которое обладает следующим свойством: если один из игроков придерживается своей оптимальной стратегии, то для другого отклонение от его оптимальной стратегии невыгодно. В этом случае говорят, что игра имеет решение в чистых стратегиях.