Марковские процессы с дискретным состоянием в дискретном времени.

Вероятности состояний Pk(t) Марковского случайного процесса – вероятности того,что случайный процесс в в момент времени t нач-ся в сост-ии Sк: P(k)*P{x(t)=Sk}

Переходные вероятности марковского процесса – это вероятности перехода процесса (системы) из одного состояния в любое другое: Pij(∆t)=P{x(x+∆t)=SjIx(t)Si}

Марковский процесс однородный, если вер-ти перехода за 1 времени не зависят от того, где на осн времени происходит переход. Наиболее простым процессом яв-ся цепь Маркова – Марковский случайный процесс с дискретным временем и дискретном конечном состоянии.

При анализе цепи Маркова сост-т граф сост-ий, на к-ом отмечают все состояния цепи и не нулевые вероятноси перехода за 1 шаг. Марковскую цепь можно представить себе так, как будто точка, изображающая систему, случайным образом перемещается по графу сост-ий, поскакивая за 1 шаг из состояние в состояние или задерживаясь на них шагов в одгом и том же состоянии. Переходные вероятности цепи Маркова за 1 шаг Pij записывают в виде матрицы: P = II Pij II – матрица вероятности перехода.

Рпименение m→∞ в системе уст-ся некоторый предв-ый стационарный режим, к-ый сост-т в том, что система слчайным образом меняет свои состояния, но вероятность каждого из них уже не зависит от времени, каждое из состояний осущ-ся с некот-ой вероятностью среди временного пребывания в сост-ие Si за время T=PiT, где Pi – пред-ая вероятность состояния Si, Переходные матрицы обладают свойством: все элементы их неотрицательны, их сумм по строкам равны 1. Матрицы с таким свойством называют стохастическими. Матричный переход позволяет вычислить вероятность любой траектории цепи Маркова с помощью теории умножения вероятностей.

Для однородных цепей Маркова матричный переход не зависит от времени. При изучении цепей Маркова наибольший интерес представляет: вероятности перехода за m шагов, распределение по составу m→бесконечности, средне время пребывания в определенном состоянии. Рассмотрим однородную цепь Маркова с n состоянием. Для получения вероятности перехода из состояния Si в Sj за m шагов в соответствии с формулой полной вероятности следует просуммировать произведение вероятностей перехода из состояния Si в промежуточное состояние Sk за l шагов на вероятность перехода из Sk в Sj за оставшиеся m-l шагов.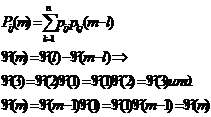

Возникает вопрос: что будет происходить с системой при m→беск. Будут ли p1(m)…pn(m) стремится к каким-то пределам? Эти пределы, если они существуют называются предельными вероятностями состояний. Вектор р, состоящий из предельных вероятностей должен удовлетворять соотношению:

среднее время возвращения в сост-ие Si=1/Pi.

17 Раннее была рассмотрена Марковская цепь, т.е случайн. процесс, протекающий в системе, ктр. случ. образом может переходить из сост-я в сост-е только в некоторые заранее опред-ые моменты времени. На практике значит-о чаще встреч. ситуации, когда переходы системы из сост-я в сост-е происходят не фиксированные, а в произвол. моменты времени.

Например: выход из строя любого элемента аппаратуры, окончание ремонта этого элемента и т.д. Для описания таких процессов м.б. применена схема марковск. случ. процесса с дискретн. Состояниями и непрерывн. временем. Для вер-ти сост-ий Pi(t) такого процесса выполнены. Сумма Рi(t)=1

В случае процесса с непрерывн. временем, вер-ть перехода системы из сост-я в сост-е в точный момент времени t=0, также как вер-ть любого отдельн. знач-я непрерывн. случ. величины. Поэтому вместо переходных вер-ей Pij рассм-ют плотности вер-ей перехода(ПВП). ПВП Лi- это предел отнош-я вер-ей перехода системы за время дельта t из сост-я Si в Sj к длине промежутка дельта t, когда дельта t стрем-ся к 0.

Лij=lim Pij(дельта t)/дельта t. Плотность вер-ти перехода опред-ся для i не равное j.

Для однородн. Марковского процесса Лij не зависит от t; при построении графов сост-ий Марк. процесса, над стрелками м/у сост-ми указывают плотность вер-ей перехода. Этот граф назыв. размеченным графом сост-ий. Зная его, можно опред-ть вероятностные сост-я p1(t), p2(t)...pn(t)/ Они составят цифровые ур-я, позвол-ие опред-ть p1(t), p2(t)...pn(t). Выведем эти ур-я, исходя из конкретн. примера. Пусть система имеет 3 возм. сост-я S1, S2, S3. Причем возможны переходы из S1 в S2, из S2 в S3, из S3 в S1 или S2.

dp1/dt=-Л12p1+Л31p3

dp2/dt=-Л23p2+Л12p1+Л32p3

dp3/dt=-Л32p3-Л31p3+Л23p2

Интегриров-е этой системы дает искомую вер-ть сост-ий как функцию времени. Нужны начальные усл-я. Например, если при t=0 система находится в сост-ии S1 то p1(0)=1, p2(0)=0, p3(0)=0. В левой части каждого ур-я стоит производная вер-ти сост-я, а правая часть содержит столько членов, сколько стрелок связ-о с данным сост-ем. Если стрелка напр-на из сост-я, соотв-ий член имеет знак -. Если в состояние- знак +. Каждый член равен произвед-ю плотности вер-ти перехода, соотв. данной стрелке, умнож-ой на вер-ть того сост-я, из ктр. исходит стрелка.

18 Происхождение термина «процесс гибели и размножения» идет в начало биол. задач, где подобной схемой описыв-ся процесс изм-я числ-ти популяции. Пример графа сост-ий имеет вид:

Пример: Технич. устройство сост. Из 3-х одинак. узлов. Каждый из них может выходить из строя(отказывать). Отказавший узел немдл-о начинает восстан-ся. Состояние системы пронумеруем по числу неисправных узлов. S0-все узлы исправны, S1-один узел отказал, 2 исправны, S2- два узла отказали, 1 работает, S3- все 3 узла отказали. Граф сост-ий имеет вид: 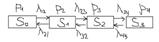По графу сост-ий запишем дифференц. ур-е Колмогорова: (система):

dp1/dt=-Л12p1+Л21p2

dp1/dt=-(Л23+Л21)+Л12p1+Л32p3

dpn-1/dt=-(Лn-1,n-2+Лn-1,n)pn-1+Лn-2,n-1 pn-2+Лn,n-1 pn

dp1/dt=-Лn,n-1 pn+Лn-1,n pn-1

В общем виде решить такую систему сложно, но можно найти предельн. вер-ти сост-ий. Для этого надо положить все левые части в производные(равные 0). Система дифферен. ур-ий превратится в СЛАУ. Совместно с усл-ем сумма pi=1. Эти ур-я дают возм-ть вычичлить p1, p2...pn Эти ур-я выглядят так: (система):

Л12p1=Л21p2

Л23p2=Л32p3

………………………..

Лn-1 pn-1=Лn,n-1 pn

P1+p2+...pn=1

Решая ее, найдем:

p2=Л12/Л21 p1

p3=Л23/Л32 p2=Л23*Л12/Л32*Л21 p1

p1=Л12/Л21 p1+Л23*Л12/Л32*Л21 p1+...+Лn-1,n Лn-2,n-1...Л12/Лn,n-1 Лn-1,n-2.. p1=1

Очевидно, что из последн. ур-я мы можем найти p1, а затем p2, p3...

p1=1/1+ Л12/Л21+ Л23*Л12/Л32*Л21+...+ Лn-1, Лn-2,n-1...Л12/Лn,n-1 Лn-1,n-2.. Л21

Прибор состоит из 3 узлов, поток отказов простейший, средн. Время безо тказной работы каждого узла =средн. tб. Отказавший узел сразу начинает ремонтироваться. Средн. время ремонта(восстан-е узла) =средн. tр Законы распред-я этого времени показательны(поток восстан-я простейший). Найти средн. производит-ть приборов, если при 3-х работающих узлах она 100%, при 2-х-50%, а при 1-ом и менее прибор вообще не работает.

Решение: состояние системы нумеруют по числу неисправных узлов; S0-все 3 узла исправны, S1-один узел отказал и восстан-ся, 2 неисправны; S2-2 узла восстан-ся, 1 исправен; S3-все 3 узла восстан-ся.

По стрелкам вправо систему переводят отказы. Если система находится в состоянии S0, то работают 3 узла, каждый из них подвергается потоку отказов с интенс-ю 1/tб(среднее). Значит поток отказов, действующий на всю систему в 3 раза интенсивнее. Л01=3/tб(среднее) Если система наход-ся в сост. S1, то раб-ют 2 узла. Общий поток отказов имеет интенсив-ть 2/tб(среднее); Л23=1/tб(средн.) По стрелкам влево систему переводят ремонты(восстан-е). Средн. время восстан-я узла =tр(средн). Значит интенс-ть потока восстан-ий, действ-го на восстан-ый узел =М=1/tр(средн), на 2 узла =2/tр(средн.), на 3 узла =3/tр(средн). Эти значения Л10, Л21, Л32 и проставл-ы стрелок, ведущих влево в графе сост-ий системы. Решение системы:

p0=1/1+3(tр/tб)+3(tр/tб)^2+(tр/tб)^3

p1=3(tр/tб)p0

p2=3(tр/tб)^2p0

p3=(tр/tб)^3po

Зададим конкретн. знач-ми tб=10 часов, tр=5 часов, откуда p0=8/27, p1=12/27, p2=6/27, p3=1/27. Средняя производ-ть прибора в восстан. режиме: 100%p0+50%p1=(8/27+1/2*12/27)*100%=51,9% номинала.

Вопрос 19. Модель В. Леонтьева. межотраслевого баланса.

Цель балансового анализа – ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из n отраслей, чтобы удовлетворить все потребности в продукции этой отрасли? При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции, а с другой – как потребитель продукции и своей, и произведенной другими отраслями.

Связь между отраслями, как правило, отражается в таблицах межотраслевого баланса, а математическая модель, позволяющая их анализировать, разработана в 1936 г. американским экономистом В. Леонтьевым.

Рассмотрим n отраслей, каждая из которых производит один агрегированный продукт. Объемы валовой продукции отраслей обозначим x1,x2,...,xn. Вся продукция xi i-ой отрасли (i = 1,2,...,n) делится на промежуточную zi и конечную yi. Промежуточная продукция расходуется в процессе производства, а конечная поступает в сферу конечного потребления.

Обозначим xij – объем продукции i-ой отрасли, используемой за отчетный период в процессе производства в j-ой отрасли.

Система балансовых уравнений имеет вид:

x1=z1+y1=x12+x13+...x1n+y1

x2=z2+y2=x21+x22+...x2n+y2 (1)

................................................

xn = zn+yn=xn1+xn2+...xnn+yn

 

Обозначим отношение xij/xj = aij. Параметры aij называются коэффициентами прямых затрат. Они показывают, какое количество продукции i – ой отрасли необходимо истратить на текущее производственное потребление в j-ой отрасли при выпуске ею единицы продукции.

Введем обозначения:

x1 y1 a11 a12... a1n

x = x2; y = y2; A = a21 a22... a2n

...............................

xn yn an1 an2... ann

 

Систему балансовых уравнений (1) можно преобразовать и записать в матричной форме в виде:

X = AX + Y (2) или

X = (E-A)¯¹Y (3)

Здесь E – единичная матрица. Матрица C = (E-A)¯¹ называется матрицей коэффициентов полных затрат.

Баланс продукции на основе коэффициентов прямых затрат дает возможность определить объемы валовой продукции, которые бы обеспечили получение конечной продукции отраслей в заданных объемах.

Вопрос 20. Применение функций в экономике.

Функции находят широкое применение в экономической тео­рии и практике. Спектр исполь­зуемых в экономике функций весьма широк: от простейших линейных до функций, получае­мых по определенному алгоритму с помощью так называемых рекуррентных соотношений, связывающих состояния изучаемых объектов в разные периоды времени.

Наряду с линейными, используются нелинейные функции, такие, как дробно - рациональные, степенные (квадратная, куби­ческая и т.д.), показательные (экспоненциальные), логарифмиче­ские и другие функции. Периодичность, колеблемость ряда эко­номических процессов позволяет также использовать тригоно­метрические функции.

Наиболее часто используются в экономике следующие функ­ции:

1. Функция полезности (функция предпочтений) - в широком смысле зависимость полезности, т.е. результата, эффекта некоторого действия от уровня (интенсивности) этого действия.

2. Производственная функция - зависимость результата про­изводственной деятельности от обусловивших его факторов.

3. Функция выпуска (частный вид производственной функции) - зависимость объема производства от наличия или потребления ресурсов.

4. Функция издержек (частный вид производственной функции) - зависимость издержек производства от объема продукции.

5. Функции спроса, потребления и предложения - зависимость объема спроса, потребления или предложения на отдельные товары или услуги от различных факторов (например, цены, дохода и т.п.).

Учитывая, что экономические явления и процессы обуслов­ливаются действием различных факторов, для их исследований широко используются функции нескольких переменных. Среди этих функций выделяются мультипликативные функции, позволяю­щие представить зависимую переменную в виде произведения факторных переменных, обращающего его в нуль при отсутствии действия хотя бы одного фактора.

Используются также сепарабельные функции, которые дают возможность выделить влияние различных факторных перемен­ных на зависимую переменную, и в частности, аддитивные функ­ции, представляющие одну и ту же зависимую переменную как при суммарном, но раздельном воздействии нескольких факто­ров, так и при одновременном их воздействии.

Если действием побочных факторов можно пренебречь или удается зафиксировать эти факторы на определенных уровнях, то влияние одного главного фактора изучается с помощью функции одной переменной. Приведем примеры:

1. Исследуя зависимости спроса на различные товары от дохода

y = b₁(x-a₁) (x> a₁) y = b₂(x-a₂) (x> a₂) y = b₃x(x-a₃) (x> a₃)

x-c₁ x-c₂ x-c₃

(функции Л.Торнквиста), мы можем установить уровни доходов a₁ – товары первой необходимости, a₂ - товары второй необходимости, a₃ – предметы роскоши при которых начинается приобретение тех или иных товаров и уровни (точки) насыщения b₁, b₂ для групп товаров первой и второй необходимости (рис. 5.22).

 

2. Рассматривая в одной системе координат кривые спроса и пред­ложения, можно установить равновесную (рыночную) цену данного товара в процессе формирования цен в условиях конкурентного рынка (паутинообразная модель) (рис. 5.23).

3. Изучая в теории потребительского спроса кривые безразличия (линии, вдоль которых полезность двух благ х и у одна и та же), напри­мер, задаваемые в виде ху = U, и линию бюджетного ограничения р_xx + р_yу = при ценах благ р_x и р_y и доходе потребителя I, мы можем уста­новить оптимальные количества благ х₀ и у₀, имеющих максимальную полезность U₀ (рис. 5.24).

 

 

4. Рассматривая функции издержек (полных затрат) с(q) и дохода фирмы r(q), мы можем ус­тановить зависимость прибыли п(q) = с(q) - r(q) от объема производства q (рис. 5.25) и вы­явить уровни объема производства, при которых производство продук­ции убыточно (0<q<q₂) и приносит прибыль (q₂<q<q₄), дает мак­симальный убыток {q=q₁) и максимальную прибыль (q=q₃) и найти размеры этих убытков или прибыли.

Очевидно, что перечень подобных примеров применения функций в экономической тео­рии и практике можно было бы продолжить.