
 Замена переем: Пусть дана у=в(х) на пром [a,b], х=j(t) непрер и диффер на [a,b]; j(a)=a, j(b)=b
Замена переем: Пусть дана у=в(х) на пром [a,b], х=j(t) непрер и диффер на [a,b]; j(a)=a, j(b)=b
То
Док-во:

 |
 по частям:
по частям:


 Док-во:
Док-во:
Приложения определенного интеграла. Нахождение площади плоской фигуры, длины дуги кривой, объема тела по площадям поперечных сечений и объема тела вращения.
 1)Вычисл площ Пусть дана обл, оганич сверху y=f2(x) и снузу y=f1(x), x=a, x=b:
1)Вычисл площ Пусть дана обл, оганич сверху y=f2(x) и снузу y=f1(x), x=a, x=b:

 2)Выч объма по S сечен: a,b- концы проекц тела на Ох. A=x0£x1£x2...£xn=b. s(c1), S(с) -площ попер сеч. S(c1)Dx1=DV1-объем цилиндр тела с площ основания S(c1) и высотой Dx1.Sn=S(c1)Dx1+…+S(Cn))DXn-объем составного цилиндрич тела. Объем данного тела:
2)Выч объма по S сечен: a,b- концы проекц тела на Ох. A=x0£x1£x2...£xn=b. s(c1), S(с) -площ попер сеч. S(c1)Dx1=DV1-объем цилиндр тела с площ основания S(c1) и высотой Dx1.Sn=S(c1)Dx1+…+S(Cn))DXn-объем составного цилиндрич тела. Объем данного тела:
 Так обр: объем- интеграл от поперечных сечен
Так обр: объем- интеграл от поперечных сечен
 3)V тела вращ: Криволин трапец вращается вокруг Оч, получ тело вращен. Получаемое сечен – круг. r=f(x), S(x)=pf2(x)
3)V тела вращ: Криволин трапец вращается вокруг Оч, получ тело вращен. Получаемое сечен – круг. r=f(x), S(x)=pf2(x)
 11. численные методы интегрирован.
11. численные методы интегрирован.
Разоб отрез а-в на n-равн част. H=x1-x0=x2-x1=...=(b-a)\n
Yi=f(xi)
Ф-ла Лев прямоугольников:
 Ф-ла Прав прямоугольников:
Ф-ла Прав прямоугольников:
 При увеличении nточность формул возрастает.
При увеличении nточность формул возрастает.
Ф-ла трапеций
 |
 Пусть I-точное знач инт, In-приближ знач инт
Пусть I-точное знач инт, In-приближ знач инт
In-I}=D- абсолютная ошибка

 Для трап: D£ где
Для трап: D£ где
 Для прямоуг: D£ где
Для прямоуг: D£ где
Несобственные интегралы
Это опред.интеграл от непрер.ф-ции,но с бескон.промежутком интегрирования иои опред.интеграл с конеч.промеж.интегрирования,но от ф-ции,имеющей на нем бесконечный разрыв.
1)Интеграл по неогранич.обл-ти (бескон.промежутку) 
- ф-ция непрер. на [а;  ).Возьмем на этом промежутке число b.
).Возьмем на этом промежутке число b.  - интегралом от а до
- интегралом от а до 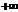 наз-ся lim..,где верхний предел стремится к бесконечности. Если предел сущ-ет,интеграл наз-ся сходящимся, в прот.случае расходящимся.
наз-ся lim..,где верхний предел стремится к бесконечности. Если предел сущ-ет,интеграл наз-ся сходящимся, в прот.случае расходящимся. 

 2) Интегралы по неограниченным областям
2) Интегралы по неограниченным областям
f(x)  +
+  ;x
;x  b-0
b-0


- Выбирая Сn,близкое к b,знач-е интегр.суммы будет сколь угодно большое.Знач.,не будет lim.Выберем точку C и рассм.Sn:  . Если lim сущ-ет,то предел наз-ся сходящимся.
. Если lim сущ-ет,то предел наз-ся сходящимся.
13.Двойной интеграл и его cв-ва. 1) а) Дана ограниче.обл-ть: y=f2(x) сверху,y=f1(x) cнизу. x=a,x=b. Найти площадь фигуры-это площадь разности 2 площадей.


б)Вычисление объема тела по площадям поперечных сечений.

 S(x)-площадь попереч.сечения пл-ти х. a,b-концы проекции тела на ОХ. Разобьем [a,b] на n-частей,в кажд.части возьмем по точке(с1,с2…сn).
S(x)-площадь попереч.сечения пл-ти х. a,b-концы проекции тела на ОХ. Разобьем [a,b] на n-частей,в кажд.части возьмем по точке(с1,с2…сn).  .
.
Тогда S(c1)…S(cn)-площади поперечного сечения в соответ.точках. S(c1)  x1=
x1=  V1-объем цилиндрического тела с площадью основания S(c1) и высотой
V1-объем цилиндрического тела с площадью основания S(c1) и высотой  х1.
х1.
Sn=S(c1)  x1+…+S(cn)
x1+…+S(cn)  xn-объем составной цилиндрической фигуры.
xn-объем составной цилиндрической фигуры. 

Объем-это интеграл от поперечных сечений
2) Дана пластина D(обл-ть на пл-ти).
 -плотность пластины в точке М.
-плотность пластины в точке М.

, где m-масса пластины.Найти массу пластины обл-ти D. Разобьем пластину линиями,парал.осям координат.
Di-части; D1…Dn; в кажд.части берем по точке.
 *
*  S1
S1 

 m1, где
m1, где  S1-площадь части
S1-площадь части  - приближ.знач-е массы пластины D. Переходя к пределам,получим точное знач-е:
- приближ.знач-е массы пластины D. Переходя к пределам,получим точное знач-е: 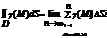
Двойным интегралом от  dS наз-ся предел интегр.суммы
dS наз-ся предел интегр.суммы
Масса пластины-двойной интеграл от  по обл-ти D:
по обл-ти D: 
Cв-ва: 1. св-во линейности: а)  -однородность; б)
-однородность; б)  -адитивность. Теор.существования
-адитивность. Теор.существования 
: Если подынтегр.ф-ция непрер.на замкн.огранич.обл-ти D,то она интегрируема на этой обл-ти.
2. св-во адитивности по обл.интегрирования: Если 
, то 
 14.Геометр.приложения двойных и их вычисление повторным интегрированием
14.Геометр.приложения двойных и их вычисление повторным интегрированием
 -поверхность;
-поверхность;

-интегр.сумма; 
 Si=
Si=  Vi-объем параллелепипеда с площ.основания
Vi-объем параллелепипеда с площ.основания  Si и высотой
Si и высотой 
 - предел инт.суммы может интерпретир.как Vтела.
- предел инт.суммы может интерпретир.как Vтела.
Геом.смысл дв.инт. -это V тела,ограниченного поверх-тью,  фигурой D и некот.цилиндрической поверх-тью по бокам.
фигурой D и некот.цилиндрической поверх-тью по бокам. 
 =
=  ;
; 
D проектируется на ось OX.Для кажд.Х можно говорить о сечении. 
 -
-
это формула повторного интегрирования. 
Дифуры
1.ДУ 1 порядка. Общ и час реш. Зад. Коши. Т-ма сущ и ед реш. З-чи, привод к реш ДУ.
ДУ – Ур-ия, содерж независ переменную, ф-ю от этой переменной и её производные до n порядка включ.: (1) F(x,y,y’,…y(n))=0
Число n (max порядок производ) наз-ся порядком ДУ. Частным решением ДУ (1) наз. ф-ия, при подстав кот. ур-ие превращ в тождество.Мн-во всех част.решений. наз-ют общим реш. ДУ
ДУ (2) y(n)=f(x,y,y’…y(n-1)) наз-ся разрешенным относит-но старшей производной. Задача нахожд реш-й Д У наз-ся интегрирированием Д У.
F (x,y,y’)=0; (2) y’=f(x;y)-разреш.отн-но производной
(3)P(x,y)dx+Q(x,y)dy=0-симметрич.форма записи ДУ
y’=dy/dx; dy/dx=f(x,y); dy=f(x,y)dx; f(x,y)dx-dy=0.
В ур-ии (3) можно искать ф-ю y(x) или x(y). Рассм (2) ур-е:
касательная в точке
tgα=f(x,y’)
Задача Коши:
y’=f(x,y); (4)
y|x=x0=y0.
Найти част.реш-я ур-ия,удовл начал усл-ям, т е знач-я ф-ии при x=x0 равно y=y0.
Теор. сущ-я: пусть ф-я f(x,y), f ‘y(x,y) – непр в некот.окрес-ти (.)U(x0,y0)=U(Mo), тогда сущ-ет такая окрест U(x0) и ф-ция y=y(x), заданная в этой окрест-ти,такие, что ф-ция y(x) явл реш з-чи (4),т.е. y(x0)=y0; y(x) удоветв. y’=f(x,y) в окрест-ти точки M0. Такая ф-ия y(x) сущ-ет только одна.
Обл.D непрерывности ф-ции,f’y-непр. Есть точка M0 из обл.D.
y’=ky; f(x,y) =ky; f’y=k. Обе ф-ции непрер.на всей пл-ти,и знач.,решением будет y=cekt; y|x=0 =с M(0,c) и оно будет ед реш, проход. через (.) М(0;с)
 2. ДУ с разделяющ и разделён перем-ми.
2. ДУ с разделяющ и разделён перем-ми.
(*)P(x)dx+Q(y)dy=0 – ДУ с разделенными пер-ми.
y=y(x)=> Q(y)dy=Q(y)y’(x)dx; ∫P(x)dx+∫Q(y)y’(x)dx=C; ∫P(x)dx+∫Q(y)y’(x)dx=C; ∫P(x)dx+∫Q(y)dy=C –это общее реш.(общ.интеграл ДУ)
(**)m1(x)n1(y)dx+m2(x)n2(y)dy=0 – ДУ с разделяющ пер-ми. (m1(x)/m2(x))dx+(n1(y)/n2(y))dy=0 – ДУ с разделён пер-ми.
– общий интеграл.
3. ЛДУ 1 порядка.
ЛДУ 1 п-ка – ур-ия вида y’+p(x)y=q(x).
Реш-е: будем искать реш как произвед 2 ф-ций:
y=u(x)*v(x); y’=u’v+uv’; u’v +uv’+ puv =q; (u’+pu)v+uv’=q(*);
усл-е: u’+pu=0; (u’)=du/dx=-pu; du=-pudx; du/u=-pdx.
Проинтегрируем по х: 
 =-∫p(x)dx;
=-∫p(x)dx;
u=e-∫p(x)dx;
e-∫p(x)dxv’=q(x)
 4.Численное решение дифференциального уравнения. Метод Эйлера.
4.Численное решение дифференциального уравнения. Метод Эйлера.
Ишем решение (ДУ) на [x0; b] = [a;b]

H=(b-a)/n; h – шаговое разделение
| x | y | |
| a= | X0 | Y0 |
| X1 | Y1 | |
| ... | … | |
| b= | Xn | Yn |
y’=f(x0;y0)

y(x+h)=y(x) + h*y(x) (*)(*) исходя из определения производной получаем:у1=y(x0+h)≈y(x0)+h*f(x0;y0);у2=y(x1+h)≈y(x1)+h*f(x1;y1). В ответе имеем таблично заданную функцию которая тем ближе к табличному решению, чем меньше число h. Метод Эйлера. Приближенное решение нашего ДУ. Способ оценивания ошибок 1) max | y(x) – yn (x)| x є [a;b] 2) | ỹ(b) – yn (b)| ỹn(x); ỹ2n(x) | ỹn - ỹ2n|. Если данная величина мала, то полученное решение является «достаточно» точным. Задачи оценки кач-ва намного сложнее, чем нахождение решения.
5. ДУ высших порядков. Общее и частное решение. Задача Коши. Теорема существования и единственности решения.
F(x, y, y’…y(n))=0; y(n)=f(x, y, y’…y(n-1)). Решение: 1) общее y=φ(x, c1…cn) мн-во всех решений. 2) частное y=y(x) ф-ия, при подстан. кот. получ. верное тождество. Задача Коши

теорема существования и единственности. Пусть нам дана задача Коши и пусть ф-ии f, f’y…f’y(n-1) непр. M0 (x0, y0, y’0…y0n-1). Тогда сущ. Ux0 и ф-ия y=y(x) определённая в этой окрестности такая что она явл. Решением задачи Коши. Такая ф-ия сущ. только одна.
6. Линейный дифференциальный оператор n-го порядка и его свойства. Свойства решений линейного однородного дифференциального уравнения.
Линейный диф. оператор

Свойства


Доказательство 
Исследуем множество решений линейного однородного уравнения, являющегося векторным пространством. Множество функции задано на [a;b] λf(x); f(x)+g(x); (f+g)+h=f+(g+h) – ассоц.; f+g=g+f – Коммут.; f+0=f; f+(-f)=0 т.о. мн-во функции является вектором пространства L[y]=0; 1) y - решение=>λy – решение L[λy]= λL[y]=0; 2)y1, y2 – решение; L[y1]= L[y2]=0 => y1 + y2 – решение; L[y1+y2]= L[y1]+ L[y2]=0
На множестве решений можно определить две операции. Множество решений однородного линейного уравнения является векторное пространство
 7. Фундаментальная система решений, для линейного однородного уравнения. Определитель Вронского.
7. Фундаментальная система решений, для линейного однородного уравнения. Определитель Вронского.
Фундаментальная система называется всякий базис множества y.- фун-ия линейно независима (y1….yn)- при добавлении любой другой функции становится линейно зависима (для любого y, y1…yn, y
Рассмотрим ДУ второго порядка
Если λ1≠ λ2 И это вещественное число => W≠0 и => функция y1 и y2 – линейнонезавис. И сост. Фунд. Сист. Реш. Y=c1y1+c2y2 =c1eλ1+c2 eλ2
Дадим определение определителя Вронского
Т1: если y1, y2… yn лин. зависимы, то W(x)=0 для xєX. мн-во – это интервал опред. коэф. ур-я L[y]=0. Т2: если W(x0)=0, то W(x)=0 для всех xєX:u y1, y2… yn – лин. завис. Т3: если W(x0) ≠0, то W(x) ≠0 при любом x єX. W(x0)=0 => по Т.2 W(x)=0 при любом xєX. Т4: Для ДУ сущ. m линейно-независ. ф-ий y1, y2… yn. Нач. ус ловие x=x0. получ. Единичн. Матр. Δ=1=> этим ф-ии лин.независ. Т5: пусть y1, y2… yn. линейно независ. y – произв.
 8. теорема о структуре общего решения линейного неоднородного ДУ n-го порядка.
8. теорема о структуре общего решения линейного неоднородного ДУ n-го порядка.
Теорема: общее решение ЛНДУ n-го порядка равно сумме частного решения y* неоднородного уравнения и общего решения ŷ соответствующего ему однородного уравнения, т. е. y=y*+ ŷ.
Частное решение y* ЛНДУ n-го порядка может быть найдено, если известно общее решение ŷ однородного уравнения, методом вариации произвольных постоянных. Оно ищется в виде: y*= c1(x)y1(x)+ c2(x)y2(x)+…+ cn(x)yn(x), yi(x), i=от 1 до n- частные решения, образующие фундаментальную систему, однородного уравнения.
Система уравнений для нахождения неизвестных ci(x) имеет вид:
Однако для ЛНДУ n-го порядка с пост. коэф., правая часть которого имеет спец. вид, частное решение y* может быть найдено методом неопределённых коэффициентов. Метод подбора частного решения y* уравнения y(n)+p1y(n-1)+…+pny=f(x), где pi – числа, а правая часть f(x) имеет специальный вид.
10.Линейные ДУ с пост. коэф. И его характеристическое уравнение. Вид общего решения в случае различных корней характ. ур-я. (на примере ДУ второго порядка)
Частным случаем однородных ДУ уравнений являются ЛОДУ с пост. коэф. Пусть дано ЛОДУ второго порядка: y’’+p•y’+q•y=0; где p и q постоянны. Для нахождения общего решения уравнения достаточно найти два его частных решения, образующих фундаментальную систему. Будем искать частные решения уравнения в виде y=ekx, где k-некоторое число. Дифференцируя эту функцию два раза и подставляя выражения для y, y’ и y’’ в данное уравнение, получим k2ekx+pkekx+qekx=0, т.е ekx(k2+pk+q)=0 или k2+pk+q=0 (ekx≠0)-характеристическое уравнением ДУ. При его решении возможны следующие три случая. Случай 1: корни k1 и k2 данного Ур-я действительные и различные:  . В этом случае частными решениями уравнения являются функции y1=ek1x и y2=ek2 x. Они образуют фундаментальную систему решений, т. к.
. В этом случае частными решениями уравнения являются функции y1=ek1x и y2=ek2 x. Они образуют фундаментальную систему решений, т. к.  . Следовательно, общее решение уравнения имеет вид: y=c1ek1x+ c2ek2x.
. Следовательно, общее решение уравнения имеет вид: y=c1ek1x+ c2ek2x.