Любая статистическая работа начинается со статистического наблюдения, представляющего собой массовое, планомерное, научно организованное наблюдение за явлениями социальной и экономической жизни, заключающееся в регистрации отобранных признаков у каждой единицы совокупности. Сбор статистических данных производится по специальным правилам статистического наблюдения.
Результаты статистического наблюдения представляют собой числовую информацию – данные. Статистические данные – это сведения о том, какие значения приняли интересующие аналитика признаки. Значения признака при переходе от одного элемента к другому изменяются (варьируют), поэтому в статистике различные значения признака также называют вариантами.
Статистический материал, получающийся в результате наблюдений (измерений), можно записать в виде таблицы, состоящей из двух строк. В первой строке отмечаются номера измерений, во втором – полученные значения. Такая таблица называется простым статистическим рядом:
| … | i | … | n | ||
| x 1 | x 2 | … | xi | … | xn |
Важнейшим этапом исследования социально-экономических явлений и процессов является систематизация первичных данных и получение на этой основе сводной характеристики объекта в целом при помощи обобщающих показателей. Однако при большом числе измерений статистический ряд трудно анализировать. Поэтому результаты наблюдений необходимо каким-либо образом упорядочить. Для этого наблюдаемые значения располагают в порядке их возрастания (ранжируют):
x 1, x 2, …, xn,
где xi £ xi +1. Такой статистический ряд называется ранжированным.
Одним из основных наиболее распространенных методов обработки и анализа первичной статистической информации является группировка. Если некоторые значения статистического ряда имеют одинаковые значения, то их можно объединить. Тогда каждому значению xi будет соответствовать число ni, равное частоте появлений данного значения:
| x 1 | x 2 | … | xi | … | xk |
| n 1 | n 2 | … | ni | … | nk |
Такой ряд называется сгруппированным.
Ранжированный и сгруппированный статистический ряд называется вариационным, т.е. вариационный ряд имеет вид
| x 1 | x 2 | … | xk |
| n 1 | n 2 | … | nk |
где x 1< x 2<…< xk. Наблюдаемые значения xi называются вариантами, а число наблюдений варианты ni – частотой. Число всех наблюдений n называется объёмом вариационного ряда.
Кроме дискретных вариационных рядов, применяются и интервальные вариационные ряды. Для построения такого ряда необходимо определить величину интервалов и в соответствии с ними сгруппировать результаты наблюдений:
| [ x 1; x 2] | (x 2; x 3] | (x 3; x 4] | … | (xk –1; xk ] |
| n 1 | n 2 | … | … | nk |
Интервальный вариационный ряд строят обычно в тех случаях, когда число наблюдавшихся вариантов очень велико. Обычно такая ситуация возникает при наблюдениях за непрерывной случайной величиной (например, при измерениях какой-либо физической величины).
Между интервальными и дискретными вариационными рядами существует определенная взаимосвязь. Любой дискретный ряд можно записать в виде интервального и наоборот. Например, интервальный ряд можно представить в виде дискретного, если в качестве вариант (наблюдаемых значений) взять середины интервалов. Отметим, что, вообще говоря, при группировке наблюдаемых значений в виде интервального ряда теряется часть информации, в результате чего погрешность вычислений, основанных на таком ряде, возрастает.
Для графического описания дискретного вариационного ряда используют полигон. Для построения полигона в прямоугольной системе координат наносят точки с координатами (xi, ni). Затем эти точки соединяют отрезками. Полученная ломаная линия называется полигоном (рис. 3.1а).
Для графического описания интервального вариационного ряда используют гистограмму. Для ее построения по оси абсцисс откладывают отрезки, изображающие интервалы варьирования, и на этих отрезках, как на основании, строят прямоугольники с высотами, равными частотам или относительным частотам соответствующего интервала. В результате получается фигура, состоящая из прямоугольников, которая и называется гистограммой. (рис. 3.1б).
а
| 
б
|
| Рис. 3.1 |
Построение вариационного ряда – лишь первый шаг к осмыслению наблюдений. Этого недостаточно для полного исследования распределения изучаемого явления. Наиболее удобным и полным является аналитический способ исследования ряда, состоящий в установлении числовых характеристик. Числовые характеристики, применяемые для исследования вариационных рядов, аналогичны тем, которые применяют в теории вероятностей (математическое ожидание, дисперсия, центральные и начальные моменты и др.), только нужно понятие «вероятность» заменить понятием «относительная частота».
Наиболее естественной характеристикой вариационного ряда является понятие средней величины. В статистике используют несколько видов средних величин: среднее арифметическое, среднее геометрическое, среднее гармоническое и др. Наиболее распространенным является понятие среднее арифметическое.
Если дан простой статистический ряд, то средняя арифметическая величина вычисляется по формуле
. (3.1)
Если по данным наблюдений построен вариационный ряд, то используется понятие средней взвешенной арифметической величины:
. (3.2)
В качестве меры рассеяния значений наблюдаемой величины вокруг своего среднего значения принимают величину
, (3.3)
которую, как и в теории вероятностей, называют дисперсией. Статистическая дисперсия обладает теми же самыми свойствами, что и вероятностная дисперсия, и для ее вычисления можно использовать альтернативную формулу
(3.4)
Величина
(3.5)
называется средним квадратичным отклонением (или стандартным отклонением).
Начальным моментом hk порядка k называется число
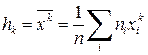. (3.6)
В частности, 
.
Центральным моментом mk порядка k называется число
. (3.7)
В частности, 
.
Между центральными и начальными моментами существует взаимосвязь:
, 
, 
. (3.8)
На практике чаще всего используются моменты 3-го и 4-го порядка (кроме, конечно, среднего значения и дисперсии). Момент 3-го порядка используют для вычисления коэффициента асимметрии:
. (3.9)
Если распределение значений признака симметрично относительно среднего значения, то A =0. Если правосимметрично (т.е. преобладают значения x, больше 
), то A >0. Если левосимметрично (т.е. преобладают значения x, меньше ), то A <0.
Момент 4-го порядка используется для вычисления эксцесса:
. (3.10)
Для распределений близких к нормальному E =0. При E >0 распределение называют островершинным, при E <0 – плосковершинным.
Вычисление среднего арифметического, дисперсии и, особенно, моментов высших порядков непосредственно по их формулам приводит к громоздким вычислениям, если числовые значения достаточно велики. Поэтому воспользуемся упрощенным методом расчета моментов. Для этого все значения дискретного вариационного ряда преобразуем по формуле
. (3.11)
Постоянные L и C выбираются произвольно. Обычно в качестве C выбирают значение, которое имеет наибольшую частоту или занимает среднее положение в ряду. В качестве L можно взять длину интервала.
По упрощенному методу сначала вычисляют среднее значение и начальные моменты для новой переменной u, а затем находятся искомые значения для среднего значения 
и начальные моменты 
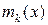по формулам
, 
. (3.12)
Пример 3.1. Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда:
| x | 582-589 | 589-596 | 596-603 | 603-610 | 610-617 |
| n | |||||
| x | 617-624 | 624-631 | 631-638 | 638-645 | 645-652 |
| n |
Вычислить среднее арифметическое значение, дисперсию, среднее квадратичное отклонение, коэффициенты асимметрии и эксцесса, используя упрощенный метод вычислений.
Решение. Вначале вместо интервального ряда введем дискретный, взяв вместо интервалов только их середины, а результаты занесем в таблицу.
| xi | ni | ui | niui | 
| 
| 
|
| 585,5 | –4 | –16 | –256 | |||
| 592,5 | –3 | –15 | –135 | |||
| 599,5 | –2 | –12 | –48 | |||
| 606,5 | –1 | –12 | –12 | |||
| 613,5 | ||||||
| 620,5 | ||||||
| 627,5 | ||||||
| 634,5 | ||||||
| 641,5 | ||||||
| 648,5 | ||||||
| S |
По упрощенному методу вводим новую переменную (см. формулу 3.11):
.
Здесь в качестве С= 613,5 взято значение из середины ряда, а в качестве L= 7 – длина интервалов. Далее, в соответствии с данными таблицы получаем
,
.
Найдем начальные моменты по данным таблицы:
, 
,
, 
.
После этого вычисляем центральные моменты:
,
.
Зная моменты 3-го и 4-го порядков, можно вычислить коэффициент асимметрии и эксцесс:
, 
.
Асимметрия положительна, следовательно, распределение характеризуется незначительной правосторонней асимметрией. Отрицательный эксцесс указывает на более плосковершинное распределение по сравнению с нормальным.