Под статистической гипотезой H понимают любое предположение о генеральной совокупности (случайной величине), проверяемое по выборке. Это может быть предположение о виде распределения генеральной совокупности, о равенстве двух выборочных дисперсий, о независимости выборок, об однородности выборок, что закон распределения не меняется от выборки к выборке и др.
Гипотеза называется простой, если она однозначно определяет какое-либо распределение или какой-либо параметр; в противном случае гипотеза называется сложной. Например, простой гипотезой является предположение о том, что случайная величина X распределена по стандартному нормальному закону N (0;1); если же высказывается предположение, что случайная величина X имеет нормальной распределение N (m;1), где a £ m £ b, то это сложная гипотеза.
Проверяемая гипотеза называется основной или нулевой гипотезой и обозначается символом H 0. Наряду с основной гипотезой рассматривают и противоречащую ей гипотезу, которую обычно называют конкурирующей или альтернативной гипотезой и обозначают символом H 1. Если основная гипотеза будет отвергнута, то имеет место альтернативная гипотеза. Например, если проверяется гипотеза о равенства параметра q некоторому заданному значению q0, т.е. H 0:q=q0, то в качестве альтернативной гипотезы можно рассмотреть одну из следующих гипотез: H 1:q>q0, H 2:q<q0, H 3:q¹q0, H 4:q=q1. Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.
Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверка осуществляется статистическими методами, то в связи с этим с определенной долей вероятности может быть принято неправильное решение. Здесь могут быть допущены ошибки двух видов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Вероятность ошибки первого рода обозначают буквой a, т.е.
 .
.
Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Вероятность ошибки второго рода обозначают буквой b, т.е.
 .
.
Последствия указанных ошибок неравнозначны. Первая приводит к более осторожному, консервативному решению, вторая – к неоправданному риску. Что лучше или хуже – зависит от конкретной постановки задачи и содержания нулевой гипотезы. Например, если H 0 состоит в признании продукции предприятия качественной и допущена ошибка первого рода, то будет забракована годная продукция. Допустив ошибку второго рода, мы отправим потребителю брак. Очевидно, что последствия ошибки второго рода более серьезны с точки зрения имиджа фирмы и ее долгосрочных перспектив.
Исключить ошибки первого и второго рода невозможно в силу ограниченности выборки. Поэтому стремятся минимизировать потери от этих ошибок. Отметим, что одновременное уменьшение вероятностей данных ошибок невозможно, т.к. задачи их уменьшения являются конкурирующими. И снижение вероятности допустить одну из ошибок влечет за собой увеличение вероятности допустить другую ошибку. В большинстве случаев единственный способ уменьшения обеих вероятностей состоит в увеличении объема выборки.
Правило, в соответствие с которым принимается или отклоняется основная гипотеза, называется статистическим критерием. Для этого подбирается такая случайная величина K, распределение которой точно или приближенно, известно и которая служит мерой расхождения между опытными и гипотетическими значениями.
Для проверки гипотезы по данным выборки вычисляют выборочное (или наблюдаемое) значение критерия K набл. Затем, в соответствии с распределением выбранного критерия, строится критическая область K крит. Это такая совокупность значений критерия, при которых нулевую гипотезу отвергают. Оставшуюся часть возможных значений называют областью принятия гипотезы. Если ориентироваться на критическую область, то можно совершить ошибку
1-го рода, вероятность которой задана заранее и равна a, называемой уровнем значимости гипотезы. Отсюда вытекает следующее требование к критической области K крит:
 .
.
 |
Уровень значимости a определяет "размер" критической области K крит. Однако ее положение на множестве значений критерия зависит от вида альтернативной гипотезы. Например, если проверяется нулевая гипотеза H 0:q=q0, а альтернативная гипотеза имеет вид H 1:q>q0, то критическая область будет состоять из интервала (K2, +¥), где точка K2 определяется из условия P (K>K2)=a (правосторонняя критическая область). Если альтернативная гипотеза имеет вид H 2:q<q0, то критическая область будет состоять из интервала (–¥;K1), где точка K1 определяется из условия P (K<K2)=a (левосторонняя критическая область). Если альтернативная гипотеза имеет вид H 3:q¹q0, то критическая область будет состоять из двух интервалов (–¥;K1) и (K2, +¥), где точки K1 и K2 определяются из условий: P (K>K2)=a/2 и P (K<K2)=a/2 (двухсторонняя критическая область) (рис.3.2).
Основной принцип проверки статистических гипотез можно сформулировать следующим образом. Если K набл попадает в критическую область, то гипотеза H 0 отвергается и принимается гипотеза H 1. Однако поступая таким образом, следует понимать, что здесь можно допустить ошибку 1-го рода с вероятностью a. Если K набл попадает в область принятия гипотезы – то нет оснований, чтобы отвергать нулевую гипотезу H 0. Но это вовсе не означает, что H 0 является единственно подходящей гипотезой: просто расхождения между выборочными данными и гипотезой H 0 невелико. Однако таким же свойством могут обладать и другие гипотезы.
Критерии, используемые для проверки гипотез о параметрах распределения, называются критериями значимости. В частности, построение критической области аналогично построению доверительного интервала. Критерии, используемые для проверки согласия между выборочным распределением и гипотетическим теоретическим распределением, называются критериями согласия.
Общая схема статистической проверки гипотез:
1. Формулируется основная H 0 и альтернативная H 1 гипотезы.
2. Выбирается соответствующий уровень значимости a.
3. Определяется объем выборки n.
4. Выбирается критерий K для проверки H 0.
5. Определяется критическая область и область принятия решения (в соответствии с выбранной альтернативной гипотезой).
6. Вычисляется наблюдаемое значение критерия K набл (по данным выборки).
7. Принимается статистическое решение. Если K набл попадает в область принятия решений, то нет оснований отклонять основную гипотезу, и она принимается. Если K набл попадает в критическую область, то основная гипотеза отвергается.
Пример 3.5. Утверждается, что шарики, изготовленные станком-автоматом, имеют средний диаметр d 0=10 мм. В выборке из n =16 шариков средний диаметр оказался равным  мм. Проверить нулевую гипотезу H 0:
мм. Проверить нулевую гипотезу H 0:  , считая, что дисперсия известна и равна s2=1 мм 2. Считать уровень значимости a=0,05.
, считая, что дисперсия известна и равна s2=1 мм 2. Считать уровень значимости a=0,05.
Решение. Введем статистический критерий:
 ,
,
который при справедливости нулевой гипотезы H 0, имеет стандартное нормальное распределение N (0;1). Пусть альтернативная гипотеза имеет вид H 1:  , то критическая область будет иметь двухсторонний вид: (–¥;– Zкрит)È(Zкрит;+¥), где Zкрит определяется из условия
, то критическая область будет иметь двухсторонний вид: (–¥;– Zкрит)È(Zкрит;+¥), где Zкрит определяется из условия
 ,
,
или
 .
.
Критическое значение Zкрит находится из таблиц значений функции Лапласа (см. приложение 2).
Поскольку

не попадает в критическую область, то нет оснований отклонять нулевую гипотезу, т.е. что шарики, изготовленные станком-автоматом, имеют средний диаметр 10 мм.
Пример 3.6. Анализируются доходы X фирм в отрасли, имеющих нормальное распределение. Предполагается, что средний доход в данной отрасли составляет не менее 1 млн $. По выборке из 49 фирм получены следующие данные:  млн $ и s =0,15 млн $. Не противоречат ли эти результаты выдвинутой гипотезе при уровне значимости a=0,01?
млн $ и s =0,15 млн $. Не противоречат ли эти результаты выдвинутой гипотезе при уровне значимости a=0,01?
Решение. Сформулируем основную и альтернативную гипотезы:
 ,
, 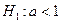 .
.
Для проверки гипотезы H 0 строим критерий
 .
.
Критическая область будет левосторонней, поэтому
 .
.
Поскольку Tнабл =–4,67<–2,404= Tкрит, то H 0 должна быть отклонена в пользу H 1, что дает основание считать, что средний доход в отрасли меньше, чем 1 млн $.
Часто функция распределения случайной величины бывает заранее неизвестна, и возникает необходимость ее определения по эмпирическим данным. Во многих случаях из некоторых дополнительных соображений могут быть сделаны предположения о виде функции распределения F (x). На практике часто используют нормальное распределение, однако в некоторых случаях может возникнуть вопрос о законности использования нормального распределения в том или ином конкретном случае. В таких случаях нужно использовать статистические критерии, которые обосновывали бы тот или иной выбор распределения.
Наиболее распространенным является c2–критерий Пирсона. Рассмотрим этот критерий. Для этого разобьем множество значений случайной величины X на r интервалов S 1, S 2, …, Sr. Пусть pi – вероятность того, что величина X принадлежит интервалу Si; ni – количество величин из числа наблюдаемых X 2, …, Xn, принадлежащих интервалу Si. Далее рассматривается величина
 , (3.22)
, (3.22)
При достаточно больших n эта величина будет описываться c2–распределением Пирсона с n = r– 1 -m, где m – число параметров распределения (для нормального распределения m =2).
Отметим, что критерий Пирсона применяется только при достаточно больших выборках (n t50) и достаточно больших частотах (ni ³5). Если последнее условие не выполняется для какого-либо интервала вариационного ряда, то его объединяют с соседним интервалом, соответственно уменьшая общее число интервалов.
Схема применения критерия согласия Пирсона:
1. Вычисляются параметры предполагаемого закона распределения.
2. Вычисляются теоретические частоты 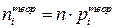 .
.
3. Вычисляют величину
4.  .
.
5. По вычисленному числу степеней свободы n= r –1– m, где r – число интервалов выборки, m – число параметров распределения и по выбранному уровню значимости a по таблицам распределения c2, находят  .
.
6. Если  , то нет оснований отклонять нулевую гипотезу, если
, то нет оснований отклонять нулевую гипотезу, если  – нулевая гипотеза отвергается.
– нулевая гипотеза отвергается.
Пример 3.7.: Используя коэффициенты асимметрии и эксцесса, сделать соответствующие предположения о виде функции распределения генеральной совокупности по данным примера 3.1. Используя критерий Пирсона, проверить гипотезу о нормальности распределения генеральной совокупности при уровне значимости a=0,05.
Решение. Определим значимость коэффициентов асимметрии и эксцесса, вычисленных в примере 1. Для этого вычислим погрешность вычислений по формулам
 ,
,
 .
.
Посмотрим теперь, попадают ли найденные значения в «трехсигмовый» интервал:
 ,
,  .
.
Из полученных неравенств следует, что коэффициент асимметрии и эксцесс не значимо отличаются от нуля и есть все основания полагать, что распределение генеральной совокупности является нормальным.
В соответствии с критерием Пирсона сначала вычисляется величина
 ,
,
где pi – вероятности, полученные по предполагаемому закону распределения. Ёще раз повторим, что c2-распределение можно применять только при достаточно большом объеме выборки (n t50) и достаточно больших частотах (ni ³5). Ту группу вариационного ряда, для которых последнее условие не выполняется, объединяют с соседней и, соответственно, уменьшают число интервалов. В рассматриваемом случае мы должны объединить интервалы 1 и 2, а также 9 и 10 (см. таблицу).
| i | xi – xi +1 | ni | 
| 
| 
| 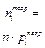
| 
|
 1 1
| 582-589 | –0,4131 | –0,4887 | 0,0756 | 6,804 | 0,709 | |
| 589-596 | |||||||
| 596-603 | –0,3159 | –0,4131 | 0,0972 | 8,748 | 0,863 | ||
| 603-610 | –0,1700 | –0,3159 | 0,1459 | 13,131 | 0,097 | ||
| 610-617 | 0,0080 | –0,1700 | 0,1780 | 16,020 | 1,562 | ||
| 617-624 | 0,1844 | 0,0080 | 0,1764 | 15,876 | 0,080 | ||
| 624-631 | 0,3264 | 0,1844 | 0,1420 | 12,780 | 1,118 | ||
| 631-638 | 0,4192 | 0,3264 | 0,0928 | 8,352 | 0,219 | ||
 9 9
| 638-645 | ||||||
| 645-652 | 0,4898 | 0,4192 | 0,0706 | 0,0706 | 1,102 | ||
| 0,9785 | 88,065 | 5,750 |
В предположении, что имеет место нормальное распределение, были оценены два параметра этого распределения:  и
и  . Если изучаемое распределение подчинено нормальному распределению, то вероятность того, что случайная величина X примет значение из интервала (xi < X < xi +1), находится по формуле
. Если изучаемое распределение подчинено нормальному распределению, то вероятность того, что случайная величина X примет значение из интервала (xi < X < xi +1), находится по формуле
 .
.
где  – функция Лапласа, значения которой табулированы и приводятся в таблицах.
– функция Лапласа, значения которой табулированы и приводятся в таблицах.
Из расчетной таблицы видно, что
 .
.
Теперь найдем критическое значение  . Поскольку у предполагаемой модели были неизвестны оба параметра, поэтому m =2; при расчете критерия использовались восемь интервалов r =8. Таким образом, число степеней свободы n= r –1– m =5. При заданном уровне значимости из таблиц для c2-распределения находим
. Поскольку у предполагаемой модели были неизвестны оба параметра, поэтому m =2; при расчете критерия использовались восемь интервалов r =8. Таким образом, число степеней свободы n= r –1– m =5. При заданном уровне значимости из таблиц для c2-распределения находим
 .
.
Поскольку 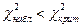 , то нет оснований отвергать нулевую гипотезу, т.е. что исходное распределение является нормальным.
, то нет оснований отвергать нулевую гипотезу, т.е. что исходное распределение является нормальным.