Проблема изучения взаимосвязей экономических показателей является одной из важнейших проблем экономического анализа. Любая экономическая политика заключается в регулировании экономических переменных (показателей), и она должна основываться на знании того, как эти переменные влияют на другие переменные, являющиеся ключевыми для принимающего решения предпринимателя или политика. Так, в рыночной экономике нельзя непосредственно регулировать темп инфляции, но на него можно воздействовать средствами фискальной (бюджетно-налоговой) и монетарной (кредитно-денежной) политики. Поэтому, в частности, должна быть изучена зависимость между предложением денег и уровнем цен. Вся сфера экономических исследований может быть в определенном смысле охарактеризована как изучение взаимосвязей экономических переменных.
В природе связи между различными явлениями сложны и многообразны. В естественных науках часто идет речь о функциональной зависимости, когда каждому значению одной переменной соответствует вполне определенное значение другой переменной. В экономической науке также часто имеют дело с функциональными зависимостями. Различные экономические показатели как на микро-, так и на макроуровне не являются независимыми, а связаны между собой функциональной зависимостью. Например, цена какого-либо товара и величина спроса на этот товар; объем производства и прибыль фирмы; инфляция и безработица и т.д.
Однако не всякая зависимость между двумя переменными является функциональной. В реальном мире многие явления природы происходят в обстановке действия многочисленных факторов, влияние каждого из которых ничтожно, а число их велико. В этих случаях связь теряет свою строгую функциональность. Физическая система, например, переходит из одного состояния в другое, но не строго определенное, а в одно из возможных для нее состояний. Здесь речь может идти лишь о так называемой стохастической (вероятностной, статистической) зависимости. В экономике также в основном имеют дело со стохастическими зависимостями, поскольку на интересующий нас тот или иной показатель кроме явно учитываемых переменных влияют еще и много других, не учтенных явно в модели. Это обуславливает стохастическую природу многих экономических переменных. Например, рост дохода ведет к увеличению потребления; снижение процентной ставки увеличивает инвестиции; увеличение валютного курса сокращает чистый экспорт. Все эти зависимости – стохастические, поскольку по значениям одной переменной нельзя определить точное значение другой переменной.
Стохастическая зависимость проявляется в том, что при изменении одной из величин изменяется математическое ожидание (среднее значение) другой, в таких случаях говорят о корреляционной зависимости. Например, очевидно, что при увеличении высоты деревьев в среднем растут и диаметры стволов. Очевидно, что корреляционная зависимость является частным случаем стохастической связи. Знание корреляционной зависимости между случайными величинами имеет большое практическое значение: с ее помощью можно прогнозировать значение зависимой случайной переменной в предположении, что независимая переменная примет определенное значение. Однако, поскольку понятие корреляционной зависимости относится к случайным величинам, прогнозы не могут быть безошибочными. Применяя некоторые вероятностные методы, можно вычислить вероятность того, что ошибка прогноза не выйдет за определенные границы.
Для изучения влияния независимой переменной X на объясняемую переменную Y используют «усредненные» зависимости, т.е. изучают условное математическое ожидание M[ Y | x ] (математическое ожидание случайной величины, вычисленную в предположении, что переменная X приняла значение x) в зависимости от x. Поскольку при различных значениях будут получаться различные значения условного математического ожидания, то мы будем иметь дело с некой функцией
 , (3.24)
, (3.24)
которая называется функцией регрессии Y на X.
Для отражения того факта, что реальные значения зависимой переменной не всегда совпадают с ее условными математическими ожиданиями и могут быть различными при одном и том же значении объясняющей переменной, фактическая зависимость должна быть дополнена некоторым слагаемым e, которое, по существу, является случайной величиной и указывает на стохастическую суть зависимости. Величину e обычно называют случайным отклонением (ошибкой, возмущением). Из этого следует, что связь между зависимой и объясняющей переменной выражается соотношением
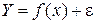 , (3.25)
, (3.25)
называемое регрессионной моделью (теоретическим уравнением регрессии).
Используя выборочные данные можно построить так называемое эмпирическое уравнение регрессии:
 , (3.26)
, (3.26)
где отклонение ei – оценка теоретического случайного отклонения e i. Эту величину также называют остатками.
Идея метода наименьших квадратов (МНК) основана на том, чтобы минимизировать сумму квадратов отклонений расчетных значений от эмпирических, т.е. нужно оценить параметры q функции f (x,q) таким образом, чтобы отклонения  , точнее – их квадраты, по совокупности были минимальны. Для этого нужно решить задачу минимизации
, точнее – их квадраты, по совокупности были минимальны. Для этого нужно решить задачу минимизации
 . (3.27)
. (3.27)
Из необходимых условий экстремума функции Q, т.е. равенства нулю частных производных функции Q по каждому из параметров q, получим
 . (3.28)
. (3.28)
В результате получается нормальная система алгебраических уравнений, решая которую можно найти неизвестные параметры q.
Пусть по выборке (xi, yi) требуется определить оценки коэффициентов a и b обобщённого линейного уравнения регрессии
 . (3.29)
. (3.29)
В соответствии с МНК, нужно выбрать параметры a и b таким образом, чтобы минимизировать сумму:
 . (3.30)
. (3.30)
Из необходимых условий существования минимума функции двух переменных (3.29) получаем следующую систему нормальных уравнений:
 (3.31)
(3.31)
Более сложной проблемой является применение МНК для моделей, нелинейных по параметрам. В ряде случаев путем подходящих преобразований эти модели удается привести к линейной форме. Например, степенную модель 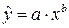 при помощи логарифмического преобразования можно привести к линейному виду:
при помощи логарифмического преобразования можно привести к линейному виду:
 .
.
Пример 3.8. Методом наименьших квадратов подобрать функцию 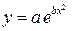 по табличным данным и сделать чертеж.
по табличным данным и сделать чертеж.
| x | |||||||
| y |
Решение. В соответствие с методом наименьших квадратов (МНК) следует подобрать коэффициенты a и b таким образом, чтобы функция

приняла минимальное значение. Необходимым условием экстремума функции Q является равенство нулю всех частных производных по неизвестным параметрам. Чтобы упростить вычисления вместо искомой функции рассмотрим ее логарифм
 .
.
Тогда
 или
или 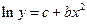 .
.
Функция Q будет иметь вид
 .
.
Составляем систему нормальных уравнений

Отсюда находим
 и
и  .
.
Далее, составим таблицу вычислений:
| № | x | y | ln y | x 2 | x 4 | x 2ln y | 
|
| 6,985 | 0,000 | 1064,3 | |||||
| 6,841 | 27,362 | 947,1 | |||||
| 6,585 | 105,357 | 667,5 | |||||
| 5,892 | 212,099 | 372,6 | |||||
| 5,170 | 330,911 | 164,7 | |||||
| 3,761 | 376,120 | 57,7 | |||||
| 2,944 | 423,999 | 16,0 | |||||
| Среднее значение | 5,454 | 210,836 |
По данным таблицы находим
 ,
,  ,
,

Таким образом, искомая функция имеет вид
 .
.
Изобразим на рисунке исходные данные (квадратики) и график искомой кривой:
 |
Приложение 1
Плотность функции нормального распределения 
| ||||||||||
| 0,0 | 0,3989 | 0,3989 | 0,3989 | 0,3988 | 0,3986 | 0,3984 | 0,3982 | 0,3980 | 0,3977 | 0,3973 |
| 0,1 | 0,3970 | 0,3965 | 0,3961 | 0,3956 | 0,3951 | 0,3945 | 0,3939 | 0,3932 | 0,3925 | 0,3918 |
| 0,2 | 0,3910 | 0,3902 | 0,3894 | 0,3885 | 0,3876 | 0,3867 | 0,3857 | 0,3847 | 0,3836 | 0,3825 |
| 0,3 | 0,3814 | 0,3802 | 0,3790 | 0,3778 | 0,3765 | 0,3752 | 0,3739 | 0,3725 | 0,3712 | 0,3697 |
| 0,4 | 0,3683 | 0,3668 | 0,3653 | 0,3637 | 0,3621 | 0,3605 | 0,3589 | 0,3572 | 0,3555 | 0,3538 |
| 0,5 | 0,3521 | 0,3503 | 0,3485 | 0,3467 | 0,3448 | 0,3429 | 0,3410 | 0,3391 | 0,3372 | 0,3352 |
| 0,6 | 0,3332 | 0,3312 | 0,3292 | 0,3271 | 0,3251 | 0,3230 | 0,3209 | 0,3187 | 0,3166 | 0,3144 |
| 0,7 | 0,3123 | 0,3101 | 0,3079 | 0,3056 | 0,3034 | 0,3011 | 0,2989 | 0,2966 | 0,2943 | 0,2920 |
| 0,8 | 0,2897 | 0,2874 | 0,2850 | 0,2827 | 0,2803 | 0,2780 | 0,2756 | 0,2732 | 0,2709 | 0,2685 |
| 0,9 | 0,2661 | 0,2637 | 0,2613 | 0,2589 | 0,2565 | 0,2541 | 0,2516 | 0,2492 | 0,2468 | 0,2444 |
| 1,0 | 0,2420 | 0,2396 | 0,2371 | 0,2347 | 0,2323 | 0,2299 | 0,2275 | 0,2251 | 0,2227 | 0,2203 |
| 1,1 | 0,2179 | 0,2155 | 0,2131 | 0,2107 | 0,2083 | 0,2059 | 0,2036 | 0,2012 | 0,1989 | 0,1965 |
| 1,2 | 0,1942 | 0,1919 | 0,1895 | 0,1872 | 0,1849 | 0,1826 | 0,1804 | 0,1781 | 0,1758 | 0,1736 |
| 1,3 | 0,1714 | 0,1691 | 0,1669 | 0,1647 | 0,1626 | 0,1604 | 0,1582 | 0,1561 | 0,1539 | 0,1518 |
| 1,4 | 0,1497 | 0,1476 | 0,1456 | 0,1435 | 0,1415 | 0,1394 | 0,1374 | 0,1354 | 0,1334 | 0,1315 |
| 1,5 | 0,1295 | 0,1276 | 0,1257 | 0,1238 | 0,1219 | 0,1200 | 0,1182 | 0,1163 | 0,1145 | 0,1127 |
| 1,6 | 0,1109 | 0,1092 | 0,1074 | 0,1057 | 0,1040 | 0,1023 | 0,1006 | 0,0989 | 0,0973 | 0,0957 |
| 1,7 | 0,0940 | 0,0925 | 0,0909 | 0,0893 | 0,0878 | 0,0863 | 0,0848 | 0,0833 | 0,0818 | 0,0804 |
| 1,8 | 0,0790 | 0,0775 | 0,0761 | 0,0748 | 0,0734 | 0,0721 | 0,0707 | 0,0694 | 0,0681 | 0,0669 |
| 1,9 | 0,0656 | 0,0644 | 0,0632 | 0,0620 | 0,0608 | 0,0596 | 0,0584 | 0,0573 | 0,0562 | 0,0551 |
| 2,0 | 0,0540 | 0,0529 | 0,0519 | 0,0508 | 0,0498 | 0,0488 | 0,0478 | 0,0468 | 0,0459 | 0,0449 |
| 2,1 | 0,0440 | 0,0431 | 0,0422 | 0,0413 | 0,0404 | 0,0396 | 0,0387 | 0,0379 | 0,0371 | 0,0363 |
| 2,2 | 0,0355 | 0,0347 | 0,0339 | 0,0332 | 0,0325 | 0,0317 | 0,0310 | 0,0303 | 0,0297 | 0,0290 |
| 2,3 | 0,0283 | 0,0277 | 0,0270 | 0,0264 | 0,0258 | 0,0252 | 0,0246 | 0,0241 | 0,0235 | 0,0229 |
| 2,4 | 0,0224 | 0,0219 | 0,0213 | 0,0208 | 0,0203 | 0,0198 | 0,0194 | 0,0189 | 0,0184 | 0,0180 |
| 2,5 | 0,0175 | 0,0171 | 0,0167 | 0,0163 | 0,0158 | 0,0154 | 0,0151 | 0,0147 | 0,0143 | 0,0139 |
| 2,6 | 0,0136 | 0,0132 | 0,0129 | 0,0126 | 0,0122 | 0,0119 | 0,0116 | 0,0113 | 0,0110 | 0,0107 |
| 2,7 | 0,0104 | 0,0101 | 0,0099 | 0,0096 | 0,0093 | 0,0091 | 0,0088 | 0,0086 | 0,0084 | 0,0081 |
| 2,8 | 0,0079 | 0,0077 | 0,0075 | 0,0073 | 0,0071 | 0,0069 | 0,0067 | 0,0065 | 0,0063 | 0,0061 |
| 2,9 | 0,0060 | 0,0058 | 0,0056 | 0,0055 | 0,0053 | 0,0051 | 0,0050 | 0,0048 | 0,0047 | 0,0046 |
| 3,0 | 0,0044 | 0,0043 | 0,0042 | 0,0040 | 0,0039 | 0,0038 | 0,0037 | 0,0036 | 0,0035 | 0,0034 |
| 3,1 | 0,0033 | 0,0032 | 0,0031 | 0,0030 | 0,0029 | 0,0028 | 0,0027 | 0,0026 | 0,0025 | 0,0025 |
| 3,2 | 0,0024 | 0,0023 | 0,0022 | 0,0022 | 0,0021 | 0,0020 | 0,0020 | 0,0019 | 0,0018 | 0,0018 |
| 3,3 | 0,0017 | 0,0017 | 0,0016 | 0,0016 | 0,0015 | 0,0015 | 0,0014 | 0,0014 | 0,0013 | 0,0013 |
| 3,4 | 0,0012 | 0,0012 | 0,0012 | 0,0011 | 0,0011 | 0,0010 | 0,0010 | 0,0010 | 0,0009 | 0,0009 |
| 3,5 | 0,0009 | 0,0008 | 0,0008 | 0,0008 | 0,0008 | 0,0007 | 0,0007 | 0,0007 | 0,0007 | 0,0006 |
| 3,6 | 0,0006 | 0,0006 | 0,0006 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0004 |
| 3,7 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0003 | 0,0003 | 0,0003 | 0,0003 |
| 3,8 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 |
| 3,9 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0001 | 0,0001 |
| 4,0 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 |
Приложение 2
Функция Лапласа 
| ||||||||||
| 0,0 | 0,0000 | 0,0040 | 0,0080 | 0,0120 | 0,0160 | 0,0199 | 0,0239 | 0,0279 | 0,0319 | 0,0359 |
| 0,1 | 0,0398 | 0,0438 | 0,0478 | 0,0517 | 0,0557 | 0,0596 | 0,0636 | 0,0675 | 0,0714 | 0,0753 |
| 0,2 | 0,0793 | 0,0832 | 0,0871 | 0,0910 | 0,0948 | 0,0987 | 0,1026 | 0,1064 | 0,1103 | 0,1141 |
| 0,3 | 0,1179 | 0,1217 | 0,1255 | 0,1293 | 0,1331 | 0,1368 | 0,1406 | 0,1443 | 0,1480 | 0,1517 |
| 0,4 | 0,1554 | 0,1591 | 0,1628 | 0,1664 | 0,1700 | 0,1736 | 0,1772 | 0,1808 | 0,1844 | 0,1879 |
| 0,5 | 0,1915 | 0,1950 | 0,1985 | 0,2019 | 0,2054 | 0,2088 | 0,2123 | 0,2157 | 0,2190 | 0,2224 |
| 0,6 | 0,2257 | 0,2291 | 0,2324 | 0,2357 | 0,2389 | 0,2422 | 0,2454 | 0,2486 | 0,2517 | 0,2549 |
| 0,7 | 0,2580 | 0,2611 | 0,2642 | 0,2673 | 0,2704 | 0,2734 | 0,2764 | 0,2794 | 0,2823 | 0,2852 |
| 0,8 | 0,2881 | 0,2910 | 0,2939 | 0,2967 | 0,2995 | 0,3023 | 0,3051 | 0,3078 | 0,3106 | 0,3133 |
| 0,9 | 0,3159 | 0,3186 | 0,3212 | 0,3238 | 0,3264 | 0,3289 | 0,3315 | 0,3340 | 0,3365 | 0,3389 |
| 1,0 | 0,3413 | 0,3438 | 0,3461 | 0,3485 | 0,3508 | 0,3531 | 0,3554 | 0,3577 | 0,3599 | 0,3621 |
| 1,1 | 0,3643 | 0,3665 | 0,3686 | 0,3708 | 0,3729 | 0,3749 | 0,3770 | 0,3790 | 0,3810 | 0,3830 |
| 1,2 | 0,3849 | 0,3869 | 0,3888 | 0,3907 | 0,3925 | 0,3944 | 0,3962 | 0,3980 | 0,3997 | 0,4015 |
| 1,3 | 0,4032 | 0,4049 | 0,4066 | 0,4082 | 0,4099 | 0,4115 | 0,4131 | 0,4147 | 0,4162 | 0,4177 |
| 1,4 | 0,4192 | 0,4207 | 0,4222 | 0,4236 | 0,4251 | 0,4265 | 0,4279 | 0,4292 | 0,4306 | 0,4319 |
| 1,5 | 0,4332 | 0,4345 | 0,4357 | 0,4370 | 0,4382 | 0,4394 | 0,4406 | 0,4418 | 0,4429 | 0,4441 |
| 1,6 | 0,4452 | 0,4463 | 0,4474 | 0,4484 | 0,4495 | 0,4505 | 0,4515 | 0,4525 | 0,4535 | 0,4545 |
| 1,7 | 0,4554 | 0,4564 | 0,4573 | 0,4582 | 0,4591 | 0,4599 | 0,4608 | 0,4616 | 0,4625 | 0,4633 |
| 1,8 | 0,4641 | 0,4649 | 0,4656 | 0,4664 | 0,4671 | 0,4678 | 0,4686 | 0,4693 | 0,4699 | 0,4706 |
| 1,9 | 0,4713 | 0,4719 | 0,4726 | 0,4732 | 0,4738 | 0,4744 | 0,4750 | 0,4756 | 0,4761 | 0,4767 |
| 2,0 | 0,4772 | 0,4778 | 0,4783 | 0,4788 | 0,4793 | 0,4798 | 0,4803 | 0,4808 | 0,4812 | 0,4817 |
| 2,1 | 0,4821 | 0,4826 | 0,4830 | 0,4834 | 0,4838 | 0,4842 | 0,4846 | 0,4850 | 0,4854 | 0,4857 |
| 2,2 | 0,4861 | 0,4864 | 0,4868 | 0,4871 | 0,4875 | 0,4878 | 0,4881 | 0,4884 | 0,4887 | 0,4890 |
| 2,3 | 0,4893 | 0,4896 | 0,4898 | 0,4901 | 0,4904 | 0,4906 | 0,4909 | 0,4911 | 0,4913 | 0,4916 |
| 2,4 | 0,4918 | 0,4920 | 0,4922 | 0,4925 | 0,4927 | 0,4929 | 0,4931 | 0,4932 | 0,4934 | 0,4936 |
| 2,5 | 0,4938 | 0,4940 | 0,4941 | 0,4943 | 0,4945 | 0,4946 | 0,4948 | 0,4949 | 0,4951 | 0,4952 |
| 2,6 | 0,4953 | 0,4955 | 0,4956 | 0,4957 | 0,4959 | 0,4960 | 0,4961 | 0,4962 | 0,4963 | 0,4964 |
| 2,7 | 0,4965 | 0,4966 | 0,4967 | 0,4968 | 0,4969 | 0,4970 | 0,4971 | 0,4972 | 0,4973 | 0,4974 |
| 2,8 | 0,4974 | 0,4975 | 0,4976 | 0,4977 | 0,4977 | 0,4978 | 0,4979 | 0,4979 | 0,4980 | 0,4981 |
| 2,9 | 0,4981 | 0,4982 | 0,4982 | 0,4983 | 0,4984 | 0,4984 | 0,4985 | 0,4985 | 0,4986 | 0,4986 |
| 3,0 | 0,4987 | 0,4987 | 0,4987 | 0,4988 | 0,4988 | 0,4989 | 0,4989 | 0,4989 | 0,4990 | 0,4990 |
| 3,1 | 0,4990 | 0,4991 | 0,4991 | 0,4991 | 0,4992 | 0,4992 | 0,4992 | 0,4992 | 0,4993 | 0,4993 |
| 3,2 | 0,4993 | 0,4993 | 0,4994 | 0,4994 | 0,4994 | 0,4994 | 0,4994 | 0,4995 | 0,4995 | 0,4995 |
| 3,3 | 0,4995 | 0,4995 | 0,4995 | 0,4996 | 0,4996 | 0,4996 | 0,4996 | 0,4996 | 0,4996 | 0,4997 |
| 3,4 | 0,4997 | 0,4997 | 0,4997 | 0,4997 | 0,4997 | 0,4997 | 0,4997 | 0,4997 | 0,4997 | 0,4998 |
| 3,5 | 0,4998 | 0,4998 | 0,4998 | 0,4998 | 0,4998 | 0,4998 | 0,4998 | 0,4998 | 0,4998 | 0,4998 |
| 3,6 | 0,4998 | 0,4998 | 0,4999 | 0,4999 | 0,4999 | 0,4999 | 0,4999 | 0,4999 | 0,4999 | 0,4999 |
| 3,7 | 0,4999 | 0,4999 | 0,4999 | 0,4999 | 0,4999 | 0,4999 | 0,4999 | 0,4999 | 0,4999 | 0,4999 |
| 3,8 | 0,4999 | 0,4999 | 0,4999 | 0,4999 | 0,4999 | 0,4999 | 0,4999 | 0,4999 | 0,4999 | 0,4999 |
| 3,9 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 |
| 4,0 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 | 0,5000 |
| Квантили нормального распределения | ||||||||||
| g | 0,8000 | 0,900 | 0,950 | 0,990 | 0,995 | 0,999 | ||||
| t g | 1,28155 | 1,64485 | 1,95996 | 2,57583 | 2,80706 | 3,29048 |
Приложения 3
| Значения t (a, k)двухстороннего критерия Стьюдента | ||||||||
| a k | 0,01 | 0,05 | 0,1 | a k | 0,01 | 0,05 | 0,1 | |
| 63,65590 | 12,70615 | 6,31375 | 2,68456 | 2,01174 | 1,67793 | |||
| 9,92499 | 4,30266 | 2,91999 | 2,68220 | 2,01063 | 1,67722 | |||
| 5,84085 | 3,18245 | 2,35336 | 2,67995 | 2,00958 | 1,67655 | |||
| 4,60408 | 2,77645 | 2,13185 | 2,67779 | 2,00856 | 1,67591 | |||
| 4,03212 | 2,57058 | 2,01505 | 2,67572 | 2,00758 | 1,67528 | |||
| 3,70743 | 2,44691 | 1,94318 | 2,67373 | 2,00665 | 1,67469 | |||
| 3,49948 | 2,36462 | 1,89458 | 2,67182 | 2,00575 | 1,67412 | |||
| 3,35538 | 2,30601 | 1,85955 | 2,66998 | 2,00488 | 1,67356 | |||
| 3,24984 | 2,26216 | 1,83311 | 2,66822 | 2,00404 | 1,67303 | |||
| 3,16926 | 2,22814 | 1,81246 | 2,66651 | 2,00324 | 1,67252 | |||
| 3,10582 | 2,20099 | 1,79588 | 2,66487 | 2,00247 | 1,67203 | |||
| 3,05454 | 2,17881 | 1,78229 | 2,66329 | 2,00172 | 1,67155 | |||
| 3,01228 | 2,16037 | 1,77093 | 2,66176 | 2,00100 | 1,67109 | |||
| 2,97685 | 2,14479 | 1,76131 | 2,66028 | 2,00030 | 1,67065 | |||
| 2,94673 | 2,13145 | 1,75305 | 2,65886 | 1,99962 | 1,67022 | |||
| 3,01228 | 2,16037 | 1,77093 | 2,65748 | 1,99897 | 1,66980 | |||
| 2,97684 | 2,14479 | 1,76131 | 2,65615 | 1,99834 | 1,66940 | |||
| 2,94671 | 2,13145 | 1,75305 | 2,65485 | 1,99773 | 1,66901 | |||
| 2,92078 | 2,11991 | 1,74588 | 2,65360 | 1,99714 | 1,66864 | |||
| 2,89823 | 2,10982 | 1,73961 | 2,65239 | 1,99656 | 1,66827 | |||
| 2,87844 | 2,10092 | 1,73406 | 2,65122 | 1,99601 | 1,66792 | |||
| 2,86093 | 2,09302 | 1,72913 | 2,65008 | 1,99547 | 1,66757 | |||
| 2,84534 | 2,08596 | 1,72472 | 2,64898 | 1,99495 | 1,66724 | |||
| 2,83136 | 2,07961 | 1,72074 | 2,64790 | 1,99444 | 1,66691 | |||
| 2,81876 | 2,07387 | 1,71714 | 2,64298 | 1,99346 | 1,66629 | |||
| 2,80734 | 2,06866 | 1,71387 | 2,63869 | 1,99006 | 1,66412 | |||
| 2,79694 | 2,06390 | 1,71088 | 2,63712 | 1,98932 | 1,66365 | |||
| 2,78744 | 2,05954 | 1,70814 | 2,63157 | 1,98667 | 1,66196 | |||
| 2,77871 | 2,05553 | 1,70562 | 2,63033 | 1,98609 | 1,66159 | |||
| 2,77068 | 2,05183 | 1,70329 | 2,62589 | 1,98397 | 1,66023 | |||
| 2,76326 | 2,04841 | 1,70113 | 2,62347 | 1,98282 | 1,65950 | |||
| 2,75639 | 2,04523 | 1,69913 | 2,62126 | 1,98177 | 1,65882 | |||
| 2,75000 | 2,04227 | 1,69726 | 2,61926 | 1,98081 | 1,65821 | |||
| 2,74404 | 2,03951 | 1,69552 | 2,61742 | 1,97993 | 1,65765 | |||
| 2,73848 | 2,03693 | 1,69389 | 2,61418 | 1,97838 | 1,65666 | |||
| 2,73328 | 2,03452 | 1,69236 | 2,61140 | 1,97705 | 1,65581 | |||
| 2,72839 | 2,03224 | 1,69092 | 2,60900 | 1,97591 | 1,65508 | |||
| 2,72381 | 2,03011 | 1,68957 | 2,60063 | 1,97190 | 1,65251 | |||
| 2,71948 | 2,02809 | 1,68830 | 2,59232 | 1,96790 | 1,64995 | |||
| 2,71541 | 2,02619 | 1,68709 | 2,58818 | 1,96591 | 1,64867 | |||
| 2,71156 | 2,02439 | 1,68595 | 2,58480 | 1,96429 | 1,64763 | |||
| 2,70791 | 2,02269 | 1,68488 | 2,58406 | 1,96393 | 1,64740 | |||
| 2,70446 | 2,02108 | 1,68385 | 2,58287 | 1,96336 | 1,64703 | |||
| 2,70118 | 2,01954 | 1,68288 | 2,58198 | 1,96294 | 1,64676 | |||
| 2,69807 | 2,01808 | 1,68195 | 2,58131 | 1,96260 | 1,64655 | |||
| 2,69510 | 2,01669 | 1,68107 | 2,58075 | 1,96234 | 1,64638 | |||
Приложения 4
| Значения c 2(a, k)критерия Пирсона | ||||||||
| a k | 0,01 | 0,05 | 0,1 | a k | 0,01 | 0,05 | 0,1 | |
| 6,635 | 3,841 | 2,706 | 72,44 | 64,00 | 59,77 | |||
| 9,210 | 5,991 | 4,605 | 73,68 | 65,17 | 60,91 | |||
| 11,345 | 7,815 | 6,251 | 74,92 | 66,34 | 62,04 | |||
| 13,277 | 9,488 | 7,779 | 76,15 | 67,50 | 63,17 | |||
| 15,09 | 11,07 | 9,236 | 77,39 | 68,67 | 64,30 | |||
| 16,81 | 12,59 | 10,645 | 78,62 | 69,83 | 65,42 | |||
| 18,48 | 14,07 | 12,02 | 79,84 | 70,99 | 66,55 | |||
| 20,09 | 15,51 | 13,36 | 81,07 | 72,15 | 67,67 | |||
| 21,67 | 16,92 | 14,68 | 82,29 | 73,31 | 68,80 | |||
| 23,21 | 18,31 | 15,987 | 83,51 | 74,47 | 69,92 | |||
| 24,72 | 19,68 | 17,28 | 84,73 | 75,62 | 71,04 | |||
| 26,22 | 21,03 | 18,55 | 85,95 | 76,78 | 72,16 | |||
| 27,69 | 22,36 | 19,81 | 87,17 | 77,93 | 73,28 | |||
| 29,14 | 23,68 | 21,06 | 88,38 | 79,08 | 74,40 | |||
| 30,58 | 25,00 | 22,31 | 89,59 | 80,23 | 75,51 | |||
| 32,00 | 26,30 | 23,54 | 90,80 | 81,38 | 76,63 | |||
| 33,41 | 27,59 | 24,77 | 92,01 | 82,53 | 77,75 | |||
| 34,81 | 28,87 | 25,99 | 93,22 | 83,68 | 78,86 | |||
| 36,19 | 30,14 | 27,20 | 94,42 | 84,82 | 79,97 | |||
| 37,57 | 31,41 | 28,41 | 95,63 | 85,96 | 81,09 | |||
| 38,93 | 32,67 | 29,62 | 96,83 | 87,11 | 82,20 | |||
| 40,29 | 33,92 | 30,81 | 98,03 | 88,25 | 83,31 | |||
| 41,64 | 35,17 | 32,01 | 99,23 | 89,39 | 84,42 | |||
| 42,98 | 36,42 | 33,20 | 100,43 | 90,53 | 85,53 | |||
| 44,31 | 37,65 | 34,38 | 101,62 | 91,67 | 86,64 | |||
| 45,64 | 38,89 | 35,56 | 102,82 | 92,81 | 87,74 | |||
| 46,96 | 40,11 | 36,74 | 104,01 | 93,95 | 88,85 | |||
| 48,28 | 41,34 | 37,92 | 105,20 | 95,08 | 89,96 | |||
| 49,59 | 42,56 | 39,09 | 106,39 | 96,22 | 91,06 | |||
| 50,89 | 43,77 | 40,26 | 107,58 | 97,35 | 92,17 | |||
| 52,19 | 44,99 | 41,42 | 108,77 | 98,48 | 93,27 | |||
| 53,49 | 46,19 | 42,58 | 109,96 | 99,62 | 94,37 | |||
| 54,78 | 47,40 | 43,75 | 111,14 | 100,75 | 95,48 | |||
| 56,06 | 48,60 | 44,90 | 112,33 | 101,88 | 96,58 | |||
| 57,34 | 49,80 | 46,06 | 124,12 | 113,15 | 107,57 | |||
| 58,62 | 51,00 | 47,21 | 135,81 | 124,34 | 118,50 | |||
| 59,89 | 52,19 | 48,36 | 148,57 | 135,48 | 129,39 | |||
| 61,16 | 53,38 | 49,51 | 158,95 | 146,57 | 140,23 | |||
| 62,43 | 54,57 | 50,66 | 170,42 | 157,61 | 151,05 | |||
| 63,69 | 55,76 | 51,81 | 181,84 | 168,61 | 161,83 | |||
| 64,95 | 56,94 | 52,95 | 189,80 | 172,58 | 122,69 | |||
| 66,21 | 58,12 | 54,09 | 201,14 | 183,31 | 131,76 | |||
| 67,46 | 59,30 | 55,23 | 212,43 | 194,02 | 140,85 | |||
| 68,71 | 60,48 | 56,37 | 223,69 | 204,70 | 149,97 | |||
| 69,96 | 61,66 | 57,51 | 234,91 | 215,37 | 159,11 | |||
| 71,20 | 62,83 | 58,64 | 246,09 | 226,02 | 168,28 | |||