РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Имеются продукты А, В, С, 1 г каждого из которых содержит следующее количество микроэлементов М и N:
| Продукты | Содержание микроэлементов, мг | |
| M | N | |
| A B C |
Стоимость 1 г продукта А составляет 14 у. е., продукта В – 15 у. е., продукта С – 18 у. е. Составьте смесь продуктов А, В и С, содержащую не менее 200 мг. Микроэлемента М и 300 мг. Микроэлемента N при условии минимальных затрат на приобретение ее составляющих.
Решение. Обозначим через x1 количество продукта А в составляемой смеси, через x2 – количество продукта В, через x3 – количество продукта С. Тогда стоимость смеси
f=14x1+15x2+18x3 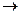 min
min
а ограничения запишем в виде

Имеем задачу на отыскание минимума. Преобразуем ее к виду, при котором требуется найти максимум целевой функции. Для этого рассмотрим функцию
f*=-f=-14x1-15x2-18x3.
Естественно, что при  имеем
имеем  . Для того чтобы в ограничениях можно было использовать знак «
. Для того чтобы в ограничениях можно было использовать знак « », умножим два первых неравенства системы на -1. в результате получим:
», умножим два первых неравенства системы на -1. в результате получим:


Запишем условие задачи в канонической форме:


Для применения симплекс-метода строим первую симплекс-таблицу (табл.2.1).
Таблица 2.1
| Базис | св | аi0 | -14 | -15 | -18 | ||||||
| x1 | x2 | x3 | x4 | x5 | |||||||
| x4 x5 | -200 -300 | -10
| -30 -10 | -30 -20 | |||||||
| Индексная cтрока | 
|
Как видно из таблицы, в индексной строке нет отрицательных элементов, однако они имеются в столбце свободных членов а 10. Для решения таких задач используются двойственный симплекс-метод. В этом случае в качестве разрешающей строки выбирают строку с наибольшим по модулю отрицательным свободным членом (в нашем примере строку x5).
Рассмотрим далее отношения элементов индексной строки к модулям соответствующих отрицательных элементов разрешающей строки. Минимальное значение среди таких отношений определит разрешающий столбец:
min(14/20, 15/10, 18/20)=min(7/10, 15/10, 9/10)=0,7
Следовательно, разрешающим будет столбец x1. Определим также разрешающий элемент. Он находится на пересечении выбранных нами строки x5 и столбца x1 и равен -20.
Переход ко второй симплекс-таблице осуществляется по тем же правилам, что и в обычном симплекс-методе: элементы разрешающей строки делим на -20 и от других строк таблицы отнимаем разрешающую строку, умноженную на некоторое число, так, чтобы в столбце с разрешающим элементом все остальные числа были равны нулю. В результате получает табл. 2.2.
Таблица 2.2
| Базис | св | аi0 | -14 | -15 | -18 | ||||
| x1 | x2 | x3 | x4 | x5 | |||||
| x4 x1 | -14 | -50 |

|
-25 1/2 | -1/2 -1/20 | ||||
| Индексная cтрока | 
| -210 | 14/20 |
В табл. 2.2 в столбце аi0 имеется отрицательный элемент, следовательно, полученный план не является оптимальным. Для его дальнейшего улучшения находим разрешающий элемент в строке с отрицательным свободным членом (в строке x4).
мin(8/25, 4/20, (14/20)/(1/2))=min(32/100, 20/100, 140/100)=0.2
Таким образом, разрешающий элемент равен -20. вновь преобразуя симплекс-таблицу по описанным выше правилам, получим табл. 2.3
Таблица 2.3
| Базис | св | аi0 | -14 | -15 | -18 | ||
| x1 | x2 | x3 | x4 | x5 | |||
| x3 x1 | -18 -14 | 2,5 12,5 |

| 5/4 -3/4 | -1/20 1/20 | 1/40 -3/40 | |
| Индексная cтрока | 
| -220 | 4/20 | 12/20 |
Так как все аi0 >0, найденное решение x1=12,5, x2=0, x3=2,5, x4=0, x5=0 является оптимальным. Значение целевой функции
 (у.е).
(у.е).
ЗАДАНИЯ
2.1. Имеются продукты А, В и С, 100 г каждого из которых содержит следующее количество микроэлементов M, N и Р.
| Продукты | Содержание микроэлементов, мг | ||
| М | N | P | |
| A B C |
Стоимость 100 г. продукта А составляет 16 у. е., продукта В – 18 у. е., продукта С – 30 у.е. Составьте смесь продуктов А, В и С, содержащую не менее 100 мг. микроэлемента М, 500 мг. микроэлемента N и 600 мг. микроэлемента P при условии минимальных затрат на приобретение ее составляющих.
Решите задачи линейного программирования 314-319
2.2. 

2.3. 

2.4. 

2.5. 

2.6. 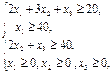

РЕШЕНИЕ ЗАДАЧ НА СОСТАВЛЕНИЕ ОПТИМАЛЬНОГО ПЛАНА
Пример решения задачи на составление оптимального плана графическим методом был рассмотрен в предыдущем практическом занятии. Серьезным недостатком графическою метода решения таких задач является невозможность его использования в том случае, когда количество переменных оказывается больше двух. Тогда применяется универсальный метод решения задач линейного программирования симплекс-метод. Его принцип заключается в последовательном переходе от одною опорного плана к другому, более близкому к оптимальному, пока задача не будет решена (т.е. будет достигнут оптимальный план).
Использованиесимплекс-метода рассмотрим на примере задачи с двумя переменными. Решим симплекс-методом задачу2 из предыдущего практического занятия и сравним полученные результаты с результатами, найденными графическимметодом. Затем рассмотрим применение симплекс-метода для решения задач, содержащих более двух переменных.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Пример 2.2.1. Решите симплекс-методом задачу 2 из предыдущего практического занятия. Напомним, что условие задачи формулируется следующим образом:
 x1+2x2
x1+2x2  140
140
3x1+x2  150
150
3x1+2x2  180
180
x1  0, x2
0, x2  0
0

Запишем условие задачи в канонической форме. Для этого введем вспомогательные переменные x3, x4, x5 так чтобы имеющиеся неравенства преобразовать в уравнения
 x1+2x2+x3=140
x1+2x2+x3=140
3x1+x2+x4=150
3x1+2x2+x5=180
x1  0, x2
0, x2  0, x3
0, x3  0, x4
0, x4  0, x5
0, x5  0
0

Положив основные переменные равными нулю (x1=0, x2=0), а вспомогательные переменные равными свободным членам в правых частях уравнений (x3 = 140, x4=150, x5 =180), получим опорное решение, соответствующее нулевым объемам выпуска продукции вида А и В. Далее следует проверить, является ли найденное опорное решение оптимальным. Если целевая функция еще не достигла максимума, то преобразуем найденное решение по определенным правилам, и будем поступать так до тех пор, пока не получим оптимальный план.
Для реализации симплекс-метода условие задачи удобно представить в виде таблицы, построенной по следующим правилам:
1) в верхнюю строку таблицы вместе с переменными выписываем коэффициенты целевой функции  (числа 2, 3, 0, 0, 0);
(числа 2, 3, 0, 0, 0);
2) далее рассматриваем базис, состоящий из вспомогательных переменных. Эти переменные записываем в первый столбец таблицы, а в следующем столбце указываем коэффициенты ciб,i = 1, 2, 3, в целевой функции f, стоящие при выбранных базисных переменных;
3) в третий столбец вносим численные значения переменных из полученного выше опорного решения (x1=0, x2=0, x3=140, x4=150, x5=180). Так как базисными являются переменные х3, х4, x5, в третьем столбце записываем числа 140, 150, 180, являющиеся правыми частями уравнений;
4) переменные, не входящие в базис, считаем равными нулю и не показываем их в таблице отдельными строками:
5) в остальные столбцы таблицы вносим коэффициенты при неизвестных из левых частей исходных уравнений. Если в уравнении соответствующая переменная отсутствует, то коэффициент при ней считаем равным нулю;
6) элементы последней строки таблицы, называемой индексной, подсчитываются по следующим формулам:
для столбца aio

для столбцов x1,x2,x3,x4,x5,
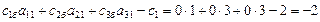




Таким образом, элементы индексной строки при построении первой симплекс-таблицы для опорного плана равны коэффициентам при неизвестных в целевой функции, взятым с противоположным знаком.
В результате выполнения описанных операций получим табл. 2.2.1.
Таблица 2.2.I
| Базис | сб | ai0 | |||||||
| x1 | х2 | x3 | x4 | x5 | |||||
| x3 | |||||||||
| x4 | |||||||||
| x5 | |||||||||
| Индексная строка | f | -2 | -3 |
Наличие отрицательных чисел в индексной строке говорит о том, что данный план не является оптимальным. Для перехода к улучшенному плану выберем столбец с наименьшим отрицательным числом в индексной строке (столбец х2, число -3). В этом столбце найдем разрешающий элемент, для которого отношение ai0/aij вычисленное для всех aij > 0, будет минимальным:
min (140/2, 150/1, 180/2) = min (70, 150, 90) = 70.
Таким образом, разрешающим элементом является число 2 (в табл. 2.2.1 оно заключено в рамку), а разрешающей строкой - первая строка.
Определив разрешающую строку, перейдем к построению новой таблицы. В ней вместо переменной x3, (соответствующей разрешающей строке) вводим в базис переменную х2 (соответствующую выбранному столбцу). Изменения вносим и во второй столбец таблицы, где указывается коэффициент в целевой функции при новой базисной переменной х2 (число 3). Все остальные элементы разрешающей строки делим на разрешающий элемент (число 2):
140/2=70, 1/2=1/2, 2/2=1, 1/2=1/2, 0/2=0, 0/2=0.
Получаем табл. 2.2.2
Таблица 2.2.2
| Базис | сб | ai0 | |||||
| x1 | х2 | x3 | x4 | x5 | |||
| x2 | 1/2 | 1/2 | |||||
| x4 | |||||||
| x5 | |||||||
| Индексная строка | f |
Остальные строки таблицы преобразуем следующим образом: вычтем из всех элементов строки соответствующие элементы новой разрешающей строки, умноженные на одно и то же число, такое, чтобы в столбце с разрешающим элементом в преобразованной строке получился нуль.
Нетрудно заметить, что для выполнения такого преобразования i-и строки от нее следует отнять новую разрешающую строку, умноженную на элемент, стоящий в i-и строке в разрешающем столбце. В нашем случае необходимо:
• от элементов строки x4 отнять соответствующие элементы новой разрешающей строки (см. табл. 2.2.2), умноженные на 1;
• от элементов строки х5 отнять соответствующие элементы новой разрешающей строки, умноженные на 2;
• от элементов индексной строки отнять соответствующие элементы новой разрешающей строки, умноженные на -3, т.е. к элементам индексной строки прибавить элементы новой разрешающей строки, умноженные на 3.
Элементы строки х4 преобразуются следующим образом:
150-70∙1=80, 3-(1/2) ∙1=5/2, 1-1∙1=0, 0-(1/2) ∙1= -1/2, 1-0∙1 = 1, 0-0∙1=0.
Элементы строки х5 преобразуются так:
180-70∙2=40, 3-(1/2) ∙2=2, 2-1∙2=0, 0-(1/2) ∙2= - 1, 0-0∙2=0, 1-0∙2=1.
Наконец, в результате преобразования элементов индексной строки имеем:
0+70∙3=210, -2+(1/2) ∙3=-1/2, -3+1∙3=0, 0 + (1/2) ∙3=3/2, 0+0∙3=0, 0+0∙3=0.
В результате всех описанных преобразований получим табл. 2.2.3:
Таблица 2.2.3
| Базис | сб | ai0 | |||||||
| x1 | х2 | x3 | x4 | x5 | |||||
| x2 | 1/2 | 1/2 | |||||||
| x4 | 5/2 | -1/2 | |||||||
| x5 | -1 | ||||||||
| Индексная строка | f | -1/2 | 3/2 |
Найденный план (х1=0, х2= 70, х3 =0, x4=80, х5=40) является улучшенным, так как в этом случае значение целевой функции 
(для первого опорного плана f =0). Однако наличие отрицательного элемента в индексной строке говорит о том, что и данный план не является оптимальным. Для его дальнейшего улучшения находим наименьшее отрицательное число в индексной строке (столбец х1 число -1/2) и определяем разрешающий элемент:
min (70/(1/2), 80/(5/2), 40/2) = min(140, 32. 20)=20.
Тогда разрешающий элемент равен 2, а разрешающей строкой является третья. Для перехода к новой таблице элементы разрешающей строки делим на разрешающий элемент 2:
40/2=20, 2/2=1, 0/2=0, -1/2=-1/2, 0/2=0, 1/2=1/2.
Для получения нуля на пересечении строки x2и столбца х1 от элементов строки х2 следует отнять элементы новой разрешающей строки, умноженные на 1/2:
70-20∙(-1/2)=60, 1/2-1∙(1/2)=0, 1-0∙(1/2)=1,
1/2+(1/2)(1/2)=3/4, 0-0∙(1/2)=0, 0-(1/2)(1/2)=-1/4.
Для получения нуля на пересечении строки х4 и столбца х1 от элементов строки х4 следует отнять элементы новой разрешающей строки, умноженные на 5/2:
80-20(5/2)=30, 5/2-1∙(5/2)=0, 0-0∙(5/2)=0,
-1/2+(1/2)(5/2)=3/4, 1-0∙(5/2)=1, 0-(1/2)(5/2)= -5/4.
Для получения нуля на пересечении индексной строки и столбца х1 от элементов индексной строки следует отнять элементы новой разрешающей строки, умноженные на -1/2 (прибавить элементы новой разрешающей строки, умноженные на 1/2):
210+20(1/2)=220, -1/2+1∙(1/2)=0, 0+0∙(1/2)=0,
3/2-(1/2)(1/2)=5/4, 0+0∙(1/2)=0, 0+(1/2)(1/2)=1/4.
В результате получим табл. 2.2.4.
Таблица2.2. 4
| Базис | сб | ai0 | |||||
| x1 | х2 | x3 | x4 | x5 | |||
| x2 | 3/4 | -1/4 | |||||
| x4 | 3/4 | -5/4 | |||||
| x1 | -1/2 | 1/2 | |||||
| Индексная строка | f | 5/4 | 1/4 |
Так как в индексной строке нет отрицательных элементов, полученный план является оптимальным, т.е. максимальная прибыль будет достигнута при плане х1 = 20, х2 = 60:

Значение переменной x4 = 30 показывает, что при таком плане неиспользованный остаток сырья вида N составит 30 т. Полученные результаты полностью соответствуют ответу, найденному графическим методом.
Пример 2. Предприятие выпускает изделия трех видов А, В и С, для производства которых требуется сырье трех видов M, N, Р в следующих количествах:
| Вид сырья | Потребности сырья, т, для производства 1 т продукции вида | ||
| A | B | C | |
| M | |||
| N | |||
| P |
Запасы сырья вида М составляют 100 т, вида N - 150 т, вида Р - 180 т. Продажа 1 т продукции вида А дает прибыль, 2 у. e., продукции вида В - 3 у.е., продукции вида С - 4 у.е. Определите, какое количество продукции вида А, В, С следует выпускать предприятию для получения максимальной прибыли.
Решение. Обозначим через х1, объем производства продукции вида А, через х2 - объем производства продукции вида В, а через х3 -объем производства продукции вида С. Тогда прибыль от реализации продукции вида А, В и С

ограничения на затраты сырья имеют вид
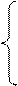 x1+2x2+x3
x1+2x2+x3  100
100
2x1+x2+2x3  150
150
x1+4x2+x3  180
180
x1  0, x2
0, x2  0, x3
0, x3  0
0
Запишем условие задачи в канонической форме. Для этого введем вспомогательные переменные х4, х5, х6так, чтобы неравенства преобразовать в уравнения
 x1+2x2+x3+x4=100
x1+2x2+x3+x4=100
2x2+x2+2x3+x5=150
x1+4x2+x3+x6=180
x1  0, x2
0, x2  0, x3
0, x3  0, x4
0, x4  0, x5
0, x5  0,x6
0,x6  0
0

Решение задачи оформим в виде табл. 2.2.5
Таблица 2.2. 5
| Базис | сб | ai0 | ||||||||
| x1 | х2 | x3 | x4 | x5 | x6 | |||||
| x4 | ||||||||||
| x5 | ||||||||||
| x6 | ||||||||||
| f | -2 | -3 | -4 | |||||||
| x4 |
| -1/2 | ||||||||
| x3 | 1/2 | 1/2 | ||||||||
| x6 | 7/2 | -1/2 | ||||||||
| f | -1 | 3/2 | ||||||||
| x2 | 50/3 | 2/3 | -1/3 | |||||||
| x3 | 200/3 | -1/3 | 2/3 | |||||||
| x6 | 140/3 | -7/3 | 2/3 | |||||||
| f | 950/3 | 2/3 | 5/3 |
В результате имеем оптимальный план (0, 50/3, 200/3, 0, 0, 140/3), при котором значение целевой функции

ЗАДАНИЯ
2.1. Для изготовления продукции трех видов А, В и С используется токарное, фрезерное и сварочное оборудование. Затраты времени на обработку одного изделия на каждом виде оборудования приведены ниже.
| Вид продукции | Затраты времени, ч | ||
| Токарное оборудование | Фрезерное оборудование | Сварочное оборудование | |
| A | |||
| B | |||
| C |
На предприятии имеется 8 токарных станков, 6 фрезерных станков и 5 сварочных аппаратов. Оборудование используется по 10 ч в день. Таким образом, в течение дня токарное оборудование может эксплуатироваться 80 ч, фрезерное - 60 ч и сварочное - 50 ч. Определите план выпуска продукции с целью получения максимальной прибыли, если прибыль от реализации продукции вида А составляет 5 у. е., продукции вида В — 3 у. е. продукции вида С - 6 у. е.
2.2. Для производства 1 т продукции каждого из трех видов А, В и С используется сырье двух видов М и N в следующих количествах:
| Вид сырья | Продукция, m | ||
| A | B | C | |
| M | |||
| N |
Запасы сырья вида M и N на предприятии составляют по 40 т каждого. Для выпуска 1 т продукции вида А требуется задействовать производственные мощности предприятия на 5 ч, для выпуска 1 т продукции вида В — на 7 ч, для выпуска 1 т продукции вида С - на 4 ч. Фонд времени использования оборудования за неделю - 70 ч. Составьте план выпуска продукции на неделю с целью получения максимальной прибыли, если прибыль от реализации 1 т продукции вида А составляет 5 у. е., продукции вида В- 3 у.е., продукции вида С-6у.е.
Решите задачи линейного программирования 1-6 симплекс – методом
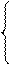 2x1+3x2+x3 2x1+3x2+x3  200
4x1+2x2+2x3 200
4x1+2x2+2x3  240
3x1+x2+x3 240
3x1+x2+x3  140
x1 140
x1  0, x2 0, x2  0, x3 0, x3  0 0
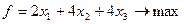
| |
 x1+2x2+x3 x1+2x2+x3  200
3x1+x2+x3 200
3x1+x2+x3  210
x1+2x2+3x3 210
x1+2x2+3x3  390
x1 390
x1  0, x2 0, x2  0, x3 0, x3  0 0
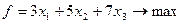
| |
 3x1+x2+3x3
3x1+x2+3x3  240
x1+2x2+x3 240
x1+2x2+x3  180
2x1+x2+4x3 180
2x1+x2+4x3  240
x1 240
x1  0, x2 0, x2  0, x3 0, x3  0 0

| |
 x1+2x2+2x3 x1+2x2+2x3  170
2x1+3x2+2x3 170
2x1+3x2+2x3  220
4x1+x2+2x3 220
4x1+x2+2x3  240
x1 240
x1  0, x2 0, x2  0, x3 0, x3  0 0

| |
 x1+x2+x3 x1+x2+x3  100
2x1+2x2+x3 100
2x1+2x2+x3  160
2x1 +x3 160
2x1 +x3  100
x1 100
x1  0, x2 0, x2  0, x3 0, x3  0 0

|