Приступая к проверке формальной математической модели, статистик обычно не знает, какому распределению соответствуют экспериментальные данные, но должен проверить, зависимы или независимы регистрируемые величины, случайны ли ошибки или же имеется систематическая ошибка, и т.д. Поэтому желательно, чтобы соответствующие статистические критерии не зависели от (неизвестного) закона распределения, а были применимы для широкого класса распределений, например, всех непрерывных. Такие критерии называются свободными от распределения.
Мы будем заниматься в ближайшее время рассмотрением трёх задач:
(I) Проверка случайности. Имеется ряд независимых наблюдений  , упорядоченных некоторым образом (например, по номеру наблюдения или по времени), так что
, упорядоченных некоторым образом (например, по номеру наблюдения или по времени), так что  ~
~  , т.е. каждое
, т.е. каждое  принадлежит к своей популяции. Проверяется гипотеза
принадлежит к своей популяции. Проверяется гипотеза  , все эти наблюдения принадлежат одной и той же генеральной совокупности, т.е. что
, все эти наблюдения принадлежат одной и той же генеральной совокупности, т.е. что  =
=  =... =
=... =  для всех
для всех  .
.
(II) Проверка независимости. Рассматривают выборку объёма 
 ,
,  ,…,
,…,  реализаций двумерной с.в.
реализаций двумерной с.в.  , имеющей ф.р.
, имеющей ф.р.  . Проверяется гипотеза
. Проверяется гипотеза  независимости
независимости  и
и  , т.е. что
, т.е. что  ; здесь
; здесь  и
и  - маргинальные ф. р. для
- маргинальные ф. р. для  и
и  .
.
(III) Проверка однородности, или задача о двух выборках. Независимым образом получены выборка  изпопуляции
изпопуляции  и вторая выборка
и вторая выборка  из популяции
из популяции  (вообще говоря,
(вообще говоря,  ). Проверяется гипотеза однородности
). Проверяется гипотеза однородности  :
:  .
.
Можно также обобщить задачу (III):
(IIIа) Задача о k выборках. Имеется  > 2 независимых выборок, каждая из которых взята из своей популяции с ф.р.
> 2 независимых выборок, каждая из которых взята из своей популяции с ф.р.  ,
,  . Проверяется гипотеза
. Проверяется гипотеза  :
:  .
.
На первый взгляд, задачи I, III и задача II касаются совершенно разных классов с.в.: задача II рассматривает многомерную с.в., а две другие задачи – одномерные. В действительности эти три задачи тесно связаны.
(а) Рассматриваем в задаче (I) двухкомпонентную величину  , приписав значениям
, приписав значениям  числа, характеризующие порядок их расположения, и рассматривая эти числа как наблюдения над с.в.
числа, характеризующие порядок их расположения, и рассматривая эти числа как наблюдения над с.в.  . Тогда (I) сводится к проверке независимости
. Тогда (I) сводится к проверке независимости  от
от  , т.е. к частному случаю (II).
, т.е. к частному случаю (II).
(б) Пусть теперь в задаче (II) мы разбили на две части область значений второй компоненты  и полагаем
и полагаем  = 1 или
= 1 или  = 2 в зависимости от того, в какую часть попадёт наблюдение
= 2 в зависимости от того, в какую часть попадёт наблюдение  . Если мы теперь будем проверять независимость
. Если мы теперь будем проверять независимость  и
и  , то задача (II) сведётся к задаче (III), так как, если
, то задача (II) сведётся к задаче (III), так как, если  верна, то
верна, то  не зависит от
не зависит от  – классификации, и если разбить
– классификации, и если разбить  две выборки в соответствии с тем, равно ли
две выборки в соответствии с тем, равно ли  единице или двум, то распределения
единице или двум, то распределения  для
для  = 1 и
= 1 и  = 2 должны быть тождественны.
= 2 должны быть тождественны.
Сначала рассмотрим решение задач (I) – (III) в важном частном случае нормального распределения данных. Аргументы для этого:
1. Ошибки измерений обычно предполагаются обусловленными действием большого числа независимых, одинаково распределённых “элементарных” погрешностей (Хаген и Бессель), представляют собой их сумму. Позднее Лаплас предположил, что в пределе эта сумма распределена нормально. Наблюдения для различных классов измерений во многих областях науки и техники подтверждают, что нормальный закон имеет место в очень большом числе случаев (но не во всех). Это положение вещей приводило к большой путанице при рассмотрении справедливости нормального закона, которая остроумно характеризована в замечании, сделанном Липманом: "Каждый уверен в справедливости закона ошибок: экспериментаторы – потому, что они думают, что это математическая теорема; а математики – потому, что они думают, что это экспериментальный факт" [приводится Пуанкаре во втором издании (1912) Poincaré "Calcul. des prob.", p. 149]. Позднее слово сказала теория: как известно по ц.п.т. (скажем, в форме Ляпунова или Линдеберга), сумма большого числа независимых с.в. таких, что вклад каждого члена в сумму стремится к 0 при неограниченном увеличении числа слагаемых, в пределе распределена по нормальному закону.
2. Многие наблюдения, распределение которых отлично от нормального, в предельных условиях хорошо описываются нормальным распределением. Например, биномиальное распределение  при
при  = const,
= const,  ® ¥ (теорема Муавра-Лапласа), распределение Пуассона
® ¥ (теорема Муавра-Лапласа), распределение Пуассона  при
при  ,
,  - распределение при
- распределение при  ® ¥, распределение Стъюдента St p при
® ¥, распределение Стъюдента St p при  ® ¥.
® ¥.
Докажем это для распределения Пуассона. Для  ~
~  имеем
имеем  ,
,  ,
,
 .
.
Рассмотрим с.в.
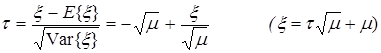 .
.
По теореме 1.3
 .
.
Разложим внутреннюю экспоненту по формуле Тейлора: 
 .
.
При  последнее выражение стремится к exp{ – t 2 / 2 }, т.е. к х.ф. нормального
последнее выражение стремится к exp{ – t 2 / 2 }, т.е. к х.ф. нормального  распределения. По второй теореме Леви (теорема 1.1 вводной лекции),
распределения. По второй теореме Леви (теорема 1.1 вводной лекции), 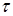
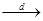
 . ÿ
. ÿ
На дом: 1)Доказать утверждение для  - распределения при
- распределения при  ® ¥. (Если
® ¥. (Если  ~
~  , то
, то  ,
,  ).
).
2) Используя выражение для ф.п.в. распределения Стьюдента c  степенями свободы ([1], стр. 198)
степенями свободы ([1], стр. 198)

и формулу Стирлинга для гамма-функции при больших значениях аргумента

(там же, стр. 190), доказать, что при  ® ¥ распределение Стъюдента St p сходится к стандартному нормальному.
® ¥ распределение Стъюдента St p сходится к стандартному нормальному.
На самом деле большинство этих асимптотик суть следствия ц.п.т., ибо, например, если  ~
~  , то можно представить её в виде
, то можно представить её в виде
 ,
,
где  – независимые одинаково распределённые (н.о.р.) с.в., причём
– независимые одинаково распределённые (н.о.р.) с.в., причём 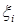 ~
~ 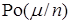 , и пусть
, и пусть  = const при
= const при  ® ¥,
® ¥,  ® ¥. Далее нужно воспользоваться воспроизводимостью распределения Пуассона и ц.п.т. Ещё легче прибегнуть к ц.п.т. в случае
® ¥. Далее нужно воспользоваться воспроизводимостью распределения Пуассона и ц.п.т. Ещё легче прибегнуть к ц.п.т. в случае  - распределения.
- распределения.
Поэтому при формировании статистики большое внимание уделялось задачам (I) – (III) для случая нормального распределения. Существуют оптимальные процедуры для их решения, которые полезно иметь в виду, осуществляя анализ на независимость, случайность или однородность. Эффективность свободных от распределения процедур можно будет сравнить с эффективностью процедур нормальной теории для совокупностей нормально распределённых данных. Наконец, мы будем пользоваться эвристическим правилом: в соответствующей статистике нормальной теории нужно заменить значения нормальных с.в. на свободные от распределения величины, и мы получим свободный от распределения критерий (правда, не гарантировано, что это будет хороший критерий).
Вспомним, что одномерное нормальное распределение  характеризуется двумя параметрами:
характеризуется двумя параметрами:  ,
,  . Сформулируем задачи (I) – (III) применительно к нормальному случаю и опишем способы их решения.
. Сформулируем задачи (I) – (III) применительно к нормальному случаю и опишем способы их решения.
(I) Случайность. В общем случае имеем ряд независимых наблюдений  , каждое из которых представляет свою популяцию:
, каждое из которых представляет свою популяцию:  ~
~  . Проверяется гипотеза
. Проверяется гипотеза  :
:  ,
,  . Обычно альтернативой является альтернатива тренда
. Обычно альтернативой является альтернатива тренда 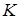 : наблюдения
: наблюдения  независимы, нормальны,
независимы, нормальны,  , но
, но
 (тренд вверх),
(тренд вверх),
или
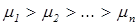 (тренд вниз).
(тренд вниз).
Общая дисперсия  обычно неизвестна (при известной
обычно неизвестна (при известной  статистика
статистика
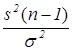 ~
~  , и для проверки
, и для проверки  против
против 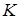 используется правый хвост
используется правый хвост  - распределения, так что для заданного размера критерия
- распределения, так что для заданного размера критерия 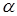 критическое множество
критическое множество  есть
есть
 , где
, где  ),
),
и  также неизвестно. Тогда
также неизвестно. Тогда  можно оценить двумя способами, если
можно оценить двумя способами, если  верна – через выборочную дисперсию
верна – через выборочную дисперсию
 (1)
(1)
(это несмещённая оценка  , её эффективность равна
, её эффективность равна  ([1], стр. 399)), и через сумму квадратов разностей соседних значений:
([1], стр. 399)), и через сумму квадратов разностей соседних значений:
 . (2)
. (2)
Оценка (2) – несмещённая и состоятельная, если  верна. Действительно,
верна. Действительно,

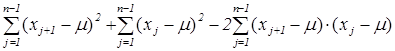 ,
,
и тогда  , так как
, так как  – н.о.р.
– н.о.р.  с.в. Отсюда
с.в. Отсюда  =
=  – оценка
– оценка  несмещённая.
несмещённая.
Покажем, что  – состоятельная оценка. Для этого рассмотрим разность 2
– состоятельная оценка. Для этого рассмотрим разность 2  - 2
- 2  и покажем, что эта с.в. сходится по вероятности к 0, если
и покажем, что эта с.в. сходится по вероятности к 0, если  верна: 2
верна: 2  - 2
- 2  =
=  - 2
- 2  =
=
=  =
= 
 (3)
(3)
Первое и второе слагаемые – однотипные, так что рассмотрим, например, второе слагаемое в (3). Его можно записать как
 =
=
 (4)
(4)
С.в.  имеет дисперсию
имеет дисперсию  , так что
, так что  =
=  . Отсюда для любого заданного малого
. Отсюда для любого заданного малого  по неравенству Чебышёва (если h - с.в. с м.о. E { h } = m и дисперсией Var{ h }, и пусть e > 0 – произвольное число, то P {| h - m| ³ e } £
по неравенству Чебышёва (если h - с.в. с м.о. E { h } = m и дисперсией Var{ h }, и пусть e > 0 – произвольное число, то P {| h - m| ³ e } £  ), получим
), получим
 ,
,
т.е. вероятность этого события стремится к 0 при  .
.
Первое слагаемое в (4)  –
–  сходится к 0 по вероятности (в книге [1], стр. 212, доказано, что если
сходится к 0 по вероятности (в книге [1], стр. 212, доказано, что если  – выборка из распределения с дисперсией
– выборка из распределения с дисперсией  и четвёртым центральным моментом
и четвёртым центральным моментом  , то
, то  , а
, а  =
=  , откуда, применив неравенство Чебышёва, доказываем состоятельность
, откуда, применив неравенство Чебышёва, доказываем состоятельность  . Кстати, для нормального распределения
. Кстати, для нормального распределения  =
=  ).
).
Итак, мы показали, что  сходится к 0 по вероятности; рассмотрение первой суммы в (3) аналогично. Третье слагаемое в (3) – удвоенная оценка
сходится к 0 по вероятности; рассмотрение первой суммы в (3) аналогично. Третье слагаемое в (3) – удвоенная оценка  автоковариации
автоковариации  с лагом 1 (если
с лагом 1 (если  – стационарный случайный процесс c дискретным параметром t, то E { x t} = m при всех t, а функция лага
– стационарный случайный процесс c дискретным параметром t, то E { x t} = m при всех t, а функция лага  ,
, 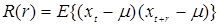 называется автоковариационной функцией; её оценкой по совокупности (
называется автоковариационной функцией; её оценкой по совокупности ( ) является
) является
 =
= 
– см. [1], стр. 517, 522), и так как с.в.  и
и  статистически независимы, она стремится к 0 по вероятности, когда
статистически независимы, она стремится к 0 по вероятности, когда  ® ¥ (см. формулу (5.3.25) книги Priestley, M.B. (1981) Spectral Analysis and Time Series, Vol.1: Univariate Series. Academic Press, Inc., London: при
® ¥ (см. формулу (5.3.25) книги Priestley, M.B. (1981) Spectral Analysis and Time Series, Vol.1: Univariate Series. Academic Press, Inc., London: при  >> 1
>> 1
 ; (5.3.25)
; (5.3.25)
результат получен Бартлеттом в 1946 г. См. также аналогичную формулу (48.7) в книге М.Кендалла, А.Стьюарта «Многомерный статистический анализ и временные ряды». М.: Наука, 1976. В нашем случае речь идёт о стационарном гауссовом процессе с некоррелированными данными, для которого 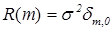 .Поэтому сумма в правой части (5.3.25) конечна, и третье слагаемое в (3) сходится к 0 по вероятности в силу неравенства Чебышёва), что завершает доказательство состоятельности
.Поэтому сумма в правой части (5.3.25) конечна, и третье слагаемое в (3) сходится к 0 по вероятности в силу неравенства Чебышёва), что завершает доказательство состоятельности  .
.
Пусть верна  . Тогда статистика отношения оценок дисперсии (1) и (2)
. Тогда статистика отношения оценок дисперсии (1) и (2)
 (5)
(5)
с большой вероятностью близка к 1, ибо оценки в числителе и знаменателе (5) несмещённые и состоятельные. Действительно, ещё в XIX веке Хельмерт доказал, что если верна Н, то E { q } = 1, Var { q } =  Если же верна альтернатива тренда
Если же верна альтернатива тренда 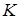 , то знаменатель
, то знаменатель  больше числителя, так что для выбранного размера критерия
больше числителя, так что для выбранного размера критерия 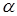 малые значения
малые значения
 <
< 
свидетельствуют в пользу 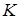 (тренда) против
(тренда) против  . Это критерий Аббе (см. Большев Л.Н., Смирнов Н.В. “Таблицы математической статистики”. М.: Наука, 1965). Процентные точки
. Это критерий Аббе (см. Большев Л.Н., Смирнов Н.В. “Таблицы математической статистики”. М.: Наука, 1965). Процентные точки  для
для  £ 60 имеются в указанной книге Большева и Смирнова, а также в [13]. При больших
£ 60 имеются в указанной книге Большева и Смирнова, а также в [13]. При больших  вспомогательная с.в.
вспомогательная с.в.  =
=  имеет стандартное нормальное
имеет стандартное нормальное  , и
, и  отвергается при заданном размере критерия
отвергается при заданном размере критерия 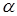 , если
, если  <
< 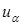 (т.е.
(т.е. 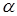 -квантили
-квантили  ). Критерий Аббе есть в отечественном пакете анализа временных рядов «Эвриста». В зарубежных статистических пакетах, мне доступных, я не нашёл критерия Аббе, но в STATGRAPHICS и STATISTICA есть тесно связанная с q статистика Дарбина-Уотсона (Durbin-Watson)
). Критерий Аббе есть в отечественном пакете анализа временных рядов «Эвриста». В зарубежных статистических пакетах, мне доступных, я не нашёл критерия Аббе, но в STATGRAPHICS и STATISTICA есть тесно связанная с q статистика Дарбина-Уотсона (Durbin-Watson)  , и часто пользуются ей (о ней можно прочитать в книге Дж.Себера “Линейный регрессионный анализ”, п. 6.6.2, и Дрейпер Н., Смит Г. “Прикладной регрессионный анализ”, т.1 (1986), с.209-213).
, и часто пользуются ей (о ней можно прочитать в книге Дж.Себера “Линейный регрессионный анализ”, п. 6.6.2, и Дрейпер Н., Смит Г. “Прикладной регрессионный анализ”, т.1 (1986), с.209-213).
(II) Независимость. Есть наблюдения  ,
,  ,…,
,…,  над двумерной с.в.
над двумерной с.в.  ~
~ 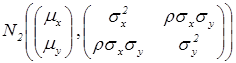 . Проверяется гипотеза независимости компонент
. Проверяется гипотеза независимости компонент  и
и  . Далее (см. [7], гл.6) будет доказано, что необходимым и достаточным условием независимости
. Далее (см. [7], гл.6) будет доказано, что необходимым и достаточным условием независимости  - мерных нормальных с.в. (
- мерных нормальных с.в. ( ³ 2) является их некоррелированность (см. также теорему 6.0 темы «Нормальная регрессия»).
³ 2) является их некоррелированность (см. также теорему 6.0 темы «Нормальная регрессия»).
Действительно, в нашем случае двумерной с.в.
 ~
~ 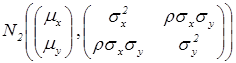 (где
(где  ,
,  ,
,  ,
,  ,
,  = corr{
= corr{  ,
,  }), её х.ф. равна
}), её х.ф. равна
 .
.
Если  , то
, то

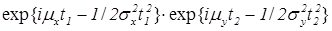 =
=
=  ,
,
т.е. характеристическая функция двумерной с.в. представляется в виде произведения х.ф. одномерных с.в.; а, по теореме 1.2, это необходимое и достаточное условие независимости компонент. ÿ
Итак, проверяется гипотеза  :
:  . Её альтернативы
. Её альтернативы  ,
,  или двухсторонняя альтернатива
или двухсторонняя альтернатива  . В гл.5 моей книги [7] показано, что для параметров
. В гл.5 моей книги [7] показано, что для параметров  и
и  двумерного нормального распределения статистики
двумерного нормального распределения статистики  ,
,  ,
,  и
и  являются МП–оценками (оценками максимального правдоподобия). Здесь
являются МП–оценками (оценками максимального правдоподобия). Здесь  – выборочный коэффициент корреляции
– выборочный коэффициент корреляции
 , (6)
, (6)
а, например,  – оценка для
– оценка для  , равная
, равная
 =
=  . (7)
. (7)
Статистика ОП для проверки  :
:  равна
равна  , так что большие значения
, так что большие значения  являются критическими против альтернативы
являются критическими против альтернативы  , отрицательные
, отрицательные  » -1 – критические при альтернативе
» -1 – критические при альтернативе  , а его модуль – против альтернативы
, а его модуль – против альтернативы 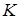 (мы докажем это позднее, в корреляционном анализе). Тогда же будет доказано, что в частном случае
(мы докажем это позднее, в корреляционном анализе). Тогда же будет доказано, что в частном случае  (т.е. когда
(т.е. когда  верна), статистика
верна), статистика
 (8)
(8)
имеет распределение Стъюдента Stn – 2. Поэтому нетрудно вычислить процентные точки критерия для проверки  , основанного на
, основанного на  . Более того, если
. Более того, если  отвергается, имеются номограммы доверительных зон для
отвергается, имеются номограммы доверительных зон для  , если
, если  для некоторых стандартных размеров критерия, вроде
для некоторых стандартных размеров критерия, вроде 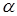 = 0.05 (см. [2], Приложение Ш), так что есть возможность построить интервальные оценки
= 0.05 (см. [2], Приложение Ш), так что есть возможность построить интервальные оценки  . Во всех мне известных статистических пакетах, и даже в Maple, Mathematica и Excel имеется процедура вычисления
. Во всех мне известных статистических пакетах, и даже в Maple, Mathematica и Excel имеется процедура вычисления  и квантилей распределения Стьюдента.
и квантилей распределения Стьюдента.
(3) Однородность (two-sample problem). Пусть рассматриваются две с.в.  и
и  , и в результате
, и в результате  наблюдений с.в.
наблюдений с.в.  получена выборка
получена выборка  ~
~  , а
, а  наблюдений за с.в.
наблюдений за с.в.  дают вторую независимую выборку
дают вторую независимую выборку  из популяции
из популяции  ; вообще говоря,
; вообще говоря,  . Проверяется гипотеза
. Проверяется гипотеза  :
:  в частном случае нормального распределения, т.е.
в частном случае нормального распределения, т.е.  :
: 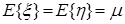 ,
, 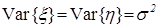 . Эта задача рассматривается в теоретическом плане в [4], стр. 227 – 233, а с точки зрения практических применений – в [2], стр. 273 и след. Возможные альтернативы:
. Эта задача рассматривается в теоретическом плане в [4], стр. 227 – 233, а с точки зрения практических применений – в [2], стр. 273 и след. Возможные альтернативы:
 :
: 
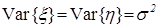 ;
;
 :
: 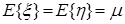 ,
,  ;
;
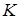 :
: 
 .
.
Мы уже отмечали, что согласно общему курсу статистики выборочное среднее и выборочная дисперсия являются достаточными статистиками для параметров  и
и  . Тогда и критерии для проверки
. Тогда и критерии для проверки  являются функциями этих статистик. Эти критерии суть ([2], [4]):
являются функциями этих статистик. Эти критерии суть ([2], [4]):
(а) для  : Могут быть две ситуации: общая дисперсия
: Могут быть две ситуации: общая дисперсия  известна, либо
известна, либо  неизвестна. Рассмотрим сначала более лёгкую, с известной
неизвестна. Рассмотрим сначала более лёгкую, с известной  . Поскольку МП-оценкой для
. Поскольку МП-оценкой для  является выборочное среднее, то представляется разумным выбрать в качестве статистики для проверки
является выборочное среднее, то представляется разумным выбрать в качестве статистики для проверки  против
против  разность выборочных средних
разность выборочных средних  , имеющую нормальное распределение
, имеющую нормальное распределение  , если
, если  верна; распределение tmp следует из статистической независимости
верна; распределение tmp следует из статистической независимости  ,
,  и из теоремы Фишера. К сожалению, эта статистика неудобна для практического применения, так как её критические точки зависят от объёмов выборок
и из теоремы Фишера. К сожалению, эта статистика неудобна для практического применения, так как её критические точки зависят от объёмов выборок  и
и  , и от значения стандартного отклонения
, и от значения стандартного отклонения  . Но можно масштабировать tmp и рассмотреть статистику
. Но можно масштабировать tmp и рассмотреть статистику  вида
вида
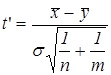 , (9)
, (9)
 ~
~  , если
, если  известна (распределение с.в.
известна (распределение с.в.  следует из усиленной воспроизводимости нормального распределения). Если же
следует из усиленной воспроизводимости нормального распределения). Если же  неизвестна, то, по теореме Фишера, для выборки
неизвестна, то, по теореме Фишера, для выборки  с.в.
с.в.
 ~
~ 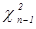 .
.
Точно так же для выборки  с.в.
с.в.
 ~
~  .
.
Наши выборки не зависят друг от друга, и поэтому, в силу воспроизводимости Хи- квадрат распределения, с.в.
 ~
~  .
.
Вспоминаем, что если с.в. h ~  , то E { h } = k. Поэтому
, то E { h } = k. Поэтому
E {  } = n + m – 2,
} = n + m – 2,
и  оценивают выборочной дисперсией для объединённой выборки
оценивают выборочной дисперсией для объединённой выборки
 . (10)
. (10)
Статистика
 ~
~  , (11)
, (11)
где 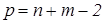 . По той же теореме с.в.
. По той же теореме с.в.  и
и  статистически независимы. Следовательно, статистика
статистически независимы. Следовательно, статистика
 (12)
(12)
имеет распределение Стъюдента St p. Для проверки  против
против  при заданном размере критерия
при заданном размере критерия 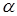 критическим множеством является
критическим множеством является
 (13)
(13)
где процентная точка  – решение уравнения
– решение уравнения
 , (14)
, (14)
а  – ф.п.в. для St p . Другими словами, используется двусторонний критерий (13), так как альтернативой
– ф.п.в. для St p . Другими словами, используется двусторонний критерий (13), так как альтернативой  служит
служит  . К сожалению, это «наивное» рассмотрение ничего не говорит о мощности критерия (12), (13). Поэтому далее мы рассмотрим применение критерия ОП для задачи с одной и с двумя выборками.
. К сожалению, это «наивное» рассмотрение ничего не говорит о мощности критерия (12), (13). Поэтому далее мы рассмотрим применение критерия ОП для задачи с одной и с двумя выборками.
Лемма 2.1. Пусть  – среднее арифметическое для
– среднее арифметическое для  . Для произвольного
. Для произвольного  ,
,  справедливо тождество:
справедливо тождество:
 . (15)
. (15)
Доказательство. 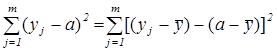 =
=
=  =
=
=  . ÿ
. ÿ
Чтобы получить статистику  из критерия ОП, рассмотрим сначала более простую задачу: имеется выборка
из критерия ОП, рассмотрим сначала более простую задачу: имеется выборка  =
=  ~
~ 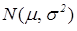 . Проверяется гипотеза
. Проверяется гипотеза  :
:  против альтернативы
против альтернативы 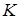 :
:  произвольно. Функция правдоподобия (ФП) есть
произвольно. Функция правдоподобия (ФП) есть
 , (16)
, (16)
а её логарифм
 . (16¢)
. (16¢)
Введём с.в.
 . (17)
. (17)
Пользуясь леммой 2.1, можно записать логарифмическую ФП (16¢) в виде:
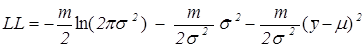 .
.
Максимизация  по
по  и
и  равносильна минимизации функции
равносильна минимизации функции
g ( ,
,  ) = ln(
) = ln( ) +
) +  +
+  .
.
Прежде всего, последний член,  , всегда ³ 0, и он обращается в 0 при
, всегда ³ 0, и он обращается в 0 при  =
=  . Отсюда МП-оценка
. Отсюда МП-оценка
 . (18)
. (18)
Осталось рассмотреть выражение ln( ) +
) +  как функцию
как функцию  ; оно эквивалентно ln
; оно эквивалентно ln  +
+  = - ln t + t (мы положили t =
= - ln t + t (мы положили t =  ). Но при t > 0 функция t - ln t ³ 1, причём равенство наступает лишь при t = 1. Отсюда
). Но при t > 0 функция t - ln t ³ 1, причём равенство наступает лишь при t = 1. Отсюда
 s 2МП =
s 2МП =  . (19)
. (19)
Таким образом, что МП-оценки параметров  и
и  (18) и (19) реализуют глобальный максимум ФП (16). Значение логарифма ФП в точке безусловного максимума равно
(18) и (19) реализуют глобальный максимум ФП (16). Значение логарифма ФП в точке безусловного максимума равно  .
.
Если же максимизировать  в предположении, что
в предположении, что  верна, т.е.
верна, т.е.  , то МП–оценкой дисперсии является
, то МП–оценкой дисперсии является
 , (20)
, (20)
(На дом: показать, что  - не просто стационарная точка, а точка условного максимума ФП (16)!), и для неё
- не просто стационарная точка, а точка условного максимума ФП (16)!), и для неё
 (m0,
(m0,  ) = const - m / 2 ln
) = const - m / 2 ln  – m/2.
– m/2.
Тогда логарифм отношения правдоподобия (ОП) равен
ln l ( ) =
) =  (m 0 ,
(m 0 ,  ;
;  ) –
) –  (
( ,
,  ;
;  ) =
) = 
и тогда  отвергается, если
отвергается, если  /
/