Прежде чем решать задачу ЛП симплекс-методом ее необходимо привести к каноническому виду:
 (1.7)
(1.7)

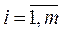 (1.8)
(1.8)

 (1.9)
(1.9)

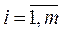
Для этого в случае необходимости задача (1.1) поиска минимума сводится к задаче на поиск максимума (1.7) путем изменения знаков коэффициентов Сj
 ;
;
Неравенства (1.2) преобразуются в строгие равенства путем введения дополнительных неотрицательных переменных; условия неотрицательности (1.3) распространяются на все переменные путем введения подстановок.
Пример. Дана задача ЛП в общем виде:



Приведем ее к каноническому виду. Условие неотрицательности не распространяется на переменную х2. Поэтому введем подстановку: х2 = х5 – х4, где  .
.
Тогда



Изменим вид экстремума на максимум:

Изменим неравенства на строгие равенства путем введения дополнительных неотрицательных переменных. Тогда



Основные понятия и определения. Исходная задача (1.7), (1.8), (1.9) может быть представлена в векторной форме:

x1Р1+x2Р2+…+xnPn=P0

С=(c1, c2 … cn); X=(x1,x2 … xn); P1,P2…Pn, P0 – m-мерные вектор-столбцы.
Вектор X=(x1,x2 … xn) называется опорным планом задачи ЛП, если он удовлетворяет ограничениям (1.8); (1.9) и содержит m отличных от нуля положительных компонент. Остальные (n-m) элементов опорного плана равны нулю. Алгоритм симплекс-метода предполагает переход от одного опорного плана к другому с увеличением при этом значения целевой функции.
В некоторых случаях исходный опорный план можно легко определить. Это происходит тогда, когда среди векторов Pj  имеется m единичных. В этом случае соответствующие единичным векторам переменные в опорном плане будут отличны от нуля. Они называются базисными. Остальные переменные равны нулю; они называются свободными.
имеется m единичных. В этом случае соответствующие единичным векторам переменные в опорном плане будут отличны от нуля. Они называются базисными. Остальные переменные равны нулю; они называются свободными.
Симплекс-преобразования продолжаются до тех пор, пока среди чисел 
 не будет отрицательных.
не будет отрицательных.
Исходная симплекс-таблица в общем случае имеет вид
| i | Базис | Сб | P0 | C1 | C2 | … | Cm | Cm+1 | … | Cn |
| P1 | P2 | … | Pm | Pm+1 | … | Pn | ||||
| P1 | C1 | b1 | … | a1m+1 | … | a1n | ||||
| P1 | C2 | b2 | … | a2m+1 | … | a2n | ||||
| … | … | … | … | … | … | … | … | … | … | … |
| m | Pm | Cm | bm | … | amm+1 | … | amn | |||
| M+1 | F0 | … | Δm+1 | … | Δn |
В столбце Сб записываются коэффициенты целевой функции с теми же индексами, что и векторы базиса.
В столбце Р0 записываются положительные компоненты исходного опорного плана, в нем же в результате вычислений получают положительные компоненты оптимального плана. В столбцах Р1…Рn записаны коэффициенты ограничений при неизвестных.
В (m+1)-й строке: F0 – текущее значение целевой функции; в столбцах Pj  записаны числа
записаны числа  .
.
Алгоритм решения.
1. Задачу ЛП приводят к каноническому виду и находят исходный опорный план.
2. Составляют исходную симплекс-таблицу.
3. Определяют, имеется ли хотя бы одно отрицательное число Δj в (m+1)-й строке. Если нет, то найденный опорный план оптимален.
4. Находят наименьшее отрицательное Δj и соответствующий столбец обозначают как разрешающий. Если в разрешающем столбце среди чисел aij нет положительных, то целевая функция не ограничена сверху, а задача ЛП не имеет решения.
5. Находят отношения bi к положительным aij разрешающего столбца. Минимальное из этих отношений определяет разрешающую строку.
6. На пересечении разрешающих строки и столбца определяют разрешающий элемент.
7. Все элементы разрешающей строки делят на разрешающий элемент.
8. Все элементы разрешающего столбца (кроме разрешающего элемента) заменяют нулями.
9. Остальные элементы таблицы рассчитываются по правилу прямоугольника и фиксируется введение в базис новой переменной. При этом разрешающая строка определяет переменную, которая исключается из базиса, а разрешающий столбец – переменную, которая вводится в базис.
10. Переходят к пункту 3.
Правило прямоугольника
| a1 | … | A2 |  p. строка p. строка
| ||
| … | … | ||||
| a3 | … | А4 | |||
 p. столбец
p. столбец
|

Пример. Решить задачу ЛП:
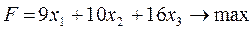


1. Представим задачу в каноническом виде:

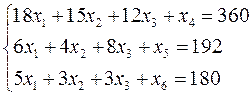


Найдем опорный план X=(0,0,0,360,192,180). Т.о. базисные переменные x4, x5, x6; свободные – x1, x2, x3.
2. Составим исходную симплекс-таблицу:
| I | Базис | Сб | P0 | bi/aij | |||||||
| P1 | P2 | P3 | P4 | P5 | P6 | ||||||
| P4 | 360/12=30 | ||||||||||
| P5 | 192/8=24 |  p.стр p.стр
| |||||||||
| P6 | 180/3=60 | ||||||||||
| -9 | –10 | –16 | |||||||||
 p.ст.
p.ст.
|
Δ1= 0·18 + 0·6 + 0·5 – 9 = – 9
Δ2= 0·15 + 0·4 + 0·3 – 10 = – 10
Δ3= 0·12 + 0·8 + 0·3 – 16 = – 16
Δ4= 0·1 + 0·0 + 0·0 – 0 = 0
Δ5= 0·0 + 0·1 + 0·0 – 0 = 0
Δ6= 0·0 + 0·0 + 0·1 – 0 = 0
3. Найденный опорный план X=(0,0,0,360,192,180) не оптимален, т.к. Δ1, Δ2, Δ3 – отрицательны.
4.  – разрешающий столбец
– разрешающий столбец
5. 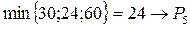 – разрешающая строка
– разрешающая строка
6. а23 = 8 – разрешающий элемент.
7, 8, 9, 10 Строим новую симплекс-таблицу по приведенному выше алгоритму, вводя в базис P3 вместо P5.
| I | Базис | Сб | P0 | bi/aij | |||||||
| P1 | P2 | P3 | P4 | P5 | P6 | ||||||
| P4 | –3/2 | 72/9=8 |  p.стр p.стр
| ||||||||
| P3 | 6/8 | 1/2 | 1/8 | 24:1/2 = 48 | |||||||
| P6 | 11/4 | 3/2 | –3/8 | 108: 3/2=72 | |||||||
| –2 | |||||||||||
 p.ст.
p.ст.
|
Полученный опорный план X=(0,0,24,72,0,108) так же не оптимален, т.к. Δ2= – 2 < 0. Поэтому по алгоритму симплекс-метода переходим к новому опорному плану, вводя в базис P2 вместо P4.
| i | Базис | Сб | P0 | bi/aij | ||||||
| P1 | P2 | P3 | P4 | P5 | P6 | |||||
| P2 | 1/9 | –1/6 | ||||||||
| P3 | 1/4 | –1/8 | 5/24 | |||||||
| P6 | 5/4 | –1/6 | –1/8 | |||||||
| 2/9 | 5/3 |
Этот опорный план X*=(0; 8; 20; 0; 0; 96) оптимален, т.к. все Δj  неотрицательны.
неотрицательны.
Максимальное значение функции на оптимальном решении равно:
Fmax = 0·9 + 8·10 + 20·16 + 0·0 + 0·0 + 0·96 = 400
Решение общей задачи ЛП: x1*= 0; x2* = 8; x3* = 20; Fmax= 400.
Индивидуальные задания. Решить задачу ЛП симплексным методом. Варианты заданий взять из индивидуальных заданий пункта 1.1.
1.3. Метод искусственного базиса.
В общем случае после приведения задачи ЛП к каноническому виду непосредственно записать опорный план не удается, т.к. среди векторов Pj  . нет m единичных. В этом случае задача ЛП решается методом искусственного базиса.
. нет m единичных. В этом случае задача ЛП решается методом искусственного базиса.
Постановка задачи. Требуется найти максимум функции
 (1.10)
(1.10)
При условиях
 (1.11)
(1.11)




m<n,
но среди векторов Pj 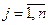 нет m единичных.
нет m единичных.
Определение. Задача, состоящая в определении максимума функции
 (1.12)
(1.12)
при условиях
 (1.13)
(1.13)




называется расширенной по отношению к исходной задаче (1.10), (1.11).
Здесь M некоторые большие положительные числа, значения которых не задаются.
Расширенная задача (1.12), (1.13) имеет опорный план:

Переменные xn+1, xn+2 … xn+m называются искусственными, а система единичных векторов Pn+1, Pn+2 … Pn+m образует искусственный базис.
Если в оптимальном плане  расширенной задачи (1.12), (1.13) значения искусственных переменных равны нулю, то
расширенной задачи (1.12), (1.13) значения искусственных переменных равны нулю, то 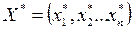 – есть оптимальный план исходной задачи (1.10), (1.11).
– есть оптимальный план исходной задачи (1.10), (1.11).
Поэтому процесс решения задачи ЛП (1.10), (1.11) включает следующие этапы:
1. Для исходной задачи составляют расширенную задачу вида (1.12), (1.13).
2. Находят опорный план расширенной задачи.
3. С помощью вычислений симплекс-метода исключают искусственные вектора из базиса. В результате находят опорный план исходной задачи. Если искусственные переменные исключить из базиса не удается, то задача ЛП неразрешима.
4. Используя найденный опорный план исходной задачи (1.10), (1.11), либо находят симплекс-методом ее оптимальный план, либо устанавливают ее неразрешимость
Пример. Найти минимум функции 
при условиях:



Представим эту задачу в каноническом виде:




Для образования базиса необходимо три единичных вектора, т.к. m = 3. Но среди векторов Pj 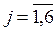 :
:




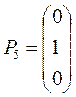

есть только два единичных – P4 и P5. Поэтому составим расширенную задачу, введя искусственную переменную x7 в целевую функцию и в третье ограничение:




Расширенная задача имеет опорный план X=(0;0;0;24;22;0;10), определяемый базисом P4, P5, P7.
Составим исходную таблицу:
| i | Базис | Сб | P0 | –3 | -M | bi/aij | ||||||
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | ||||||
| P4 | –2 | |||||||||||
| P5 | 22/4 | |||||||||||
| P7 | –M | –1 | –1 | 10/2 |  p.стр. p.стр.
| |||||||
| –8 | ||||||||||||
| –10 | –1 | –2 | ||||||||||
 р.ст.
р.ст.
|
F=1·24+0·22+(–M) ·10 = 24 – 10M
Δ1= 2·1 + 1·0 + 1·(–M) – 2 = 0 – M
Δ2= 1·1 + 2·0 + 2(–M)–(–3) =4 + M
Δ3= (–2)·1 + 4·0 + 2(–M)–6=–8–2M
Δ4= 1·1 + 0·0 + 0·(–M) – 1 = 0
Δ5= 0·1 + 0·0 + 0·(–M) – 0 = 0
Δ6= 0·1 + 0·0 + (–1)·(–M) – 0=M
Δ7= 0·1 + 0·0 + 1·(–M) – (–M)=0
При этом в (m+2)-й строке записываем коэффициенты при М. В начале проверяем условие  для последней (пятой) строки. Здесь есть отрицательные числа:
для последней (пятой) строки. Здесь есть отрицательные числа:  и
и  .
.
Переходим к новому опорному плану по алгоритму симплекс-метода. Для этого исключим вектор P7 из базиса, а вектор P3 введем вместо него. В дальнейшем искусственный вектор P7 не имеет смысла вводить в базис, поэтому столбец P7 исключаем из таблицы.
Так как все искусственные векторы исключены из базиса то нет смысла включать в таблицу и (m+2)-ю (пятую для нашей задачи) строку.
Поэтому новая таблица имеет четыре строки и шесть столбцов:
| I | Базис | Сб | P0 | –3 | bi/aij | ||||||
| P1 | P2 | P3 | P4 | P5 | P6 | ||||||
| P4 | –1 | ||||||||||
| P5 | –1 | 2/2 |  p.стр. p.стр.
| ||||||||
| P3 | 1/2 | –1/2 | –1/2 | ||||||||
| -4 | |||||||||||
 р.ст.
р.ст.
|
Полученное опорное решение Х=(0;0;5;34;2;0) не является оптимальным; т.к. Δ6<0.
Дальше итерационный процесс ведется по (m+1)-й строке до получения оптимального решения или установления неразрешимости задачи.
Вводим в базис P6 вместо P5 и переходим к новой таблице:
| I | Базис | Сб | P0 | –3 | bi/aij | |||||
| P1 | P2 | P3 | P4 | P5 | P6 | |||||
| P4 | 5/2 | 1/2 | ||||||||
| P6 | –1/2 | 1/2 | ||||||||
| P3 | 11/2 | ¼ | 1/2 | 1/4 | ||||||
Т.к. все 
 , то полученный опорный план
, то полученный опорный план  – оптимальный.
– оптимальный.  .
. 
Индивидуальные задания. Решить задачу ЛП методом искусственного базиса. Варианты заданий взять из индивидуальных заданий пункта 1.1.