Применение его позволяет получить хорошие результаты при расчете подпятников. При расчете цилиндрических подшипников с увеличением эксцентриситета существенно увеличиваются расхождения между теоретическими и экспериментальными значениями. Это вызвано тем, что метод не учитывает окружные перетечки газа из одного сектора в другой, которые при больших эксцентриситетах весьма значительны.
В МВТУ им. Н.Э. Баумана предложен метод расчета однорядных подшипников с учетом окружных перетечек [133, 135, 136, 137]. Для учета перетечек по окружности применяются экспериментальные коэффициенты.
В Казанском химико-технологическом институте предложена методика расчета опор с наддувом паров хладагентов [111, 112].
Окружные перетечки газа учитываются изменением условной ширины сектора в зависимости от его расположения и эксцентриситета.
Аналитический метод расчета газостатических подшипников с питающими щелями предложен в работах [219, 220,].
Большой вклад в развитие теории газовой смазки внесли работы, выполненные на кафедре гидроаэродинамики Ленинградского политехнического института. В работах [54, 57, 59, 60, 62, 212, 213, 215, 224, 225,] приведено несколько аналитических методов решения отдельных задач газовой смазки.
В связи с развитием вычислительной техники и повсеместным внедрением ЭВМ наиболее перспективными для расчета газовых подшипников являются численные методы. К настоящему времени накоплен большой опыт численного решения уравнения для распределения давлений в газодинамических подшипниках c недеформируемыми поверхностями. В работах [14, 92, 93, 94, 160] уравнение распределения давлений преобразуется в эквивалентные уравнения в конечных разностях и решается итерациями до удовлетворения граничным условиям. Достоверных и доступных пользователю методик расчёта подшипников с упруго деформируемыми поверхностями нет.
В случае газостатических подшипников задача значительно усложняется, так как приходится рассматривать многосвязную область. Количество граничных условий увеличивается. При этом граничные условия на кромке питателей, как правило, не линейны и являются неизвестными. Численным методам расчета подшипников с газовой смазкой посвящены работы [5, 7, 63, 73, 74, 75, 76, 77, 125, 240, 237, 253, 254, 271, 272, 277, 315]. Работа [74] имеет общий характер. В ней анализируются различные методы вычислительной математики, которые можно применить для решения задач газовой смазки. В работе [93] рассматривается конечно-разностный метод решения линейных эллиптических уравнений с линейными граничными условиями.
В работе [7] приводится метод численного решения с учетом вращения цапфы для однорядного газостатического подшипника с наддувом воздуха, компенсированного дроссельными отверстиями. В работе указывается, что вращение шипа не оказывает существенного влияния на распределение давления в смазочном слое, а следовательно, и на несущую способность подшипника. В работе [63] излагаются результаты численного решения задачи газовой смазки гладкого сферического подшипника, компенсированного дроссельными отверстиями. В этих работах принимается аппроксимация дискретного наддува линией наддува. Функция изоэнтропийного истечения из сопла аппроксимируется соотношением, предложенным Прандтлем для воздуха.
Мэджумдар (В.С.Majumdar) [301, 302, 303, 304, 305] представил теоретическое решение для радиальных подшипников с газовой смазкой с учетом как осевого, так и окружного потока смазки. Он числено решил уравнение Рейнольдса для ламинарного изотермического вязкого слоя, когда толщина слоя является функцией одной координаты
(1. 15)
Развертка поверхности подшипника показана на рис.1.24.
При использовании квадратной сетки уравнение (1.15) сводится к пятиточечному конечно-разностному уравнению, если
(1.16)
, (1.17)
где 
– давление в любом узле сетки, 
Распределение давления 
можно получить из уравнения (1.17) с учетом значений давлений на границах. В качестве граничных значений давления Мэджумдар принимал атмосферное давление на торцах подшипника и давления за отверстиями подачи газа в зазор (давления на кромке питателей), которые предварительно определял следующим образом.
Для одной из линий питания (например, для линии 1) принимается произвольное значение давления, а давление для других линий считаются равными атмосферному. Затем из уравнения (1.17), которое решается итерационным методом, находится распределение давления, удовлетворяющие указанным произвольным значениям давления на границах.
Z
q 
pD
3 q3 линия питания №3
q2
2 линия питания №2
q2
q1
L/8 1 линия питания №1
L/4 X
3/8L
L/2
Рис.1.24. Развёртка подшипника
После этого записываются уравнения для определения массовых расходов в осевом и окружном направлениях для всех других линий питания.
Массовый расход в осевом направлении для линии q (рис.1) определяется выражением
(1.18)
а расход в окружном направлении от линии q до линии m равен
, (1.19)
где,
I1= Р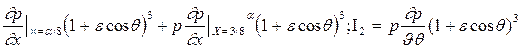 
Здесь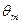 
– угол положения линии питания m, n – число линий питания Эти массовые расходы Мэджумдар выражает в безразмерной форме
и 
(1.20)
Общий расход, обеспечиваемый линией q определяется как
(1.21)
Массовый расход через два отверстия на любой линии q будет равен
при 
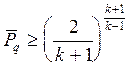
(1.22)
при 
,
где 
– безразмерное давление на кромке питателя для любой линии наддува, Fо – площадь ограничительного отверстия, ap – коэффициент расхода.
При установившемся режиме расход через питатель равен расходу смазки, вытекающей из подшипника. Соотношения, дающие расход для n линий (где n-четное число), составляют систему уравнений:
----------------------------------------------------------
---------------------------------------------------------- (1.23)
С учётом выражений (1.20), (1.22) из уравнений (1.23) можно получить 
+ 
----------------------------------------------------------------------
----------------------------------------------------------------------
+ 
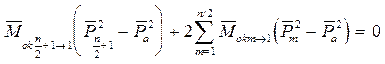
(1.24)
где d= 
Для первые члены уравнений (1.24) примут вид
, а все другие члены останутся теми же.
Система (1.24) включает (n/2+1) нелинейных уравнений относительно 
. Эти уравнения решаются числено методом Ньютона-Рафсона для различных значений L/D,n, 
.
После того, как давления за отверстиями будут найдены, конечно-разностное уравнение (1.17) решается итерационным методом с учётом действительных граничных условий.
Несущая способность подшипника
Расход смазки
Результаты расчётов по этому методу довольно хорошо согласуются с результатами экспериментов для подвесов, при отсутствии вращения и перекосов шипа в подшипнике. Но метод не пригоден для расчёта подшипников быстроходных турбомашин, для подшипников, в которых смазочный слой изменяется по нескольким координатам. Кроме того, при принятом относительно большом шаге сетки вызывает сомнение точность определения давления за отверстиями наддува.
Численный метод расчета подшипников с наддувом газа предложен в Польше сотрудниками Лодзинского политехнического института [288, 289, 290, 291, 292, 294, 295]. Уравнение нестационарного течения газа в смазочном зазоре упорного подшипника записано в цилиндрических координатах в размерном виде
(1.25)
Это уравнение справедливо для участков смазочного слоя, не содержащих источников газа. Принятая геометрия системы координат показана на рис.1.25
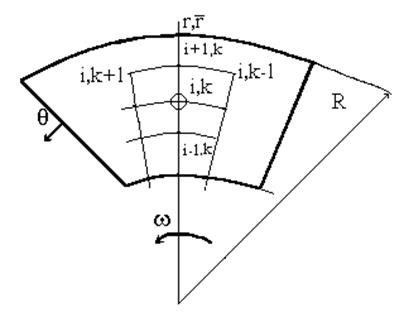
Рис.1.25. Фрагмент упорного подшипника
Для смазочного слоя в котором на некотором бесконечно малом участке площадью dr×rdq (Dr×rdq), рис.1.25) подводится газ, уравнение Рейнольдса в безразмерной форме записывается в виде:
, (1.26)
где M – расход газа через один питатель
Уравнение Рейнольдса для цилиндрического опорного подшипника с наддувом при параллельных осях цапфы и подшипника
(1.27)
где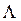 
= 
, с – радиальный зазор в подшипнике при концентричном положении шипа.
Для области интегрирования, не включающий источника газа, правая часть уравнения (1.26) будет равна нулю.
Так как расход газа через питатель неизвестен, при расчётах используется относительный расход газа через питатель.
где 
– критический расход газа через питатель при изоэнтропийном истечении газа.
После введения величины 
в формулу (1.26) и преобразований, правая сторона этого уравнения принимает вид
или 
(1.28)
где 
– коэффициент расхода, dc – диаметр питателя, ro – радиус кармана
где 
– критическая скорость звука в, 
– скорость звука в газе при давлении Ps. r0 – радиус питания или кармана в зависимом от типа наддува.
Первая из формул (1.28) предназначена для подшипников с внутренней компенсацией, вторая для систем наддува с постоянной компенсацией дроссельным отверстием.
Значения Nm для каждого питателя в начале проектирования неизвестны и вычисляются исходя из баланса расходов через отверстия и смазочный слой. При этом учитываются результаты экспериментов [63, 64, 268, 270, 276, 299, 317].
Расход газа через питатель с постоянной компенсацией определяется по формуле
(1.29)
Коэффициент расхода ap определяется по формуле /55/.
Относительный расход газа через питатель Nm есть функция от 
и k.
,
при 
и Nm=0,85 при 
При подстановке значения М из уравнения(1.29) в правую часть уравнения (1.27), можно правую часть уравнения (1.27) записать в виде
Расход газа через питатель с внутренней компенсацией определяется по формуле:
Исходя из модели, представленной в работе [292] переменное давлениеР1 на кромке питателя
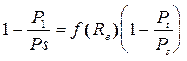или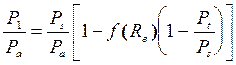 
, (1.30)
где Рt – условное давление, соответствующие расширению без потерь в отверстии сечением 2proh,
Число Рейнольдса:
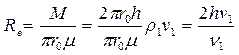
где 
, 
, 
– плотность, скорость и кинематическая вязкость соответственно, r0 – здесь радиус питателя.
Через относительный расход Nm газа через питатель, Число Рейнольдса записываются в виде
Поправочный коэффициент f(Rе) вычисляется в соответствии /54/ по формулам:
при Rе £ 200 f(Rе) = 0,16+0,0002Rе
2000 < Rе < 400 f(Rе) = 0,685+0,155y-0,19y 
Re ³ 4000 f(Re) = 0,715
у =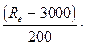 
Максимальное значение Nm ограничивается значением 0,85. Правая часть уравнения (1.29) записывается в виде:
В обоих случаях наддува считают, что в районе питателя изменения давления в смазочном слое, обусловленные конвекцией, значительно превышают изменения давления, вызванные движением цапфы и изменениями зазора во времени. В этом случае при 
уравнения (1.26) и (1.27) приводятся к уравнению Лапласа
Решением его является функция
с граничным условием P = P1 на кромке питателя.
При переходе к безразмерному давлению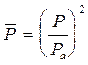 
и конечным разностям получены следующие зависимости
(1.31)
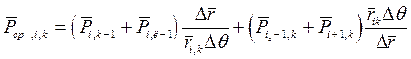
FK1= 
Система уравнений (1.30) и (1.31) служит для определения двух неизвестных 
После решения этой системы в основное уравнение (1.26) подставляется относительный расход газа Nm. А вычисленное здесь давление P1 может быть не равно давлению получаемому из решения основного уравнения. Основное уравнение описывает только баланс масс, выраженный через Nm.
Для упорного подшипника при параллельных поверхностях цапфы и подшипника основное уравнение записывается следующим образом:
Граничные условия: атмосферное давление на внутреннем и наружном диаметрах подшипника и условие периодичности.
При решении этого уравнения предлагается, что первоначальное распределение 
представляется упрощенно в трапециевидной форме. В процессе численного решения нестационарной задачи производная по времени приравнивается к нулю, а затем находится решение стационарной задачи, как предел ряда нестационарных решений. Метод реализации таких алгоритмов представлен в [262].
Полученные результаты хорошо совпадают с результатами экспериментальных исследований в определенных диапазонах геометрических и режимных параметров подшипников.
Все результаты расчетов представлены в зависимости от безразмерных параметров подобия, полученных авторами исходя из геометрического подобия подшипников и расчетных уравнений с граничными условиями, записанных в безразмерной форме. Но метод расчета очень громоздок. Не бесспорной является аргументация авторов при отборе параметров подобия. Так они утверждают [291], что не следует принимать во внимание соотношение c/R, потому что оно значительно меньше единицы, но учитывают соотношение dc/D, которое в ряде случаев имеет тот же порядок.
Интересная задача – нахождение оптимальной конфигурации смазочного слоя - рассматривается в работах [17, 18, 19, 20, 21, 33, 127, 300].
В работах [318, 319, 320, 321] сравниваются по точности различные методы определения несущей способности и жесткости подшипников с наддувом газа с экспериментальными данными (рис.1.26) и делается вывод, что результаты, полученные по анализируемым авторам методам и экспериментальные значения существенно расходятся и ни одному из методов нельзя отдать предпочтение. Поэтому при проектировании подшипников с газовой смазкой для различных турбомашин без проверки полагаться на имеющиеся в литературе методы расчета и рекомендации по проектированию полностью нельзя.
Изложенный краткий обзор проведенных исследований подшипников с газовой смазкой позволяет сделать ряд выводов. В связи с повсеместным внедрением в практику электронных вычислительных машин, самыми перспек-
тивными становятся численные методы решения задач газовой смазки. Численные методы имеет минимум упрощающих допущений, малый объем алгебраических выражений и вследствие этого могут обеспечить большую точность расчета. Точность и быстрота получения результатов зависят от применяемого алгоритма и составленной программы расчета. Существующие работы, посвященные численным методам расчета подшипников с газовой смазкой громоздки и не доведены до инженерной методики расчёта, а численные методы расчёта подшипников с упругодеформируемыми поверхностями, основанные на совместном решении уравнения распределения давления в смазочном слое и уравнений прогибов лепестков недоступны. В связи с конфиденциальным характером многих разработок подшипников с газовой смазкой, алгоритмы, программы расчета, характеристик подшипников и рекомендации по проектированию целесообразно разрабатывать самостоятельно и полученные результаты проверять экспериментально.
При использовании пара в качестве смазки возможно возникновение вибрации ротора, не зависящей от его вращения, и эрозия цапф и втулок подшипников [130, 236, 273, 314].
Смазка паром является эффективной для турбомашин, где пар является рабочим веществом. Такие турбомашины обычно имеют значительную массу роторов, поэтому необходимо применять двухрядные подшипники, которые обладают большей грузоподъемностью по сравнению с однорядными. Ввиду возможности возникновения вибрации ротора перспективно применение подшипников с внутренней компенсацией, которые являются более устойчивыми по сравнению с подшипниками, компенсированными дроссельными отверстиями.
2. РАСЧЕТ ПОДШИПНИКОВ С ГАЗОВОЙ СМАЗКОЙ
2.1. Общие уравнения газовой смазки
С теоретической точки зрения смазка газом сводится к изучению движения газа, т.е. вязкой сжимаемой жидкости, в тонком слое переменной толщины (рис. 2.1). Уравнения газовой смазки выводятся из общих уравнений движения вязких сжимаемых жидкостей. Эти уравнения являются следствием физических свойств газов и законов механики и термодинамики.
y
v2r
v2q h
o v1r r
v1q
 |
Рис. 2.1. Расположение осей координат на двух поверхностях,
ограничивающих смазочный слой
Собственно уравнения движения являются записью уравнений механики сплошных сред для случая ньютоновских жидкостей. Они выражают динамическое равновесие элементарной частицы жидкости, т.е. равновесие действующих на частицу сил инерции, массовых сил и напряжений. Эти уравнения, известные в гидромеханике под названием уравнений Навье-Стокса, имеют вид [80]:
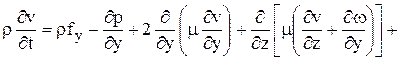
(2.1)
Здесь 
– компоненты внешних сил, отнесённые к единице массы.
Уравнения движения существенно упрощаются, если учесть допущения классической теории смазки:
общепринятое допущение в задачах динамики вязкого газа о пренебрежимой малости массовых сил [80], так как масса частицы газа очень мала, т.е.
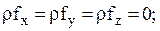
силами инерции смазки можно пренебречь [144];
при движении газа в тонком слое компоненты u, v, w скорости 
частицы газа – величины разного порядка, так как скорость v, направленная по нормали к поверхности подшипника, значительно меньше (в 
раз) компонентов u и w.
В результате уравнения движения газа в смазочном слое можно записать следующим образом [80]:
,
(2.2)
В цилиндрических координатах эти уравнения движения будут иметь вид
. (2.3)
Если вязкость 
считать постоянной по толщине слоя h, то
(2.4)
Из этих уравнений легко можно найти распределение скоростей u и ω в смазочном слое, если известны граничные условия. При определении граничных условий для скоростей газа в смазочном слое подшипника полагают, что в точках поверхностей, ограничивающих смазочный слой (рис. 2.1), скорости частиц газа и поверхности одинаковы по величине и направлению, т. е.
при y = 0 
при 
(2.5)
Проинтегрируем по y первое из уравнений движения (2.4):
Интегрируя второй раз получим
u = 
Постоянные интегрирования определяются из граничных условий (2.5)
при y = 0 u = v 
; 
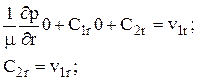
при y = h 
В результате получим распределение скорости u по толщине смазочного слоя
(2.6)