Часто приходится составлять из конечного числа элементов различные комбинации и производить подсчет числа всех возможных комбинаций, составленных по некоторому правилу. Такие задачи называются комбинаторными, а раздел математики, занимающийся их решением, называется комбинаторикой.
Правило суммы: если некоторый объект A можно выбрать m способами, а объект B – k способами, причем любой способ выбора объекта A отличен от любого способа выбора B, то выбор «A или B » можно сделать m + k способами.
Правило произведения: пусть объект A можно выбрать m способами, а после каждого такого выбора другой объект B можно выбрать (независимо от объекта A) k способами, то пару объектов A и B можно выбрать mk способами.
Множество называется упорядоченным, если каждому элементу этого множества поставлено в соответствие некоторое натуральное число (номер элемента) от 1 до n, где n – число элементов множества, так что различным элементам соответствуют различные числа.
Различные упорядоченные множества, которые отличаются лишь порядком элементов (т. е. могут быть получены из того же самого множества), называются перестановками. Число возможных перестановок из n элементов вычисляют по формуле
(1)
(читается «n -факториал»).
Конечные упорядоченные подмножества данного множества называются размещениями данного множества.
Число упорядоченных k -элементных подмножеств множества, состоящего из n элементов, т. е. число размещений изnпоk обозначают 
и вычисляют по формуле
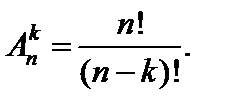(2)
Произвольное k -элементное подмножество n -элементного множества называется сочетаниемиз n элементов по k. Число сочетаний из n элементов по k обозначается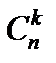 
и вычисляется по формуле
З а м е ч а н и е. Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае множества с повторениями вычисляются по другим формулам.
Если среди n элементов есть n 1 элементов одного вида, n 2 элементов другого вида и т. д., то число перестановок с повторениями определяется формулой
где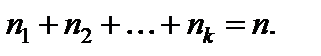 
Число размещений по k элементов с повторениями из n элементов равно nk, т. е.
Число сочетаний с повторениями из n элементов по k элементов равно числу сочетаний без повторений из n + k –1 элементов по k элементов, т. е.
Пример. Определить, сколько двузначных чисел можно записать в десятичной системе счисления.
Решение. Число десятков двузначного числа может принимать одно из девяти значений: 1, 2, 3, 4, 5, 6, 7, 8, 9. Число единиц может принимать одно из десяти значений: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Всего получим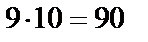 
двузначных чисел.
Пример. Определить, сколькими различными способами могут разместиться на скамейке 6 человек.
Решение. Согласно формуле (31.2) при n = 6, находим
Пример. Определить,сколькими способами можно выбрать четырех человек на четыре различные должности из девяти кандидатов на эти должности.
Решение. Воспользуемся формулой (31.3). При n = 9, k = 4 получаем
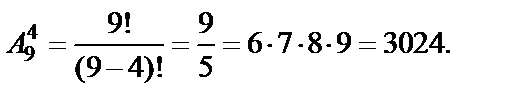
Пример. В девятом классе 35 учащихся. Из них нужно выбрать четыре делегата на конференцию. Определить, сколько имеется возможностей такого выбора.
Решение.
Пример. Определить, сколькими способами можно поставить на книжной полке три экземпляра учебника по алгебре, два экземпляра учебника по физике и один экземпляр учебника по белорусскому языку.
Решение.
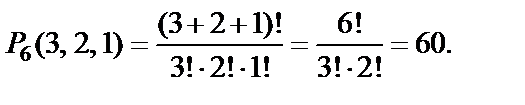
Пример. Сколько разных пятизначных чисел можно составить из цифр 0, 2, если одна и та же цифра может повторяться несколько раз?
Решение. Из цифр 0, 2 можем получить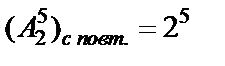 
пятизначных чисел. Но числа, записанные пятью цифрами, первая из которых нуль, не являются пятизначными.
Их столько, сколько четырехзначных чисел можно составить из цифр 0, 2 при повторении цифр, т. е. 
Поэтому ответ: 
Пример. Сколько различных списков (отличающихся порядком фамилий) можно составить из 7 различных фамилий?
Решение. Р 7 = 7! = 2·3·4·5·6·7 = 5040.
Пример. Сколько возможно различных вариантов пьедестала почета (первое, второе, третье места), если в соревнованиях принимают участие 10 человек?
Решение.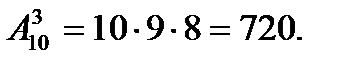 
Пример. В отборочных соревнованиях принимают участие 10 человек, из которых в финал выходят трое. Сколько может быть различных троек финалистов?
Решение. В отличие от предыдущего примера, здесь не важен порядок финалистов, следовательно, ищем число сочетаний из 10 по 3:
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. Что называется упорядоченным множеством?
2. Как определяется перестановка?
3. Что такое размещение?
4. Чем отличается размещение и сочетание?
5. Какая формула вычисления числа размещений с повторениями?
6. Назовите формулы вычисления числа перестановок, сочетаний, размещений без повторений.
Домашнее задание: [4], §1.1-1.4, 1.5-1.8, №1-5