Тема 11. Производные высших порядков. Монотонность и локальный экстремум функции
Если  есть производная от функции
есть производная от функции  , то производная от
, то производная от  называется второй производной, или производной второго порядка и обозначается
называется второй производной, или производной второго порядка и обозначается  , или
, или  , или
, или  .
.
Аналогично определяются производные любого порядка:производная третьего порядка  ; производная n-го порядка:
; производная n-го порядка:
 .
.
Для произведения двух функций можно получить производную любого n-го порядка, пользуясь формулой Лейбница:

Пример:
1)

Вторая производная от неявной функции
 -уравнение определяет
-уравнение определяет 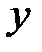 , как неявную функцию от х.
, как неявную функцию от х.
а) определим 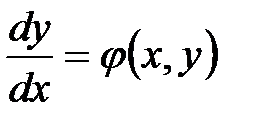 ;
;
б) продифференцируем по х левую и правую части равенства  ,
,
причем, дифференцируя функцию  по переменной х, помним, что
по переменной х, помним, что  есть функция от х:
есть функция от х:

 ;
;
в) заменяя  через
через  , получим:
, получим:  и т.д.
и т.д.
Пример:

Производные от функций, заданных параметрически


Пример:
Найти  если
если  .
.

Наибольшее и наименьшее значение функций на промежутке
Всюду далее функция f (x) определена на рассматриваемых промежутках.
Теорема 1 (достаточное условие монотонности). Дифференцируемая на (a, b) функция возрастает (убывает) на этом интервале тогда и только тогда, когда 


Точка х 0 называется точкой локального максимума (минимума) функции f (x), если существует некоторая окрестность точки  такая, что для всех x из этой окрестности выполняется неравенство
такая, что для всех x из этой окрестности выполняется неравенство 

Значение  называется локальным максимумом (минимумом) функции.
называется локальным максимумом (минимумом) функции.
Точки максимума или минимума функции называются точками экстремума (локального). Максимум и минимум называются экстремумом функции.
Теорема 2 (необходимое условие существования экстремума функции). Если в точке  функция f (x) достигает экстремума, то ее производная в этой точке равна нулю или не существует.
функция f (x) достигает экстремума, то ее производная в этой точке равна нулю или не существует.
Те точки из области определения функции f (x), в которых производная функции f (x) обращается в нуль или не существует, называют критическими. Исследование функции на экстремум начинается с нахождения критических точек. Однако не в каждой критической точке существует экстремум. Для того чтобы определить точки экстремума, используют достаточные условия (признаки экстремума).
Теорема 3 (первый признак экстремума функции). Пусть  – критическая точка непрерывной функции f (x). Если в некоторой окрестности точки
– критическая точка непрерывной функции f (x). Если в некоторой окрестности точки  выполняется условие
выполняется условие

то  – точка локального максимума;
– точка локального максимума;
если выполняется условие

то  – точка локального минимума.
– точка локального минимума.
Если производная  имеет один и тот же знак в левой и правой полуокрестности точки
имеет один и тот же знак в левой и правой полуокрестности точки  то
то  не является точкой экстремума.
не является точкой экстремума.
Теорема 4 (второй признак экстремума функции). Пусть  – критическая точка дважды дифференцируемой функции f (x). Тогда
– критическая точка дважды дифференцируемой функции f (x). Тогда  является точкой локального минимума функции f (x), если
является точкой локального минимума функции f (x), если  и точкой локального максимума, если
и точкой локального максимума, если 
Теорема 5 (третий признак экстремума функции). Пусть f (x) – n раз непрерывно дифференцируемая в критической точке  функция и
функция и 
 Тогда:
Тогда:
1) если n – четное и  то
то  – точка локального максимума;
– точка локального максимума;
2) если n – четное и  то
то  – точка локального минимума;
– точка локального минимума;
3) если n – нечетное, то  не является точкой локального экстремума.
не является точкой локального экстремума.
З а м е ч а н и е 1.При исследовании функции и построении ее графика целесообразно использовать первый признак экстремума, так как одновременно получаем возможность исследования функции на монотонность.
Точка  называется точкой глобального максимума (минимума) функции f (x) на некотором промежутке, если для любой точки x из этого промежутка выполняется неравенство
называется точкой глобального максимума (минимума) функции f (x) на некотором промежутке, если для любой точки x из этого промежутка выполняется неравенство 

Точки глобального максимума и минимума называются точками глобального экстремума. Значения функции в этих точках называются соответственно глобальным максимумом (наибольшим значением) и глобальным минимумом (наименьшим значением).
Пример 1. Найти экстремумы функции 
Решение. Подозрительными на экстремумы точками будут те, в которых производная функции либо равна нулю, либо не существует.
Найдем производную функции:

Она определена для любого 
Приравняем производную к нулю:
 значит,
значит,  Решая это уравнение, получим
Решая это уравнение, получим  Областью определения функции является числовая прямая.
Областью определения функции является числовая прямая.
Исследуем функцию на экстремум в этих точках тремя способами.
1-й способ. Воспользовавшись теоремой 3, исследуем поведение функции на промежутках 


Для этого определим знак производной, т. е. выражения  Очевидно, что для всякого
Очевидно, что для всякого  выполняется неравенство
выполняется неравенство  Поэтому знак выражения
Поэтому знак выражения  зависит от знака квадратичного выражения
зависит от знака квадратичного выражения  (рис. 17.4).
(рис. 17.4).
| + |
| – |
| + |
| x |

|

|

|
Рис. 17.4
Так как при «переходе» через точку с абсциссой  производная
производная  меняет знак с «+» на «–», то, согласно теореме 1, в этой точке функция достигает максимума.
меняет знак с «+» на «–», то, согласно теореме 1, в этой точке функция достигает максимума.
При «переходе» через точку  производная
производная  меняет знак с «–» на «+». Поэтому в данной точке функция достигает минимума.
меняет знак с «–» на «+». Поэтому в данной точке функция достигает минимума.
2-й способ. Воспользуясь теоремой 4, вычислим вторую производную функции:

Вычислим ее значение в критических точках  и
и 

Согласно теореме 4, в точке  функция достигает максимума.
функция достигает максимума.

Согласно теореме 4 в точке  функция достигает минимума.
функция достигает минимума.
3-й способ. Воспользуемся теоремой 5. Так как производная первого порядка в точке  равна нулю, а производная второго (четного) порядка в этой точке меньше нуля, то, согласно теореме 5,
равна нулю, а производная второго (четного) порядка в этой точке меньше нуля, то, согласно теореме 5,  – точка локального максимума. В точке
– точка локального максимума. В точке  производная первого порядка также равна нулю, а производная второго (четного) порядка больше нуля. Следовательно, точка
производная первого порядка также равна нулю, а производная второго (четного) порядка больше нуля. Следовательно, точка  – точка локального минимума.
– точка локального минимума.
Вычислим максимум и минимум функции.
Максимум функции равен значению функции в точке 

Итак, локальный максимум функции равен 
Вычислим значение функции в точке 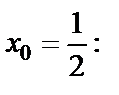

Итак, локальный минимум функции равен 
Пример 2. Найти наибольшее и наименьшее значения функции  на отрезке [– 2, 2].
на отрезке [– 2, 2].
Решение. Найдем точки, которые будут подозрительными на экстремум. Для этого вычислим производную функции


Производная существует во всех точках  Найдем критические точки. Полагаем
Найдем критические точки. Полагаем  т. е.
т. е.  Получаем
Получаем  Обе точки
Обе точки  и
и 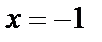 принадлежат интервалу (– 2, 2). Поэтому, будем искать значение функции в этих точках и на концах отрезка. Вычисляем:
принадлежат интервалу (– 2, 2). Поэтому, будем искать значение функции в этих точках и на концах отрезка. Вычисляем:




Выбрав среди полученных значений наибольшее и наименьшее, получаем:

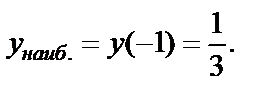
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. Как определяется производная второго порядка?
2. Как находится вторая производная от неявной функции?
3. Как находятся производные от функций, заданных параметрически?
4. Сформулируйте достаточное условие монотонности.
5. Что такое экстремум функции?
6. Сформулируйте первый признок экстремума функции.
7. Сформулируйте второй признок экстремума функции.
8. Сформулируйте третий признок экстремума функции.
9. Что такое глобальный экстремум?
Домашнее задание: [1], ч.2, §11.1, 11.2, ч.3 §17.4