Тема 22. Комплексные числа и операции над ними
Число вида 
(1)
где а, 
i – мнимая единица, определяемая равенством 
называется комплексным числом.
Число а называется действительной частью комплексного числа z и обозначается 
b называется мнимой частью комплексного числа z и обозначается 
Запись комплексного числа в виде (1.12) называется алгебраической формой комплексного числа.
Если 
то комплексное число называется чисто мнимым; при 
получается действительное число.
Множество всех комплексных чисел обозначают С. Имеет место: R Ì C.
В прямоугольной декартовой системе координат комплексное число 
изображается точкой M с абсциссой a и ординатой b (рис. 1). Между множеством всех точек координатной плоскости и множеством всех комплексных чисел существует взаимно-однозначное соответствие. Координатная плоскость называется комплексной плоскостью. Ось абсцисс называется действительной осью, ось ординат – мнимой осью.
| M (a, b) |
| a |
| x |
| y |
| b |
Рис. 1
Два комплексных числа 
и 
называются равными, если соответственно равны их действительные и мнимые части:
Если 
то число 
называется сопряженным числу z и обозначается 
Сопряженные числа в системе координат изображаются точками, симметричными относительно оси 
Действия над комплексными числами в алгебраической форме
Пусть 
тогда:
(2)
(3)
(4)
Формулы (2)–(4) показывают, что операции сложения, вычитания и умножения выполняются аналогично таким же действиям над многочленами (с учетом 
при умножении).
Для нахождения частного комплексных чисел 
и 
сначала числитель и знаменатель дроби 
умножают на сопряженное знаменателю число 
а затем производят остальные действия:
|
|
(5)
Свойства комплексно-сопряженных чисел:
1) 
2) 
3) 
4) 
5) 
6) 
Пример 1. Найти 
и 
если
1) 
2) 
3) 
Решение. 1) Так как 
то 
2) Поскольку 
3) Запишем число в стандартном виде: 
Поэтому 
Пример 2. Даны комплексные числа 
и 
Найти:
1) 
2) 
3) 
4) 
Решение. 1) 
2) 
3) Перемножим числа 
и 
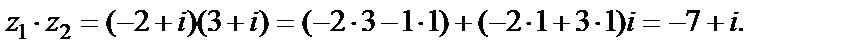
4) Для нахождения частного 
умножим числитель и знаменатель дроби на 
(т. е. на число, сопряженное знаменателю). Тогда получим
Пример 3. Найти число, сопряженное числу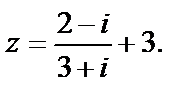 
Решение. Умножив числитель и знаменатель дроби на 
получим
Тогда 
Пример 4. Вычислить 
для n Î N.
Решение. При вычислении используем, что, согласно определению, 
Тогда
Очевидно, что значения степени повторяются циклически:
где 
.
Пример 5. Найти множество точек, для которых 
Решение. Поскольку 
точки искомого множества лежат на прямой 
параллельной мнимой оси (рис. 1).
| х |
| у |
| Re z = 5 |
Рис. 1
Пример 6. Показать на координатной плоскости множество всех точек, которые находятся на расстоянии, равном 3, от точки 
Решение. Пусть 
– одна из искомых точек. На плоскости ей соответствует точка с координатами 
Точке 
соответствует точка плоскости с координатами 
В качестве решения задачи подходят все точки, для которых
т. е. 
Полученному уравнению соответствует множество точек окружности с центром в точке 
и радиусом 3 (рис. 2).
Рис. 2
Тригонометрическая и показательная формы комплексного числа
Комплексное число 
в прямоугольной декартовой системе координат Оху изображается точкой М (рис. 3).
|
|
| M |
| a |
| x |
| y |
| b |
| j |
Рис. 3
Длина радиус-вектора точки М называется модулем комплексного числа z и обозначается | z | или r:
(6)
Угол j, образованный этим вектором с положительным направлением действительной оси Ох, называется аргументом числа z. Связь между аргументом j комплексного числа и его действительной и мнимой частью выражается формулами:
(7)
или
(8)
Аргумент комплексного числа определен неоднозначно: если j – аргумент числа z, то 
– также аргумент этого числа при любом целом k. Для однозначности определения аргумента его выбирают в пределах 
такое значение аргумента называют главным и обозначают 
Всюду далее будем рассматривать главное значение аргумента: 
На практике находить аргумент комплексного числа z имеет смысл согласно формуле (7.32) с учетом координатной четверти, в которой лежит число z, или формул (7.33).
Запись комплексного числа в виде
(9)
называется тригонометрической формой комплексного числа.
Пусть 
и 
комплексные числа, заданные в тригонометрической форме. Тогда для произведения 
и частного 
справедливы формулы:
(10)
(11)
Для комплексного числа 
справедлива формула Муавра:
(12)
Корнем n-й степени из комплексного числа z называется комплексное число w такое, что 
Корень n -й степени из комплексного числа
имеет n различных значений, которые находят по формуле
(13)
где 
– арифметическое значение корня.
Все значения корня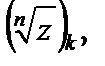 
расположены на окружности с центром в начале системы координат и радиусом 
в вершинах правильного вписанного в окружность n -угольника.
Соотношение
|
|
(14)
называется формулой Эйлера.
Пусть комплексное число z записано в тригонометрической форме. Используя формулу Эйлера (7.39), можно записать:
(7.40)
Такая форма записи называется показательной формой комплексного числа.