Поле постоянного электрического тока и его свойства

Теория решения задач электроразведки базируется на системе уравнений электродинамики – уравнениях Дж. К. Максвелла. Эти уравнения, описывающие законы распространения электромагнитных полей в неоднородной проводящей среде, записываются в виде:

(1.2)

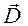где и - векторы электрического и магнитного полей, и - векторы электрической и магнитной индукции, - плотность электрических зарядов, - вектор плотности токов проводимости. Следствием первого и четвертого уравнений системы является уравнение непрерывности:

(1.3)

Уравнения Максвелла дополняются уравнениями связи между векторами , , 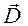и :

, (1.4)

а также законом Ома в дифференциальной форме:

, (1.5)

где , и - электромагнитные свойства среды: электропроводность, диэлектрическая и магнитная проницаемости соответственно.

Первое уравнение Максвелла представляет собой дифференциальное выражение закона полного тока, согласно которому циркуляция магнитного поля по замкнутому контуру равна полному току в нем. Оно указывает, что магнитное поле порождается как токами проводимости (первое слагаемое в правой части уравнения), так и токами смещения (второе слагаемое). Причем токи проводимости - это движение зарядов, а токи смещения - скорость изменения электрической индукции.

Второе уравнение есть дифференциальное выражение закона электромагнитной индукции, согласно которому изменение магнитной индукции возбуждает вихревое электрическое поле. Таким образом, переменное магнитное поле порождает переменное электрическое, постоянное же магнитное поле электрического не создает.

Третье уравнение указывает, что в природе магнитных зарядов не существует, и силовые линии поля магнитной индукции замкнуты.

Четвертое уравнение говорит, что источниками поля электрической индукции являются электрические заряды. Изолинии поля электрической индукции начинаются на этих зарядах и непрерывны вне их.

Известно, что глубина проникновения возбуждаемого электрического тока прямо пропорциональна длине волны или обратно пропорциональна частоте тока . Поэтому можно регулировать глубину проникновения тока в землю, изменяя его частоту. Чтобы достигнуть глубоких горизонтов исследований в электроразведке используются поля низких частот. Учитывая то, что законы распространения токов низкой частоты в земле с высокой степенью точности совпадают с законами распространения полей постоянного тока, то становится очевидной важность изучения математических моделей распространения электрических полей постоянного тока в геофизике.

Основной моделью в этом случае становится стационарная модель электромагнитного поля, когда рассматривается поле, не зависящее от времени. Стационарная модель получается из системы уравнений максвелла следующим образом.

В области, где среда однородна, электрические заряды не существуют (точнее, быстро после своего появления рассасываются). Учитывая также уравнения связи, уравнения Максвелла в однородной среде записывается в виде:

(1.6)

Теперь можно разделить уравнения Максвелла, то есть выделить электрическую и магнитную составляющие электромагнитного поля. Для этого применим операцию rot к обеим частям первого уравнения Максвелла:

. (1.7)

Из теории поля известно, что для произвольного вектора

. (1.8)

Используя соотношение (1.8), можно записать:

Учитывая второе и третье уравнения системы (1.6), получим телеграфное уравнение для вектора :

. (1.9)

Если за исходное принять второе уравнение Максвелла, то после аналогичных преобразований получим телеграфное уравнение для вектора :

(1.10)

Если поле постоянно, и при этом в среде текут токи проводимости, то телеграфные уравнения преобразуются в уравнения Лапласа

, (1.11)

а в уравнениях Максвелла исчезают производные по времени.

В такой стационарной модели, путем зануления всех производных по времени, выделим из системы уравнения для электрической составляющей поля:

. (1.12)

Для существования постоянного пространственного тока в земле необходимо, чтобы в ней непрерывно действовали сторонние силы [10], или, что одно и тоже, действовали источники или стоки тока, интенсивность которых описывается функцией в уравнении .

Из системы (1.12) следует, что электрическое поле является безвихревым или потенциальным, т.е. , где функция - потенциал электрического поля.

В итоге имеем систему уравнений стационарного электрического поля постоянного тока:

, , . (1.13)

Первое уравнение (1.13) – есть соотношение между потенциалом и напряженностью поля, второе является законом Ома, а третье – законом Кирхгофа в дифференциальной форме.

Если пространство изотропно, то удельная электрическая проводимость среды - величина скалярная в каждой точке. В дальнейшем будем рассматривать поле в изотропном пространстве.

Подставляя первое уравнение (1.13) во второе, а затем второе в третье, получим основное дифференциальное уравнение электроразведки

. (1.14)

Уравнение (1.14) в полной записи имеет вид:

(1.15)

Неоднородную по электрической проводимости среду с определенной степенью достоверности можно представить в виде объединения однородных и изотропных сред постоянной проводимости с кусочно-гладкими границами раздела Липшицевого типа.

Если рассматривать среды, в которых удельная электрическая проводимость - есть кусочно-постоянная функция, то в области постоянной проводимости при наличии в ней источников тока уравнение (1.14) преобразуется в уравнение Пуассона:

. (1.16)

Если к тому же в области отсутствуют источники или стоки тока, т.е. , то уравнение (1.14) превращается в уравнение Лапласа:

. (1.17)

Функция правой части уравнения (1.15) описывает интенсивность источников постоянного тока. В качестве источника на практике применяют линейные, кольцевые, точечные источники, а также электроды с распределенными по некоторым замкнутым или незамкнутым поверхностям источниками.

Если поверхность электрода представить совокупностью точечных источников - элементарных поверхностей малых размеров, то поле объемного электрода и поле точечного источника, при размещении их на расстояние 5-10 характерных размеров друг от друга, мало различимы [137]. Тогда, т.к. задача (1.15)-линейная и для нее соблюдается принцип суперпозиции электрических полей, достаточно рассмотреть случай, когда в качестве источника используется точечный электрод с интенсивностью I.

В качестве функции будем рассматривать функцию вида , где - точка, содержащая источник тока силы , 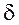- есть функция Дирака, обладающая следующими свойствами [63]:

Обозначая координаты точки через , а координаты точки - через , будем иметь

.

Решение уравнения (1.14), как правило, отыскивается в неограниченном пространстве или в полупространстве с кусочно-непрерывной функцией . Для однозначного определения функции задаются краевые условия на границе многосвязной области , на линиях и поверхностях разрыва функции .

Условия на границе - изолятора и среды, за счет растекания тока по ее поверхности, имеют вид:

, (1.18)

где - направление внешней нормали к , в частности, на границе раздела сред «земля-воздух» - дневной поверхности, вводится условие: .

Аналогичное (1.18) условие ставится и на плоскостях пространственной симметрии электрического тока. Это позволяет рассматривать задачу для одного из полупространств с уменьшенной в половину силой тока .

На границе контакта двух сред и удельной электрической проводимости и соответственно могут быть условия ():

- первого рода, ; (1.19)

- второго рода, ; (1.20)

- третьего рода ; (1.21)

- четвёртого рода ; (1.22)

- пятого рода . (1.23)

Условие (1.22) является условием непрерывности потенциала и плотности тока на границе разрыва функции .

Равенство нулю потенциала тока на бесконечности (1.23) (условие регулярности решения) согласуется с понятием потенциала как работы по перемещению заряда из бесконечно удаленной точки в точку в силовом поле, образуемом источником тока в точке .

Единственность задачи (1.14)-(1.23) обоснована в работе А.Н. Тихонова [346].

Замечание. Основные допущения модели:

1. Среда изотропна, кусочно-однородная, т.е. в некоторой области, св-ва этой среды одинаковы.
2. Источник тока – точечный.
3. Электрический ток – постоянный, т.е. частота = 0.