▼ Одним из важнейших результатов в теории вероятностей является центральная предельная теорема, которая устанавливает предельное распределение для нормированных и центрированных сумм независимых случайных величин. Здесь приведена формулировка, принадлежащая П. Леви.
Теорема 4.1 ( Теорема Леви ). Пусть  независимые случайные величины, имеющие одинаковые распределения. Обозначим
независимые случайные величины, имеющие одинаковые распределения. Обозначим  Тогда
Тогда  при
при 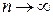 .
.
Здесь 
 функция распределения стандартного нормального закона.
функция распределения стандартного нормального закона.
Отметим, что интегральная предельная теорема Муавра  Лапласа, рассмотренная при исследовании схемы Бернулли, является частным случаем теоремы Леви. Она получается, если в теореме Леви положить
Лапласа, рассмотренная при исследовании схемы Бернулли, является частным случаем теоремы Леви. Она получается, если в теореме Леви положить  , если в i -м испытании был успех,
, если в i -м испытании был успех,  в противном случае, i =1, 2,..., n. ▲
в противном случае, i =1, 2,..., n. ▲
Задача 4.1. Игральный кубик бросили 100 раз. Приближенно найти вероятность того, что сумма выпавших очков попадает в интервал (340, 360).
Решение. Пусть  число выпавших очков при i -м бросании, i ≤ n, S
число выпавших очков при i -м бросании, i ≤ n, S  сумма выпавших очков. Тогда так определенные случайные величины
сумма выпавших очков. Тогда так определенные случайные величины  независимы и имеют одинаковые распределения.
независимы и имеют одинаковые распределения. 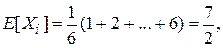


В соответствии с табл. 4.1,


Таблица 4. 1.
Функция распределения стандартного нормального распределения
| x | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| 0.0 | 0.5000 | 0.5040 | 0.5080 | 0.5120 | 0.5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
| 0.1 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 | 0.5636 | 0.5675 | 0.5714 | 0.5753 |
| 0.2 | 0.5793 | 0.5832 | 0.5871 | 0.5910 | 0.5948 | 0.5987 | 0.6026 | 0.6064 | 0.6103 | 0.6141 |
| 0.3 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6331 | 0.6368 | 0.6406 | 0.6443 | 0.6480 | 0.6517 |
| 0.4 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.6700 | 0.6736 | 0.6772 | 0.6808 | 0.6844 | 0.6879 |
| 0.5 | 0.6915 | 0.6950 | 0.6985 | 0.7019 | 0.7054 | 0.7088 | 0.7123 | 0.7157 | 0.7190 | 0.7224 |
| 0.6 | 0.7257 | 0.7291 | 0.7324 | 0.7357 | 0.7389 | 0.7422 | 0.7454 | 0.7486 | 0.7517 | 0.7549 |
| 0.7 | 0.7580 | 0.7611 | 0.7642 | 0.7673 | 0.7704 | 0.7734 | 0.7764 | 0.7794 | 0.7823 | 0.7852 |
| 0.8 | 0.7881 | 0.7910 | 0.7939 | 0.7967 | 0.7995 | 0.8023 | 0.8051 | 0.8078 | 0.8106 | 0.8133 |
| 0.9 | 0.8159 | 0.8186 | 0.8212 | 0.8238 | 0.8264 | 0.8289 | 0.8315 | 0.8340 | 0.8365 | 0.8389 |
| 1.0 | 0.8413 | 0.8438 | 0.8461 | 0.8485 | 0.8508 | 0.8531 | 0.8554 | 0.8577 | 0.8599 | 0.8621 |
| 1.1 | 0.8643 | 0.8665 | 0.8686 | 0.8708 | 0.8729 | 0.8749 | 0.8770 | 0.8790 | 0.8810 | 0.8830 |
| 1.2 | 0.8849 | 0.8869 | 0.8888 | 0.8907 | 0.8925 | 0.8944 | 0.8962 | 0.8980 | 0.8997 | 0.9015 |
| 1.3 | 0.9032 | 0.9049 | 0.9066 | 0.9082 | 0.9099 | 0.9115 | 0.9131 | 0.9147 | 0.9162 | 0.9177 |
| 1.4 | 0.9192 | 0.9207 | 0.9222 | 0.9236 | 0.9251 | 0.9265 | 0.9279 | 0.9292 | 0.9306 | 0.9319 |
| 1.5 | 0.9332 | 0.9345 | 0.9357 | 0.9370 | 0.9382 | 0.9394 | 0.9406 | 0.9418 | 0.9429 | 0.9441 |
| 1.6 | 0.9452 | 0.9463 | 0.9474 | 0.9484 | 0.9495 | 0.9505 | 0.9515 | 0.9525 | 0.9535 | 0.9545 |
| 1.7 | 0.9554 | 0.9564 | 0.9573 | 0.9582 | 0.9591 | 0.9599 | 0.9608 | 0.9616 | 0.9625 | 0.9633 |
| 1.8 | 0.9641 | 0.9649 | 0.9656 | 0.9664 | 0.9671 | 0.9678 | 0.9686 | 0.9693 | 0.9699 | 0.9706 |
| 1.9 | 0.9713 | 0.9719 | 0.9726 | 0.9732 | 0.9738 | 0.9744 | 0.9750 | 0.9756 | 0.9761 | 0.9767 |
| 2.0 | 0.9772 | 0.9778 | 0.9783 | 0.9788 | 0.9793 | 0.9798 | 0.9803 | 0.9808 | 0.9812 | 0.9817 |
| 2.1 | 0.9821 | 0.9826 | 0.9830 | 0.9834 | 0.9838 | 0.9842 | 0.9846 | 0.9850 | 0.9854 | 0.9857 |
| 2.2 | 0.9861 | 0.9864 | 0.9868 | 0.9871 | 0.9875 | 0.9878 | 0.9881 | 0.9884 | 0.9887 | 0.9890 |
| 2.3 | 0.9893 | 0.9896 | 0.9898 | 0.9901 | 0.9904 | 0.9906 | 0.9909 | 0.9911 | 0.9913 | 0.9916 |
| 2.4 | 0.9918 | 0.9920 | 0.9922 | 0.9925 | 0.9927 | 0.9929 | 0.9931 | 0.9932 | 0.9934 | 0.9936 |
| 2.5 | 0.9938 | 0.9940 | 0.9941 | 0.9943 | 0.9945 | 0.9946 | 0.9948 | 0.9949 | 0.9951 | 0.9952 |
| 2.6 | 0.9953 | 0.9955 | 0.9956 | 0.9957 | 0.9959 | 0.9960 | 0.9961 | 0.9962 | 0.9963 | 0.9964 |
| 2.7 | 0.9965 | 0.9966 | 0.9967 | 0.9968 | 0.9969 | 0.9970 | 0.9971 | 0.9972 | 0.9973 | 0.9974 |
| 2.8 | 0.9974 | 0.9975 | 0.9976 | 0.9977 | 0.9977 | 0.9978 | 0.9979 | 0.9979 | 0.9980 | 0.9981 |
| 2.9 | 0.9981 | 0.9982 | 0.9982 | 0.9983 | 0.9984 | 0.9984 | 0.9985 | 0.9985 | 0.9986 | 0.9986 |
| 3.0 | 0.9987 | 0.9987 | 0.9987 | 0.9988 | 0.9988 | 0.9989 | 0.9989 | 0.9989 | 0.9990 | 0.9990 |
| 3.1 | 0.9990 | 0.9991 | 0.9991 | 0.9991 | 0.9992 | 0.9992 | 0.9992 | 0.9992 | 0.9993 | 0.9993 |
| 3.2 | 0.9993 | 0.9993 | 0.9994 | 0.9994 | 0.9994 | 0.9994 | 0.9994 | 0.9995 | 0.9995 | 0.9995 |
| 3.3 | 0.9995 | 0.9995 | 0.9995 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9997 |
| 3.4 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9998 |
Задача 4.2. Количество вызовов в течение суток на станцию скорой помощи имеет распределение Пуассона с  = 73. Количества вызовов в разные сутки не зависят друг от друга. Определить вероятность того, что в течение года (365 дней) общее число вызовов будет в пределах от 26 500 до 26 800.
= 73. Количества вызовов в разные сутки не зависят друг от друга. Определить вероятность того, что в течение года (365 дней) общее число вызовов будет в пределах от 26 500 до 26 800.
Решение. Пусть  число вызововв i -й день года, i ≤ 365, S
число вызововв i -й день года, i ≤ 365, S  число вызовов в течение года, n = 365.
число вызовов в течение года, n = 365.
Тогда 
Из центральной предельной теоремы получим


Задача 4.3. Опыт состоит в том, что два игрока одновременно бросают по игральному кубику, выигрыш (проигрыш) каждого из них (в рублях) равняется разности очков на их кубиках. Произведено 100 таких опытов. Найти вероятность того, что суммарный выигрыш первого игрока больше 10 р.
Решение. Пусть  выигрыш первого игрока в i -м опыте. Тогда
выигрыш первого игрока в i -м опыте. Тогда  где
где  число очков на кубиках первого и второго игроков соответственно. Вычислим математические ожидания и дисперсии случайных величин
число очков на кубиках первого и второго игроков соответственно. Вычислим математические ожидания и дисперсии случайных величин  :
:




Обозначив через 
 суммарный выигрыш первого игрока, применим центральную предельную теорему:
суммарный выигрыш первого игрока, применим центральную предельную теорему:
 .
.
Список литературы
1. Методы решения задач по теории вероятностей (дискретные распределения): Методические указания к решению задач. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2007.
2 Бородин А. Н.Элементарный курс теории вероятностей и математической статистики. СПб.: Лань, 1998.
3 Вентцель Е. С., Овчаров Л. А. Теория вероятностей. М.: Наука, 1969.
4. Викулов Э. А., Ефимов А. В., Земсков В. Н. и др. Сборник задач по математике для ВТУЗОВ М.: Наука, 1990.
ПРИЛОЖЕНИЕ