Площадь заштрихованной части подграфика плотности стандартного нормального закона задается формулой  и представляет собой функцию распределения,
| 
|
соответствующую этой плотности распределения. Значения функции распределения, равные отмеченной на рисунке площади, приведены в табл. 4.1.
Пусть, например, требуется найти 
. Ближайшие табличные значения: 
и 
(используем строку 1.4 и столбцы, соответственно, 0.07 и 0.08). В качестве грубой оценки (округляя 
до 1.47) можно взять 
, для получения более точного результата следует применить линейную интерполяцию:
Смысл этой операции: к стартовому значению 0.9292 прибавляется приращение функции на рассматриваемом промежутке (0.0014), умноженное на относительное смещение аргумента 
(0.36). Аналогично решается обратная задача — восстановление 
по известному значению 
. Пусть, например, 
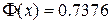. Ближайшие табличные значения: 
и 
. Грубое приближение: 
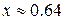(для него табличное значение наиболее близко к требуемому). Уточняем с помощью обратной интерполяции:
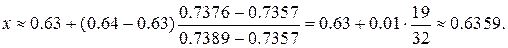
В таблицах обычно приводят значения только для положительных аргументов, поскольку функция нормального распределения обладает определенной симметрией: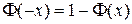 
. Например, 
= 
. При больших значениях функция 
(как и вообще любая функция распределения) стремится к единице, причем быстро. Если все же требуется найти отклонение от 1, то можно воспользоваться грубой оценкой 
; при 
относительная погрешность этой формулы меньше 10 % и далее убывает примерно как 
. В литературе часто используются немного другие функции, связанные с нормальным распределением. Приведем две из них.
1. Функция Лапласа 
. Она определена из соображений нечетности 
и нормировки 
. Связь с функцией нормального распределения имеет следующий вид:
; 
.
2. Интеграл ошибок 
. Эта функция удовлетворяет тем же условиям нечетности и нормировки: 
, 
. Связь с функцией нормального распределения:
; 
.
Термин «интеграл ошибок» объясняется тем, что случайные погрешности измерений обычно считаются распределенными по нормальному закону. Причина — в центральной предельной теореме: на эти погрешности влияет большое количество неконтролируемых факторов, которые условно можно считать независимыми. Следует подчеркнуть, что в литературе можно встретить разные обозначения для рассматриваемых функций (более или менее устойчиво определяется лишь интеграл ошибок). Например, в некоторых справочниках через обозначена деленная на 2 функция Лапласа, в то время как функция нормального распределения обозначается как 
. Обращать внимание надо не на обозначения, а на то, какими конкретно интегралами эти функции определяются.В системе MathCAD определены интеграл ошибок erf (x) и функция нормального распределения cnorm (x), а также обратная к ней функция qnorm (p, m, s) (m — математическое ожидание и s — среднеквадратическое отклонение; p = cnorm (x) соответствует x = qnorm (p, 0, 1). В системе Matlab erf (x) — это также интеграл ошибок; обратная к нему функция обозначается erfinv (x).
Содержание
ВВЕДЕНИЕ. 3
1. ОДНОМЕРНЫЕ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН.. 3
2. СОВМЕСТНОЕ РАСПРЕДЕЛЕНИЕ НЕСКОЛЬКИХ СЛУЧАЙНЫХ ВЕЛИЧИН 14
3. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН.. 18
4. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА.. 25
Функция нормального распределения. 29
Редактор И. Г. Скачек
_________________________________________________________________
Подписано в печать Формат 60×84 1/16.
Бумага офсетная. Печать офсетная. Печ. л.2.0.
Гарнитура «Times Roman». Тираж 250 экз. Заказ
_________________________________________________________________
Издательство СПбГЭТУ «ЛЭТИ»
197376, С.-Петербург, ул. Проф. Попова, 5