Множественная корреляция

Множественная регрессия и корреляция

3.1. Методические указания

 

Модели множественной регрессии

Множественная регрессия – уравнение связи с несколькими независимыми переменными:

где у – зависимая переменная (результативный признак);

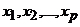– независимые переменные (факторы).

Для построения уравнения множественной регрессии чаще всего используются следующие функции:

– линейная ;

– степенная ;

– экспонента ;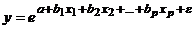

– гипербола .

Можно использовать и другие функции, приводимые к линейно­му виду.

Оценка параметров множественной линейной регрессии

Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение кото­рой позволяет получить оценки параметров регрессии:

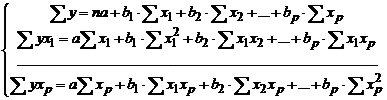
Для ее решения может быть применён метод определителей (правило Крамера):

где – определитель системы;

– частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.

Стандартизованное уравнение регрессии

Другой вид уравнения множественной регрессии – уравнение регрессии в стандартизованном масштабе:

,

где 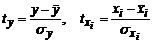– стандартизованные переменные;

– стандартизованные коэффициенты регрессии.

К уравнению множественной регрессии в стандартизованном масштабе применим МНК. Стандартизованные коэффициенты регрессии (b -коэффициенты) определяются из следующей системы уравнений:

Связь коэффициентов множественной регрессии со стандарти­зованными коэффициентами описывается соотношением

.

Параметр а определяется как .

Частные уравнения регрессии

На основе линейного уравнения множественной регрессии

могут быть найдены частные уравнения регрессии:

т. е. уравнения регрессии, которые связывают результативный признак с соответствующими факторами х при закреплении дру­гих учитываемых во множественной регрессии факторов на сред­нем уровне. Частные уравнения регрессии имеют следующий вид:

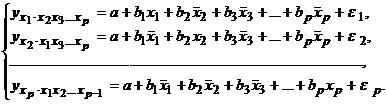
При подстановке в эти уравнения средних значений соответ­ствующих факторов они принимают вид парных уравнений ли­нейной регрессии, т. е. имеем:

где

В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному чле­ну уравнения множественной регрессии. Это позволяет на осно­ве частных уравнений регрессии определять частные коэффици­енты эластичности:

(3.4)

где - коэффициенты регрессии для фактора х_i в уравнении множественной регрессии;

- частное уравнение регрессии.

Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле:

.

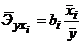Множественная корреляция

Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции:

.

Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:

.

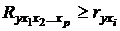Индекс множественной корреляции для уравнения в стандартизованном масштабе можно записать в виде

.

При линейной зависимости коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции:

,

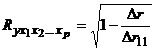где – определитель матрицы парных коэффициентов корреляции;

 

– определитель матрицы межфакторной корреляции.

 

Качество построенной модели в целом оценивает коэффициент (индекс) детерминации. Коэффициент множественной детермина­ции рассчитывается как квадрат индекса множественной корреля­ции .

Скорректированный индекс множественной детерминации со­держит поправку на число степеней свободы и рассчитывается по формуле

,

где п – число наблюдений; т – число факторов.

Частная корреляция

Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора 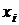при неизменном уровне других факторов, можно определить по формуле

или по рекуррентной формуле

.

Частные коэффициенты корреляции изменяются в пределах от -1до1.

Прямыми вычислениями можно показать, что для двухфакторной модели справедлива следующая формула, связывающая коэффициенты частной и обычной корреляции:

Существует тесная связь между коэффициентом частной корреляции и коэффициентом детерминации , а именно

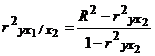или .