Теория вероятностей.
1. Понятие о вероятности события, различные оценки вероятности случайной величины: классическое определение вероятности случайного события, геометрическая вероятность, статистическая вероятность и примеры их.
Основным понятием теории вероятностей является понятие случайного события. Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти. Например, попадание в некоторый объект или промах при стрельбе по этому объекту из данного орудия является случайным событием.
Событие называется достоверным, если в результате испытания оно обязательно происходит. Невозможным называется событие, которое в результате испытания произойти не может.
Случайные события называются несовместными в данном испытании, если никакие два из них не могут появиться вместе.
Случайные события образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними.
Рассмотрим полную группу равновозможных несовместных случайных событий. Такие события будем называть исходами. Исход называется благоприятствующим появлению события А, если появление этого события влечет за собой появление события А.
Вероятностью события A называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместных элементарных исходов, образующих полную группу
Свойство 1. Вероятность достоверного события равна единице
Свойство 2. Вероятность невозможного события равна нулю.
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Итак, вероятность любого события удовлетворяет двойному неравенству 
.
Геометрическая вероятность события А определяется отношением:
,
где m(G), m(A) – геометрические меры (длины, площади или объемы) всего пространства элементарных исходов и события А.
Статистическое определение вероятности 
. Часто оказывается довольно сложно представить результат испытания в виде совокупности элементарных событий. Кроме того, не всегда элементарные события равновероятны. Например, когда студент идет на экзамен, четыре элементарных события — оценка 2, 3, 4, 5 — равновероятными не являются. В подобных случаях наряду с классическим используют статистическое определение вероятности. В качестве статистической вероятности события принимается относительная частота его реализации при большом числе испытаний. Если проводится n испытаний и при этом событие А реализовалось m раз, то относительная частота появления события А есть 
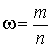.Например, если монета подбрасывалась 2000 раз, и орел при этом выпал 982 раза, то статистическая вероятность события, что выпадет орел, равна относительной частоте его появления 
.
2. Теорема сложения вероятностей несовместных событий. Теорема умножения вероятностей независимых событий.
Теорема сложения. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р (А + В) = Р (А) + Р (В).
Доказательство
С л е д с т в и е. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р (A1 + A2 +... + An) = Р (A1) + Р (A2) +... + Р (An).
Для независимых событий теорема умножения Р (АВ) = Р (А) РA (В) имеет вид
Р (АВ) = Р (А) Р (В), (**)
т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
3. Теорема сложения вероятностей совместных событий. Зависимые и независимые события. Условная вероятность. Формула полной вероятности.
Теорема сложения вероятностей формулируется следующим образом.
Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:
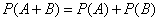
Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависимыми.
Условной вероятностью 
(два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
Если событие А может произойти только при выполнении одного из событий 
, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
.
Эта формула называется формулой полной вероятности.
4. Дискретная, случайная величина. Закон распределения, многоугольник распределения. Функция распределения вероятностей. Математическое ожидание, дисперсия дискретной, случайной величины, их свойства. Среднеквадратическое отклонение.
Случайной называют величину, которая в результате испытания примет случайно одно и только одно значение из множества возможных значений.
Дискретной (прерывной) называют случайную величину, которая принимает отдельные возможные значения с определенными вероятностями.
Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями (его можно задать таблично, аналитически (в виде формулы) и графически.
Закон распределения дискретной случайной величины можно изобразить графически, введя прямоугольную систему координат ХОР, отметив в ней точки (хi, pi) и соединив их. Полученная фигура называется многоугольником распределения.
ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ —
вероятность того, что случайная величина X примет значение, меньшее, чем х, где х — произвольное действительное число: F(x) = Р{Х ≤ х} =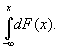 
F(x) — неубывающая функция; О ≤ F(x) ≤ 1. Ф. р. в. полностью задает случайную величину. Если X — дискретная случайная величина, принимающая значения х1, x2... с вероятностями p1,p2,..., то ее функция распределения будет: F(x) = ∑ рk; она разрывна и возрастает скачками в точках хk. Если X — непрерывная случайная величина, то у нее существует платность распределения вероятностей f(x) и Ф. р. в. будет:
.
Математи́ческое ожида́ние — среднее значение случайной величины. Математическое ожидание Mx случайной величины x равно
|
Дисперсией называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
D (X) = M (X 2) - (M (X)) 2. - для дискретной случайной величины;
Дисперсией случайной величины x называется среднее значение квадрата отклонения случайной величины от её математического ожидания:
|
Используя вероятности pi того, что величина x принимает значения xi, эту формулу можно переписать следующим образом:
Среднеквадратическим отклонением случайной величины x называется корень квадратный из дисперсии этой величины:
|
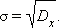
5. Схема и формула Бернулли (сочетания и вычисление их количества). Биномиальное распределение. Математическое ожидание и дисперсия биномиального распределен™.
Формула Бернулли — формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний.
Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:
где Cnk — число сочетаний, q = 1 − p.
Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A, причем известна вероятность этого события P (A) = p. Требуется определить вероятность того, что при проведении n испытаний событие A появится ровно k раз.
— появление события A с вероятностью p;
«не А» — событие А не появилось, что происходит с вероятностью q = 1 − p.
Важнейшее условие, без которого схема Бернулли теряет смысл — это постоянство. Сколько бы опытов мы ни проводили, нас интересует одно и то же событие A, которое возникает с одной и той же вероятностью p.
Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из 
независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна и равна 
.
Мат. ожидание и дисперсия биноминального распределения
Биноминальное распределение - p(X=m)= Cnm pmqn"m Математическое ожидание ЕХ=пр Дисперсия DX=npq
6. Графики функции распределения и плотности распределения вероятностей непрерывной, случайной величины на примерах равномерного и нормального распределения. Свойства графиков. Числовые характеристики указанных случайных величин.
Вероятностное пространство - (Q, F, Р)
Q - множество элементов (ели оно конечно, то пространство дискретное) F - событие Р - вероятность
Случайной величиной называется функция, заданная на Q. X=X(w), wG Q
{ш: Х(ы)<а} GF для всех a GR[1]{w:X(w) GB} G F для всех В eft
ft - о-алгебра борелевских множеств - содержит все конечное объединение интервалов (и бесконечные множества) Р(Х(ш)) GB)
Опр. Рассмотрим р(В)=Р(саз:Х(оо) GB)
|j(B) - задана на множестве В G ft
|j(B) - распределение случайной величины X.
Функция распределения случайной величины.
F(x)=P(X<x)=P (w:X(w)<x)
P(a<=X<b)= м([а,Ь))= мИ, b) - M(-~,a)=F(b)-F(a)
A= Uie(i..n)[ai,bi)
P(X GA)= M(Uie(i..n)[abb,))=Z,e(i..n) M([aj,bi»= Iie(i..n)(P(X<bi) - Р(Х<аО)
Свойства функции распределения.
1. 0<=F(x) <=1
2. F(x) не убывает
3. 1) Mm F(x)=1 при х-> °° 2) Mm F(x)=0 при х->
4. F(x) - непрерывна слева, приближается к х слева
Это полный набор свойств. Если хотя бы одно свойство не выполнено, то это не функция распределения.
Свойства плотностей распределения.
Случайная величина X имеет дискретное распределение, если ее множество значений конечно. p(X=xk)=p(xk), xk пробегает всевозможные значения X. р(хк) - дискретная плотность распределения. F(X)=p(X<x)=Ixk<x p(xk)
Свойства дискретной плотности распределения.
1. р(х)>=0, р(х)<=1
2. Ikp(Xk)=1
Случайная величина X имеет абсолютное непрерывное распределение, если существует такая функция р(х)>=0, т.ч. F(x)= f.oo p(t) dt
р(х) - плотность распределения случайной величины X. p(x)=F'(x) Свойства плотности распределения.
1. р(х)>=0
2. Г"- р(х) dx =1
7. Вероятность попадания значений в заданный интервал. Правило 3 сигм для нормального распределения. Таблица Лапласа.
Нормальное распределение (синоним - гауссово распределение) - распределение непрерывной случайной величины с плотностью
Здесь "мю" - математическое ожидание, "сигма" - среднеквадратическое отклонение (корень квадратный из дисперсии). Такой вариант задания плотности распределения позволяет легко отыскивать математическое ожидание и дисперсию в случае нормального распределения. Строго говоря, сейчас было задано множество различных распределений, элементы которого отличаются значениями двух параметров. При конкретных значениях этих параметров получаем вполне конкретное распределение.
График плотности распределения для нормально распределённой случайной величины имеет вид, отдалённо напоминающий колокол:
Точка наивысшего подъёма данного графика - математическое ожидание случайной величины. Как нетрудно догадаться, при реальных испытаниях в большом количестве или крупных экспериментальных выборках очень высокий процент полученных случайных значений будет приходиться на узкий диапазон, включающий в себя математическое ожидание и некую "округу". Значения, находящиеся далеко от "высшей" точки, встречаются редко, являясь "аномалией". Дальше мы об этом ещё поговорим.
Функция распределения не может быть записана через элементарные функции, поскольку интеграл от плотности распределения "неберущийся". Поэтому её записывают вот так:
Вероятность того, что непрерывная случайная величина окажется каким-либо действительным числом, равна единице, поскольку полагается, что величина может принимать значение только на множестве действительных чисел. Поэтому
Стандартное нормальное распределение
Нормальное распределение с нулевым математическим ожиданием и единичной дисперсией называется стандартным нормальным распределением. Вот так в данном случае выглядят плотность и функция распределения.
Правило трёх сигм
Выше значения, далёкие от математического ожидания, были обозваны "аномальными". Обратите внимание, как распределение сильно "концентрируется" около одной точки.
Вероятность того, что случайное значение окажется отдалено от точки максимума более, чем на три "сигмы", очень близка к нулю, составляя примерно 0,003. Этот факт известен как правило трёх сигм.