, (12.1)
а затем ключом К замкнуть контур, конденсатор начнет разряжаться через катушку и в цепи появится быстро нарастающий ток. Согласно закону Фарадея, этот ток вызовет на концах катушки ЭДС самоиндукции, имеющую знак, противоположный знаку разности потенциалов на обкладках конденсатора. Вследствие этого скорость нарастания тока в контуре будет постепенно уменьшаться до тех пор, пока конденсатор полностью не разрядится. В этот момент сила тока в цепи будет максимальна. Энергия электрического поля конденсатора перейдёт в энергию магнитного поля катушки
. (12.2)
В дальнейшем ток, сохраняя свое прежнее направление, перезаряжает конденсатор. На его обкладках появляется разность потенциалов, противоположная по знаку первоначальной, что приводит к уменьшению тока, а значит, и магнитного поля катушки. Возникающая при этом ЭДС самоиндукции будет поддерживать уменьшающийся ток. В момент времени, когда ток прекратится, конденсатор полностью перезарядится: заряд, разность потенциалов на его обкладках и ЭДС самоиндукции будут максимальны. После этого вновь начинается разряд конденсатора через катушку и процесс повторяется в противоположном направлении.
Найдём зависимость заряда на обкладках конденсатора от времени. Из закона сохранения энергии следует, что убыль энергии электрического и магнитного полей в реальном контуре равна количеству выделенного контуром тепла:
. (12.3)
Считая, что индуктивность L не зависит от времени, проведём дифференцирование и обозначим:
. (12.4)
Получим
. (12.5)
Решение этого дифференциального уравнения при δ<< w0 имеет вид
, (12.6)
где 
– циклическая частота колебаний, 
– круговая частота свободных незатухающих колебаний, Q 0– начальный заряд конденсатора, j0– начальная фаза, 
– коэффициент затухания – величина, обратная промежутку времени t, в течение которого амплитуда убывает в e раз. Величину t называют временем релаксации.
Выражение (12.6) можно представить в виде, похожем на гармонические колебания:
, (12.7)
где 
– амплитуда колебаний заряда, которая, в отличие от гармонических колебаний, не является постоянной, а уменьшается со временем по экспоненте.
График функции (12.6) представлен на рис. 12.2. Подобным же образом будут изменяться сила тока в контуре и разность потенциалов на обкладках конденсатора.
Из рис. 12.2 видно, что хотя затухающие колебания не являются периодическими в строгом смысле этого слова, этот процесс обладает определенной повторяемостью: максимальные и минимальные значения заряда, тока и разности потенциалов достигаются через одинаковые промежутки времени Т.
Эту величину и называют периодом свободных затухающих колебаний(условным периодом)
. (12.8)
Наряду с коэффициентом затухания δ пользуются и другой величиной– логарифмическим декрементом затухания θ. Он равен натуральному логарифму отношения двух последовательных амплитуд, разделённых промежутком времени, равным периоду колебаний Т:
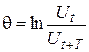. (12.9)
Можно показать, что
. (12.10)
Из выражения (12.8) видно, что с увеличением сопротивления контура период колебаний в нём возрастает и при условии
(12.11)
обращается в бесконечность. Это значит, что колебания в контуре не возникают. Наступает апериодический разряд, характер которого показан на рис. 12.3. Минимальное сопротивление контура, при котором не возникают колебания, называется критическим. Его можно определить по формуле:
. (12.12)