Определение. Биномиальное распределение — распределение количества наступлений события A в последовательности из n независимых случайных экспериментов, таких, что вероятность наступления события A в каждом из них постоянна и равна p.
Формула Бернулли является аналитическим выражением искомого закона распределения.
Таблица №1
| Математическое ожидание | np |
| Дисперсия | npq |
Задача №1.
Стрелок стреляет 9 раз по мишени. Вероятность попадания в цель при одном выстреле Написать в виде теблицы (матрицы) закон распределения случайной величины X – число попаданий по мишени. Проверить, что сумма всех вероятностей в таблице равна 1. Найти по формулам (1) и (2) математическое ожидание и дисперсию. Подтвердить полученные результаты по формулам из таблицы №1. Найти среднее квадратическое отклонение. Найти вероятность того, что стрелок попадет более 5 раз по мишени.
Решение.
Формула Бернулли:
> 

Матрица распределения:
> 

Проверим, что сумма всех вероятностей во второй строке равна 1.
> 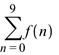

Найдем математическое ожидание:
> 

> 

По формуле: результат подтверждается.
Найдем дисперсию:
> 

> 

По формуле: результат подтверждается.
Найдем среднее квадратическое отклонение:
> 

> 

Вероятность того, что стрелок попадет более 5 раз равна:
> 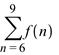

> 

76, 16%.
Распределение Пуассона
Пусть производится n независимых испытаний в каждом из которых вероятность появления события A равна p. Для определения вероятности k появлений события в этих испытаниях используют формулу Бернулли. Если же n велико, то пользуются асимптотической формулой Лапласа (см. Лабораторную работу № 3). Однако эта формула не пригодна, если вероятность события мала (npq<9). В этих случаях прибегают к асимптотической формуле Пуассона.
Данное распределение в лабораторной работе №4 не будет рассматриваться, так как возможности математического пакета Maple позволяют рассчитывать вероятность непосредственно по формуле Бернулли при ОЧЕНЬ больших n и при ОЧЕНЬ малых p, как собственно и стандартный калькулятор встроенный в программу Windows. А расчеты по прямой формуле имеют гораздо меньшую погрешность, а значит и большую ценность, чем по асимптотическим. Данный вопрос вынесен на практические занятия.
Геометрическое распределение
Пусть производятся независимые испытаний, в каждом из которых вероятность появления события A равна p (0<p<1) и, следовательно, вероятность его непоявления Испытания заканчиваются как только появляется событие A. Таким образом, если событие A появилось на k-м испытании, то в предшествующих k-1 испытаниях оно не появлялось.
Обозначим через Х дискретную случайную величину – число испытаний, которое нужно провести до первого появления события A. Возможные значения X – весь натуральный ряд. Вероятность рассчитывается по формуле:
Таблица №2
| Математическое ожидание | |
| Дисперсия |
Задача №2.
Из орудия производится стрельба до первого попадания. Вероятность попадания в цель X – дискретная случайная величина числа испытаний. Составить таблицу (матрицу) распределения для X=1,2,…10. Найти по формулам (1) и (2) математическое ожидание и дисперсию. Подтвердить полученные результаты по формулам из таблицы №2. Найти среднее квадратическое отклонение. Сколько раз надо сделать выстрелов, чтобы с вероятностью 0,999 попасть по мишени?
Решение:
Вероятность будет рассчитываться по формуле:
> 

Составим первые 10 столбцов таблицы (матрицы) распределения. Очевидно, что вся таблица – бесконечна.
> 

Убедимся, что сумма всех вероятностей во второй строке распределения равна 1, для этого составим ряд:
> 

Найдем математическое ожидание:
> 

По формуле: результат подтверждается.
Найдем дисперсию:
> 

D=0.56
По формуле: результат подтверждается.
Найдем среднее квадратическое отклонение:
> 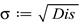

> 

Ответим на вопрос сколько раз надо сделать выстрелов, чтобы с вероятностью 0,999 попасть по мишени
> 

Вызовом контекстного меню, решаем данное неравенство:
> 

Итак, уже при шести выстрелах, вероятность поражения хотя бы один раз мишень достигнет 0,999.