(выдается каждому студенту)
Подготовка к работе.
Домашнее задание на повторение необходимого для выполнения работы теоретического материала.
Литература для повторения:
1. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. М. 1968.
2. Федорчук В.В. Курс аналитической геометрии и линейной алгебры: Учеб. пособие.- М.: Изд-во МГУ, 1990.
При подготовке необходимо уяснить для себя смысл следующих понятий и утверждений, а также возможности их использования:_
1.Уравнения множества точек (геометрической фигуры), в частности уравнения линии (1,гл.4,§1.п.1,2, с. 92-94,п. 4, с.97);
2. Условие коллинеарности двух векторов (1, гл.2,§1.п.1,с.47,п.2, с.52, т.2.1, п.4,с. 54, т.2.4.; 2, гл.1, § 8,с.27);
3. Условие принадлежности трех точек одной прямой (2, гл.2, §14, с.47), вытекающее из условия коллинеарности двух векторов;
4. Условие перпендикулярности двух векторов (1, гл.2,§2.п.1, т. 2.10 с.66);
5. Способы задания прямой линии на плоскости и в пространстве(вспомнить школьный курс геометрии)
Непосредственно лабораторной работы касается содержание параграфов: [1], гл.5,§1.п.1–5, §2.п.1; [2], гл.2, §14,с.47-50.
Лабораторная работа
Тема: Различные уравнения прямой линии на плоскости и в пространстве
Цели: 1. Рассматривая разные способы задания прямой, получить всевозможные уравнения прямой в двух ситуациях: а) прямая лежит в плоскости, б) прямая расположена в пространстве;
2. Запомнить все уравнения прямой линии на плоскости и в пространстве и геометрический смысл параметров каждого уравнения;
3. Уметь составить уравнение прямой по элементам, которые эту прямую однозначно определяют;
4. Научиться докладывать и оценивать результаты своей работы.Выполнение лабораторной работы основано на следующей опорной базе теоретических знаний.
1. Понятие характеристического свойства точек заданной геометрической фигуры.
Характеристическим свойством точек геометрической фигуры называют то свойство, которому удовлетворяют точки данной фигуры и не удовлетворяют точки плоскости (пространства), которые ей не принадлежат. Так например, характеристическим свойством точек окружности является их удаленность от центра на одно и тоже расстояние.
2. Определение уравнения геометрической фигуры:
а) в некоторой системе координат,
б) в инвариантной, векторной, форме.
Напомним оба эти понятия.
Уравнением (уравнениями) множества точек на плоскости относительно заданной системы координатназывается уравнение (или система уравнений, а также неравенство или система неравенств), которому (которым) удовлетворяют координаты любой точки данного множества и не удовлетворяют координаты точек, этому множеству не принадлежащих.
Согласно определению уравнение прямой линии должно связывать координаты (x,y) произвольной точки прямой с координатами точек или векторов, которые эту прямую определяют.
Векторным уравнением множества точек на плоскости или в пространстве называется уравнение, связывающее радиус-векторы точек заданного множества, которому не удовлетворяют радиус-векторы точек, не принадлежащих этому множеству.
Понятие уравнения пространственной геометрической фигуры относительно заданной системы координат ничем не отличается от сформулированного.
3. Условие коллинеарности двух векторов.
Векторы называются коллинеарными, если они лежат на одной прямой, либо на параллельных прямых.
Необходимое и достаточное условие коллинеарности двух векторов выражено в следующей теореме:
Теорема. Вектор b коллинеарен ненулевому вектору a тогда и только тогда, когда существует вещественное число l такое, что b = l a.
4. Условие принадлежности трех точек одной прямой вытекат из
условия коллинеарности двух векторов.
Точки А, В, С принадлежат одной прямой тогда и только тогда, когда векторы 
и 
коллинеарны, то есть когда существует вещественное число l такое что 
.
5. Способы задания прямой линии на плоскости.
Дадим некоторые определения.
Определение. Любой ненулевой вектор, параллельный заданной прямой, называется направляющим вектором этой прямой.
Определение. Любой ненулевой вектор, перпендикулярный заданной прямой, называется нормальным вектором этой прямой.
Из школьного курса известно, что
1. Через две точки проходит единственная прямая;
2. Через точку, лежащую вне прямой можно провести прямую и притом только одну.
3. Через точку в плоскости можно провести только один перпендикуляр к данной прямой.
Из этих утверждений вытекают три способа задания прямой линии на плоскости.
1. Точкой и направляющим вектором (см. рис.1);
2. Двумя точками (см. рис.2);
3. Точкой и нормальным вектором (см. рис.3).
Ход выполнения работы
1.Вывод уравнения прямой, заданной точкой и направляющим вектором
1. Сделайте рисунок, соответствующий рассматриваемому заданию прямой, обозначьте заданную точку символом А, а направляющий вектор символом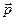 
.
2. Выделите характеристическое свойство точек прямой, проходящей через точку А и имеющей направляющим вектор .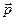
3. Запишите это условие в виде векторного уравнения.
4. Выразите из полученного уравнения радиус-вектор текущей (произвольной) точки этой прямой.
Полученное уравнение называется векторным параметрическим
уравнением прямой по точке и направляющему вектору, занумеруйте его числом (1).
Роль числа – параметра, входящего в уравнение прямой, состоит в том, что оно определяет положение точки на прямой: каждому значению этого параметра соответствует единственная точка на прямой и наоборот, каждой точке прямой соответствует вполне определенное число.
5. Запишите уравнение (1) в координатной форме. Для этого задайте точку А, текущую точку прямой и направляющий вектор 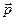координатами в некоторой (выбранной Вами) системе координат.
Полученные уравнения называются параметрическими уравнениями прямой на плоскости по точке и направляющему вектору в координатной форме. З анумеруйте их числом (2).
6. Исключите из параметрических уравнений (2) параметр. Получите уравнение, которое называется каноническим уравнением прямой на плоскости. Поставьте емув соответствие номер ( 3).
7. Приведите уравнение ( 3) к виду Ax + By + C = 0, используя свойство пропорции и переобозначение коэффициентов. Убедитесь, что в уравнении
Ax + By + C = 0 (4)
коэффициенты A и B не равны 0 одновременно.
Докажите, что всякое линейное уравнение (4), в котором коэффициенты A и B не равны 0 одновременно, является уравнением прямой линии в некоторой системе координат (см. 2, с.45 или 1, с. 110).
8. подумайте с сформулируйте геометрический смысл коэффициентов при переменных в уравнении (4).
Уравнение (4) называется общим уравнением прямой на плоскости.
9. Выразите из уравнения (4) переменную y и получите уравнение вида
y = kx + b (5)
Такое уравнение называется уравнением прямой с угловым коэффициентом
10. Приведите уравнение (4) к виду
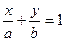(6)
При каких условиях оно может быть приведено к этому виду? Выясните, каков геометрический смысл параметров 
этого уравнения, найдя пересечение прямой (6) с осями координат.
Уравнение (6) называется уравнением прямой в отрезках. Объясните почему.
11. Вывод уравнения прямой по двум точкам
1. Сделайте рисунок, иллюстрирующий задание прямой двумя точками.
2. Сведите этот способ задания к предыдущему, найдя направляющий вектор заданной прямой.
3. Запишите уравнения вида (1), (2) и (3) в этом случае.
Они будут соответственно называться:
а) векторным параметрическим уравнением прямой по двум точкам на плоскости (7),
б) параметрическими уравнениями прямой на плоскости по двум точкам в координатной форме (8),
в) каноническим уравнением прямой на плоскости по двум
точкам (9).
111. Вывод уравнения прямой на плоскости по точке и нормальному вектору.
1. Сделайте рисунок, иллюстрирующий задание прямой в этом случае, обозначив заданную точку символом А, а нормальный вектор символом 
.
2. Выделите характеристическое свойство точек прямой, проходящей через точку А перпендикулярно вектору .
3. Запишите это условие в виде векторного уравнения.
4. Выбрав прямоугольную декартову систему координат и задав в ней координаты точки А, текущей точки прямой и нормального вектора к этой прямой, запишите полученное в пункте 3 уравнение в координатной форме. Получите уравнение
, (10)
которое называется уравнениями прямой на плоскости по точке и нормальному вектору.
1V. Вывод уравнений прямой линии в пространстве
1. Выясните, какие из рассмотренных способов задания прямой на плоскости годятся и для задания прямой в пространстве.
2. Выпишите соответствующие этим способам параметрические и канонические уравнения для прямой в пространстве.
V. По результатам проведенного исследования заполните следующую таблицу.