Фигура Земли с учетом данных Добрецова Н.Л.[3] о распределении плотности.
Пусть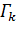 
(к=1,2,…n)-поверхность раздела слоев с разной плотностью 
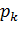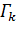, –свободная поверхность Земли. (Рисунок 1)
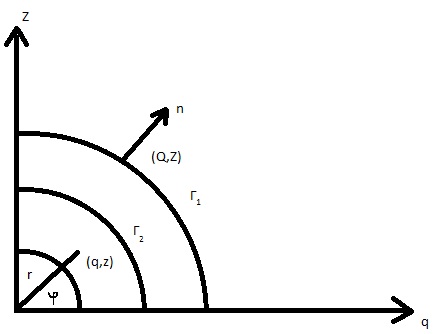
Рисунок 1- Слоистая структура Земли.
Гравитационный потенциал с учетом инерции вращения вокруг оси Z c угловой скоростью ω равен:
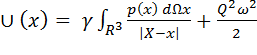. (3.1)
Здесь
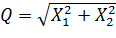, Z=X3, 
.
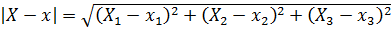Вектор силы ускорения свободного падения F=∇U,
Уравнение Свободной поверхности раздела: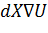 
=0,
Сделаем замену переменных интегрирования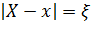 
и подставим в (3.1),
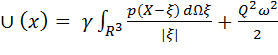, (3.2)
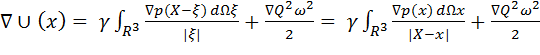. (3.3)
Для кусочно-постоянного распределения плотности
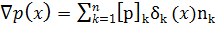. (3.4)
где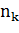 
-вектор внешней нормали к , 
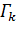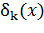-Функция Дирака на , 
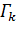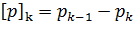-скачок плотности. Эта формула вытекает из геометрического смысла градиента – направление наибольшего роста функции (при наличии производных, а в данном случае направление градиента получается предельным переходом с помощью последовательности сглаженных функций). Подставим (3.4) в (3.3).
Таким образом
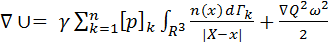. (3.5)
Численная реализация
В плоскости (q,z):
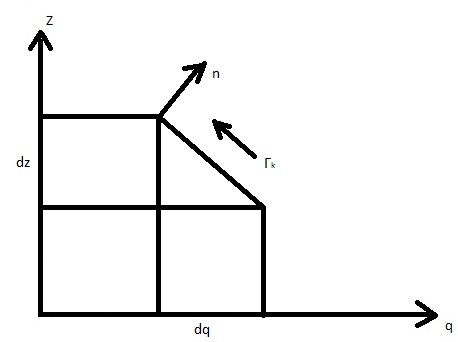
Рисунок 2- Элемент границы раздела.
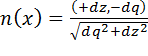, (4.1)
. (4.2)
В пространственных осях
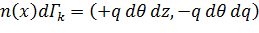, (4.3)
Распишем (4.3)
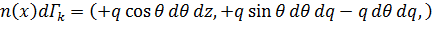, (4.4)
При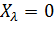 
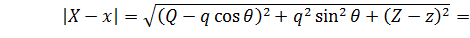
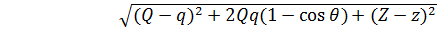. (4.5)
Введем интегралы:
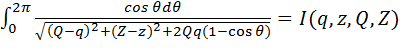, (4.6)
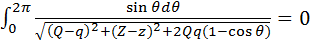, (4.7)
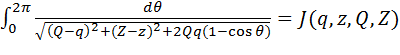, (4.8)
Тогда получим:
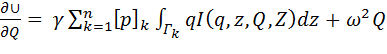, (4.9)
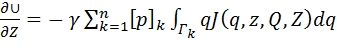. (4.10)
Уравнение границы разделения 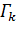имеет вид:
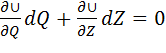. (4.11)
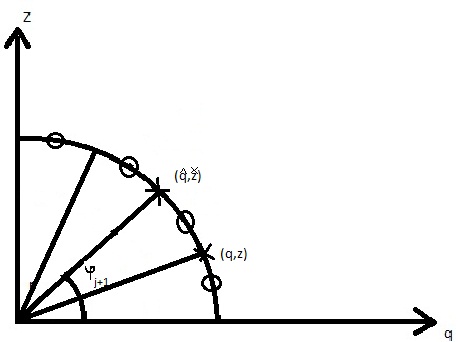
Рисунок 3- Полярная Сетка.
Аппроксимация на полярной сетке уравнение (4.11):
, (4.12)
, (4.13)
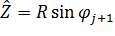. (4.14)
Вставим в формулу (4.12) значения 
из (4.13) и (4.14), а затем выразим R.
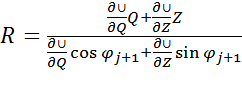. (4.15)
Для того, чтобы вычислить интегралы в формулах (4.9)-(4.10), рассмотрим эллиптический интегралы:
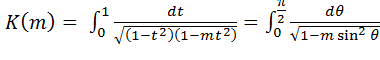, (4.16)
(4.16)-эллиптический интеграл первого рода,
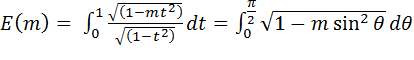, (4.17)
(4.17)-эллиптический интеграл второго рода,
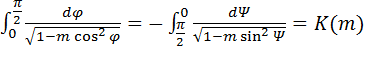, (4.18)
.
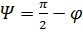Здесь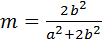 
. Получим:
 ,
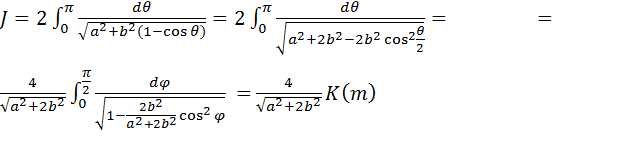| (4.19) |
 ,
| 
|
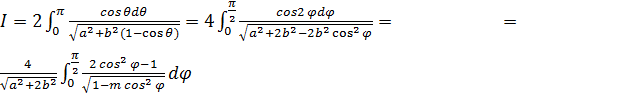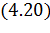
Разложим подынтегральное выражение на простые дроби:
 ,
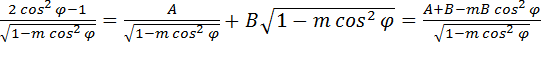| (4.21) |
, 
, 
, 
,
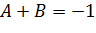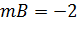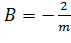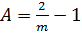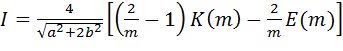. (4.22)
Для вычисления интегралов использовалась следующая формула Гаусса с двумя узлами:
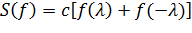, (4.23)
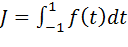. (4.24)
Входящие сюда коэффициенты определяются из условия совпадения точных и приближенных совпадений интегралов от степенных функций в соответствии с таблицей 7.
Таблица 7.
| 
| 
|
| 
| 
|
| 
|
|
| 
| 
|
|
|
|
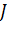
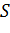
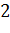
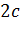
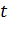
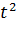
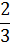
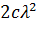
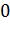
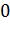
Точна для многочленов третей степени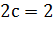 
, 
, 
, 
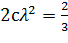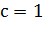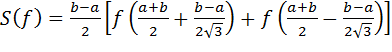. (4.23)
Результаты расчетов
Программные вычисления показали, что фигура Земли в первом приближении представляет собой эллипсоид вращения, у которого экваториальный радиус (а) больше полярного (b) на 21,666 км (рисунок 4) по справочным данным [5]. С учетом распределения по данным Добрецова- 22,946 км. По данным Гамильтона 23,244 км. По данным Буллену-Хаддону 20,745 км. По данным Гутенбергу-Буллену 22,585. По данным Мельхиору 23,271. По данным Современной модели Земли 20,366
Значение g полученное программой для всех справочных данных оказалось практически одинаковым (рисунок 5).
Рисунок 4- Эллипсоид.
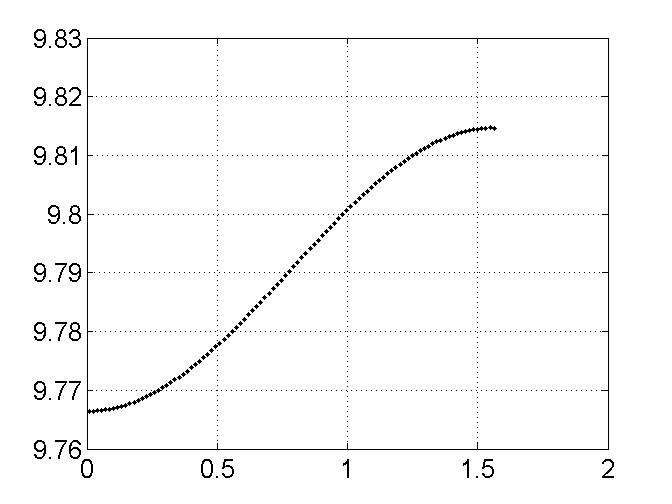
Рисунок 5- Ускорение свободного падения в зависимости от широты.
ЗАКЛЮЧЕНИЕ
В магистерской работе разработан вычислительный алгоритм и программа в системе Matlab для расчета фигуры вращающейся Земли на основе данных о слоистой распределении плотности. Проведены расчеты для известных моделей слоистой Земли, результаты которых по геометрическим параметрам оказались близкими к параметрам эллипсоида Красовского.