Дифракция света.
Цель работы: наблюдение дифракционных картин от щели, от объекта
с хаотичным расположение рассеивающих частиц,
от дифракционной решетки; расчет основных параметров
объектов и применяемого излучения по дифракционным
картинам.
Введение.
Первое упоминание о дифракционных явлениях появилось ещё в работе Леонардо да Винчи в 1502 году. Однако, впервые они были описаны детально в книге Гримальди, опубликованной в 1665 году спустя два года после его смерти. Вопросами дифракции света занимались Роберт Гук, Томас Юнг, Исаак Ньютон. Корпускулярная теория, которую считали в то время правильно описывающей распространение света, не могла объяснить дифракцию. О возможности объяснить дифракцию с волновых позиций нигде не упоминалось вплоть до 1818 года, когда появился прекрасный "Мемуар о дифракции света" Огюстена Жака Френеля, где было показано, что явления дифракции можно объяснить с помощью построений Гюйгенса и применяя принцип интерференции. Позднее Кирхгоф (1882) придал исследованиям Френеля строгое математическое обоснование, и с этого времени началось широкое изучение дифракции.
Проблемы, возникающие при изучении дифракционных явлений относятся к наиболее трудным в оптике, и их редко удается довести до строгого решения. Первое такое решение было получено только в 1896 году Зоммерфельдом. С тех пор было найдено строгое решение только нескольких задач, относящихся главным образом к двумерным структурам.
В большинстве же случаев, представляющих практический интерес, из-за математических трудностей приходится прибегать к приближенным методам, и тут теория Гюйгенса и Френеля служит чрезвычайно мощным орудием, позволяющим решить большинство вопросов, встречающихся в инструментальной оптике.
Согласно построению Гюйгенса каждую точку волнового фронта можно считать центром вторичного возмущения, которое вызывает элементарные вторичные сферические волны.
Френель смог объяснить дифракцию, дополнив построения Гюйгенса утверждением, что вторичные волны интерферируют между собой.
Различают дифракцию Френеля и дифракцию Фраунгофера. Их различие определяется положением точки наблюдения по отношению к объекту, на котором происходит дифракция и видом волны, падающей на объект.
В 1821 году Фраунгофер рассмотрел несколько другой тип дифракции, чем дифракция Френеля - дифракция сферической волны на конечных расстояниях до объекта. Он использовал плоскую волну, которую легко получить, поместив точечный источник в фокусе собирающей линзы. Помещая, затем, различные объекты на пути плоской волны можно наблюдать различные дифракционные эффекты. Важность фраунгоферовой дифракции велика. Она находит широкое применение в оптических приборах, а с момента изобретения лазерных источников, стала основной.
Рассмотрим дифракционные эффекты, возникающие при прохождении плоской световой волны через щель.
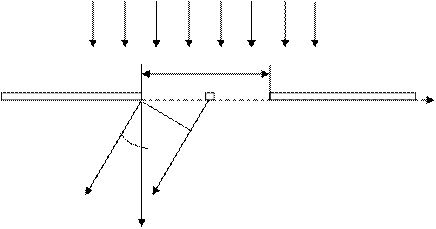
Пусть щель шириной b освещается монохроматическим светом с длиной волны λ (рис.1). Фронт волны плоский, т.е. имеет место дифракция Фраунгофера.
Eo
b
x dx X
Δ
φ
dEφ
Z
Рис. 1
Ось х направлена вдоль ширины щели. Ось z перпендикулярно плоскости щели. Пусть элемент волны dx, находящийся во фронте волны и дошедший до плоскости щели, становится источником вторичных волн. Рассмотрим амплитуду волны, излучаемую в направлении φ. Тогда dE = Cdx, где С - коэффициент пропорциональности не зависящий от φ. Суммарная амплитуда от всей щели Eo запишется, как
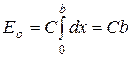, тогда 
.
В направлении φ элемент фронта волны пошлет амплитуду
.
Просуммируем элементарные вторичные волны от элемента dx по направлению φ по всей щели.
Умножив числитель и знаменатель на 
и применив формулу Эйлера, получим
Временной множитель не влияет на распределение интенсивности в пространстве, и поэтому перейдем к интенсивности, учитывая, что Iφ = Eφ Eφ*, окончательно получим
.
Исследуем это уравнение распределения интенсивности в направлении φ.
Если φ = 0, то I = Io.
Если φ ≠ 0, то нулю все же может равняться числитель при других условиях. Этому условию удовлетворяет уравнение 
- минимумы дифракции.
Рис. 2
На рис. 2 представлено графически распределение относительной интенсивности при дифракции на щели. Максимумы этой функции очень малы. Если принять Io = 1000, то I1 = 47, I2 = 17 и т.д.
Ширину дифракционного нулевого максимума при малом φ можно записать
,
т.е. при увеличении размера щели ширина максимума уменьшается и, наоборот, при уменьшении - увеличивается.
Рассмотрим теперь дифракцию Фраунгофера при падении плоской волны на отверстие произвольной формы. В отличие от щели здесь волны дифрагируют во всех направлениях. Каждое направление дифрагировавших волн характеризуется единичным вектором s (рис. 3).
x
s
dS s
r
0 z
y
Рис. 3
Пусть отверстие лежит в плоскости xy. Разность хода идущих по направлению s вторичных волн из элемента dS этого отверстия и из начала координат О равна проекции вектора r, определяющего положение dS в плоскости xy, на направление s, т.е. r s. В соответствии с принципом Гюйгенса-Френеля напряженность электрического поля световой волны в направлении s пропорциональна интегралу по всей площади отверстия:
где k = k s - волновой вектор светового излучения. Напряженность Е( r ) в плоскости xy считается равной напряженности поля падающей волны в пределах отверстия и равной нулю за его пределами. Понимая функцию Е(x,y) именно так, можно распространить интегрирование на всю плоскость xy:
.
Отсюда видно, что поле в фраунгоферовой дифракционной картине представляет собой двумерное преобразование Фурье функции Е(x,y), описывающей поле в плоскости xy.
Большой практический интерес представляет дифракция на круглом отверстии, так как в оптических приборах оправы линз и объективов, а также диафрагмы имеют обычно круглую форму. При вычислении двумерного интеграла целесообразно перейти к полярным координатам ρ и φ в плоскости отверстия: x = ρ cos (φ), y = ρ sin (φ). Направление s дифрагировавшей волны, удобно характеризовать углом θ с осью z и азимутальным углом ψ: kx = ksin θ cos ψ, ky = ksin θ sin ψ. Тогда kx + ky =
= k ρ sin θ cos( φ - ψ) и интеграл для напряженности поля примет вид
Здесь а - радиус отверстия. Используя интегральное представление для бесселевых функций, вычислим этот интеграл. Результат даст следующее радиальное распределение интенсивности в дифракционной картине:
График этой функции очень похож на график интенсивности рассеяния от щели. Функция имеет главный максимум при u = 0 и с ростом u осциллирует с быстрым уменьшением амплитуды. Угловые радиусы темных колец равны 0,61λ/а; 1,12λ/а; 1,62λ/а; 2,12λ/а …. Эффективный размер дифракционной картины здесь обратно пропорционален размеру отверстия. Интенсивность максимумов быстро уменьшается. Поэтому центральный максимум, имеющий угловой радиус θ = 0,61λ/а, можно рассматривать как изображение точечного источника, уширенное дифракцией на круглом отверстии радиусом а. Соотношение играет важную роль в вопросе о разрешающей силе оптических инструментов.
Особый интерес представляет случай, когда в экране имеется большое число одинаковых, круглых отверстий. При хаотическом, беспорядочном, расположении отверстий фазовые соотношения между волнами от отдельных отверстий имеют случайный характер. Поэтому для каждого направления наблюдения происходит простое сложение интенсивностей волн, дифрагировавших от всех отверстий. Распределение интенсивности в дифракционной картине от одного отверстия не зависит от его положения. От большого числа N отверстий получается такая же картина, но усиленная по интенсивности в N раз.
При правильном, регулярном расположении отверстий, когда их ориентация и расстояния между ними одинаковы, разность фаз между дифрагировавшими волнами имеет определенное значение. В направлениях, для которых разность фаз кратна 2π, амплитуда дифрагировавших волн в N раз больше, а интенсивность в N 2 раз больше чем от одного отверстия. Такое резкое увеличение интенсивности имеет большое практическое применение.
Случай регулярного расположения отверстий рассмотрим на примере дифракционной решетки.
Пусть имеем правильную структуру из N щелей (рис. 4). От элемента dx n- ой щели распространяется элементарная волна dEφ.
Вся n - ая щель пошлет волну в виде
Eo
d
b x dx x
 |
φ Δ
z dEnφ
Рис. 4
Интеграл нам уже знаком тем, что он представляет дифракцию от одной щели, в этом случае
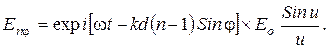
Для нахождения действия всех щелей необходимо просуммировать амплитуды от каждой щели по N щелям.
Член 
не зависит от n, тогда его выносим за знак суммы и, обозначив 
, получим следующее выражение
.
Сумма представляет собой геометрическую прогрессию со знаменателем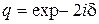 
. Учитывая это и, что I = E·E*, окончательно получаем
,
где 
Множитель Sin2u/u2 характеризует распределение интенсивности в результате дифракции плоской волны на одной щели, а множитель
(Sin Nδ/Sin δ)2 учитывает интерференцию между пучками, исходящими от всех щелей. На рис. 5 представлен график распределения интенсивности в дифракционной картине от решетки из пяти щелей, причем соотношение d/b=5. Штриховой линией изображен график функции без учета действия щели, т.е. I/Io = (Sin Nδ/Sin δ)2.
Анализ полученных результатов позволяет сделать ряд важных выводов. При нулевом значении угла φ=0 относительная интенсивность пропорциональна N2. Такие же значения получаются для случая, если πd/λ·Sinφ=mλ, где m = ± 1, 2, 3, …. Это есть ни что иное, как условие положения дифракционных максимумов, которое принято записывать в виде
- формула дифракционной решетки.
Однако, если учитывать и первый член в уравнении интенсивности рассеяния, т.е. множитель обусловленный действием щели, то вид дифракционной картины изменяется. Дифракционные максимумы изменяются в интенсивности и наблюдаются только при таких углах, при которых оба члена уравнения не нулевые.
Для того чтобы выяснить условие минимумов следует обратить числитель уравнения интенсивности в нуль, при не нулевом знаменателе. Это возможно при 
или 
, где k = ± 1,2,3,…. В этом случае k/N ≠ m, так как m входит в выражение знаменателя уравнения
Рис. 5
интенсивности и обнуляет его. Необходимо исключит это условие. Такое возможно при k ≠ 0, k ≠ N, k ≠ 2N и т.д., другими словами - между двумя главными максимумами будет находится (N – 1) минимум. Минимумы будут разделятся (N – 2) побочными максимумами, интенсивность которых очень мала.
Анализ, проведенный выше, предполагал, что λ = const. Если на решетку будет падать белый свет, то из условия видим, что для различных длин волн углы дифракции будут различны и чем больше длина волны, тем больше угол дифракции при постоянном периоде решетки. Таким образом, все максимумы, кроме центрального, разложатся в спектр. При больших порядках дифракции возможно перекрывание спектров соседних порядков. Это свойство дифракции, дисперсию, стали использовать в спектральных исследованиях.
Угловая дисперсия - это характеристика дифракционной решетки как спектрального дисперсионного прибора. Она выражается соотношением
,
и показывает, на какое угловое расстояние разойдутся две спектральные линии, отличающиеся на δλ. Чтобы найти угловую дисперсию дифракционной решетки из её параметров возьмем полный дифференциал от формулы решетки
.
Из полученного выражения следует, что угловая дисперсия обратно пропорциональна периоду решетки и прямо пропорциональна порядку дифракционного максимума.
Описание экспериментальной установки.
В работе используется распространенная в лабораторной практике решетка, представляющая собой стеклянную или пластиковую пластинку, на которую с помощью делительной машины специальным алмазным резцом нанесен ряд параллельных штрихов.
Для измерения угла отклонения применяется гониометр Г-5. Источником исследуемого излучения является ртутная лампа.
При исследовании дифракции на щели и хаотично расположенных круглых частичках одинакового размера применяется в качестве источника гелий неоновый лазер. Рассеянное объектом излучение лазера фиксируется коллимированным фотоприемником, установленным на препаратоводителе и позволяющим отсчитывать линейное перемещение фотоприемника с точностью 0,5 мм.