Домашние контрольные работы (ААб, математика)
Индивидуальные задания № 1
(Глава 1. Элементы линейной алгебры)
ЗАДАНИЕ 1.
Решить заданную систему методами Крамера, Гаусса, обратной матрицы. Выполнить проверку полученного решения.


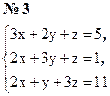

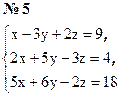
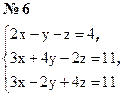












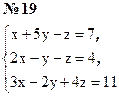
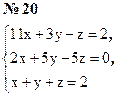










Индивидуальные задания № 2
(Глава 2. Векторная алгебра)
ЗАДАНИЕ 1.
Заданы координаты вершин пирамиды АВСD. Требуется:
1) Записать векторы  в системе орт
в системе орт  ;
;
2) Найти периметр треугольника BCD.
3) Найти угол между векторами  ;
;
4) Найти проекцию вектора  на вектор
на вектор  ;
;
5) Найти площадь грани АВС;
6) Найти объем пирамиды АВСD;
7) Найти длину высоты DH пирамиды, опущенной из вершины D на основание АВС.
№1. А(2;-3;1), B(6;1;-1), C(4;8;-9), D(2;-1;2)
№2. A(5;-1;-4), B(9;3;-6), C(7;10;-14), D(5;1;-3)
№3. A(1;-4;0), B(5;0;-2), C(3;7;-10), D(1;-2;1)
№4. A(-3;-6;2), B(1;-2;0), C(-1;5;-8), D(-3;-4;3)
№5. A(-1;1;-5), B(3;5;-7), C(1;12;-15), D(-1;3;-4)
№6. A(1;2;1), B(-1;5;1), C(-1;2;7), D(1;5;9)
№7. A(2;3;2), B(0;6;2), C(0;3;8), D(2;6;10)
№8. A(0;3;2), B(-2;6;2), C(-2;3;8), D(0;6;10)
№9. A(2;1;2), B(0;4;2), C(0;1;8), D(2;4;10)
№10. A(2;3;0), B(0;6;0), C(0;3;6), D(2;6;8)
№11. A(2;2;1), B(0;5;1), C(0;2;7), D(2;5;9)
№12. A(1;3;1), B(-1;6;1), C(-1;3;7), D(1;6;9)
№13. A(1;2;2), B(-1;5;2), C(-1;2;8), D(1;5;10)
№14. A(2;3;1), B(0;6;1), C(0;3;7), D(2;6;9)
№15. A(2;2;2), B(0;5;2), C(0;2;8), D(2;5;10)
№16. A(1;3;2), B(-1;6;2), C(-1;3;8), D(1;6;10)
№17. A(0;1;2), B(-2;4;2), C(-2;1;8), D(0;4;10)
№18. A(0;3;0), B(-2;6;0), C(-2;3;6), D(0;6;8)
№19. A(2;1;0), B(0;4;0), C(0;1;6), D(2;4;8)
№20. A(0;2;1), B(-2;5;1), C(-2;2;7), D(0;5;9)
№21. A(1;1;1), B(-1;4;1), C(-1;1;7), D(1;4;9)
№22. A(1;2;0), B(-1;5;0), C(-1;2;6), D(1;5;8)
№23. A(0;1;0), B(-2;4;0), C(-2;1;6), D(0;4;8)
№24. A(0;1;1), B(-2;4;1), C(-2;1;7), D(0;4;9)
№25. A(0;2;0), B(-2;5;0), C(-2;2;6), D(0;5;8)
№26. A(1;3;2), B(-1;4;3), C(-1;2;7), D(1;4;9)
№27. A(2;1;2), B(0;4;2), C(-1;3;4), D(2;0;8)
№28. A(1;2;1), B(-2;3;4), C(0;1;3), D(1;3;8)
№29. A(2;2;2), B(-1;6;2), C(-2;3;4), D(2;6;9)
№30. A(1;3;1), B(-2;5;1), C(-1;2;6), D(1;5;10)
Индивидуальные задания № 3
(Глава 3. Аналитическая геометрия на плоскости)
ЗАДАНИЕ 1. (Прямая линия на плоскости)
Даны координаты вершин треугольника АВС. Найти:
1) Длину стороны АВ;
2) Уравнения сторон АВ и ВС и их угловые коэффициенты;
3) Внутренний угол В;
4) Уравнение медианы АЕ;
5) Уравнение и длину высоты СD;
6) Уравнение прямой, проходящей через точку Е параллельно стороне АВ и точку М ее пересечения с высотой СD.
№1. A(1;-1), B(4;3), C(5;1)
№2. A(0;-1), B(3;3), C(4;1)
№3. A(1;-2), B(4;2), C(5;0)
№4. A(2;-2), B(5;2), C(6;0)
№5. A(0;0), B(3;4), C(4;2)
№6. A(0;1), B(3;5), C(4;3)
№7. A(3;-2), B(6;2), C(7;0)
№8. A(3;-3), B(6;1), C(7;-1)
№9. A(-1;1), B(2;5), C(3;3)
№10. A(3;-3), B(6;1), C(7;-1)
№11. A(2;2), B(5;6), C(6;4)
№12. A(4;-2), B(7;2), C(8;0)
№13. A(0;2), B(3;6), C(4;4)
№14. A(4;1), B(7;5), C(8;3)
№15. A(3;2), B(6;6), C(7;4)
№16. A(-2;1), B(1;5), C(2;3)
№17. A(4;-3), B(7;1), C(8;-1)
№18. A(-2;2), B(1;6), C(2;4)
№19. A(5;0), B(8;4), C(9;2)
№20. A(2;3), B(5;7), C(6;5)
№21. A(-3;0), B(1;3), C(-2;-2)
№22. A(-4;1), B(0;4), C(1;0)
№23. A(-3;-2), B(0;2), C(-2;-2)
№24. A(-4;-1), B(-1;3), C(2;0)
№25. A(-5;-2), B(-1;1), C(0;4)
№26. A(-8;-3), B(4;-12), C(8;10)
№27. A(-5;7), B(7;-2), C(11;20)
№28. A(-12;-1), B(0;-10), C(4;12)
№29. A(-10;9), B(2;0), C(6;22)
№30. A(0;2), B(12;-7), C(16;15)
ЗАДАНИЕ 2. ( Кривые второго порядка)
Привести уравнение кривой второго порядка к каноническому виду, определить геометрический образ и построить кривую.
№1. а) x2 – 10x+y2 + 4y + 4 = 0; б) 2x2 + 5y2 – 12x – 10y+ 9 =0;
в) 2x2 – y2 – 8x – 2y – 1 = 0; г)  .
.
№2. а) x2 + y2 + 4x – 60 = 0; б) 4x2 + 25y2 – 24x + 350y + 61 = 0;
в) 16x2 – 9y2 – 64x – 54y – 161 = 0; г) 4x2 – 8x – y – 7 = 0.
№3. а) x2 – 10x + y2 + 4y – 20 = 0; б) 4x2 + 9y2 + 8x – 18y + 12 = 0;
в) x2 – 16y2 – 4x + 32y – 28 = 0; г) 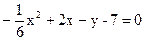 .
.
№4. а) x2 + y2 – 10x + 20 = 0; б) x2 + 4y2 + 4x – 16y – 18 = 0;
в) 2x2 – 6y2 + 12x – 12y = 0; г) 2y2 – x – 12y + 14 = 0.
№5. а) x2 + y2 – 2x + 4y + 14 = 0; б) 9x2 + 25y2 + 18x + 10y – 164 = 0;
в) 3x2 – 2y2 – 6x + 4y – 7 = 0; г)  .
.
№6. а) x2 + y2 – 2x + 4y + 14 = 0; б) 16x2 + 9y2 + 96x – 18y + 56 = 0;
в) 16x2 – 9y2 – 64x – 54y – 162 = 0; г) –y2 – x – 2y – 1 = 0.
№7. а) x2 + y2 + 4x – 2y + 5 = 0; б) 4x2 + 16y2 + 96y + 80 = 0;
в) 9x2 – 16y2 + 90x + 32y – 367 = 0; г)  .
.
№8. а) x2 + y2 + 6x – 4y + 14=0; б) 5x2 + 2y2 – 10x – 14y – 3 = 0;
в) 16x2 – 9y2 – 64x – 18y + 199 = 0; г) y2 – 16x – 6y + 25 = 0.
№9. а) x2 + y2 – 4x+ 6y = 0; б) 4x2 + y2 – 4x + 6y + 4 = 0;
в) 16x2 – 9y2 – 64x – 18y + 199 = 0; г) x2 + 8x – 9y – 29 = 0.
№10. а) x2 + y2 + 5x + 2y – 1 = 0; б) 2x2 + 5y2 + 8x – 10y – 17 = 0;
в) x2 – 6y2 – 12x + 36y – 48 = 0; г) x2 – 4x + 2y – 2 = 0.
№11. а) x2 – y2 – 2x + 4y – 4 = 0; б) 5x2 + 2y2 – 10x – 12y + 9 = 0;
в) – x2 + 2y2 – 2x – 8y – 1 = 0; г)  .
.
№12. а) x2 + y2 – 4x + 2y + 1 = 0; б) 25x2 + 4y2 + 350x – 24y + 57 = 0;
в) 9x2 – 16y2 + 54x + 64y + 161 = 0; г) 4y2 – x – 8y – 7 = 0.
№13. а) 2x2 + 2y2 + 5x – 3y – 2 = 0; б) 9x2 + 4y2 – 18x + 8y + 12 = 0;
в) 16x2 – y2 – 32x – 4y + 28 = 0; г)  .
.
№14. а) x2 + y2 – 6x – 7 = 0; б) 4x2 + y2 – 16x + 4y – 18 = 0;
в) 6x2 – 2y2 + 12x – 12y = 0; г) 2x2 – 12x – y + 14 = 0.
№15. а) x2 + y2 + 3y = 0; б) 25x2 + 9y2 + 100x + 18y – 164 = 0;
в) 2x2 – 3y2 + 4x + 6y + 7 = 0; г)  .
.
№16. а) x2 + y2 + 4x – 2y + 14 = 0; б) 9x2 + 16y2 – 18x + 96y + 56 = 0;
в) 9x2 – 16y2 + 54x + 64y + 161 = 0; г) – y2 – x – 2y – 1 = 0.
№17. а) x2 + y2 – 2x + 4y – 20 = 0; б) 16x2 + 4y2 + 96x + 80 = 0;
в) 16x2 – 9y2 – 32x – 90y – 367 = 0; г)  .
.
№18. а) x2 + y2 – 4x + 6y – 12 = 0; б) 2x2 + 5y2 – 4x – 10y – 3 = 0;
в) 9x2 – 16y2 + 18x + 64y + 199 = 0; г) x2 – 6x – 16y + 25 = 0.
№19. а) x2 + y2 + 6x + 4y = 0; б) x2 + 4y2 + 6x – 4y + 4 = 0;
в) 9x2 – 16y2 + 18x + 64y + 199 = 0; г) y2 – 9x + 8y – 29 = 0.
№20. а) x2 + y2 + 2x + 5y – 1 = 0; б) 5x2 + 2y2 – 10x + 8y – 17 = 0;
в) 6x2 – y2 – 36x + 12y – 48 = 0; г) y2 + 2x – 4y – 2 = 0.
№21. а) x2 + y2 – 10x + 4y + 4 = 0; б) 4x2 + 25y2 – 24x + 350y + 57 = 0;
в) 2x2 – 6y2 + 12x – 12y = 0; г)  .
.
№22. а) x2 + y2 + 4x – 60 = 0; б) 2x2 + 5y2 – 12x – 10y + 9 = 0;
в) x2 – 16y2 – 4x + 32y – 28 = 0; г) 2y2 – x – 12y + 14 = 0.
№23. а) x2 + y2 – 10x + 4y + 29 = 0; б) x2 + 4y2 + 4x – 16y – 18 = 0;
в) 2x2 – y2 – 8x – 2y – 1 = 0; г) 4x2 – 8x – y – 7 = 0.
№24. а) x2 + y2 – 4x + 2y + 1 = 0; б) 4x2 + 9y2 + 8x – 18y – 23 = 0;
в) – 2x2 + 4y2 + 4x + 8y – 6 = 0; г) y2 – x – 2y + 2 = 0.
№25. а) x2 + y2 + 6x – 4y + 4 = 0; б) 4x2 – 16y2 – 8x – 64y – 76 = 0;
в) 3x2 + 6y2 + 6x + 36y + 6 = 0; г) x2 + y + 2x – 8 = 0.
№26. а) x2 + y2 + 8x = 0; б) 2x2 + 3y2 – 12x + 18y + 39 = 0;
в) 6x2 – 4y2 + 12x – 18 = 0; г) 2x2 + 16x + y + 24 = 0.
№27. а) x2 +y2 – 2x – 2y – 14 = 0; б) 5x2 + 6y2 + 20x + 12y – 4 = 0;
в) – 2x2 + 4y2 + 12x – 14y – 6 = 0; г) y2 + x – 2y + 2 = 0.
№28. а) x2 + y2 + 10x – 8y + 25 = 0; б) 2x2 – 5y2 + 16x + 10y + 17 = 0;
в) 3x2 + 2y2 + 6x + 12y + 15 = 0; г) – y2 + x + 2y – 3 = 0.
№29. а) x2 + y2 – 2x + 8y + 8 = 0; б) 2x2 + 3y2 – 6x + 24y + 44 = 0;
в) – 6x2 + 8y2 + 12x + 64y – 20 = 0; г) x2 + 8x – 4y + 20 = 0.
№30. а) x2 + y2 + 6x – 2y + 6 = 0; б) 4x2 + 5y2 – 16x – 20y + 16 = 0;
в) 3x2 – 9y2 – 6x – 12 = 0; г) y2 + x + 2y – 4 = 0.
Индивидуальные задания № 4
(Глава 4. Введение в математический анализ. Предел функции. Непрерывность функции)
ЗАДАНИЕ 1. Найти указанные пределы
№1.  ; а) х0 = 2; б) х0 = - 1; в) х0 = ¥.
; а) х0 = 2; б) х0 = - 1; в) х0 = ¥.
№2. 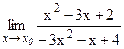 ; а) х0 = - 1; б) х0 = 1; в) х0 = ¥.
; а) х0 = - 1; б) х0 = 1; в) х0 = ¥.
№3.  ; а) х0 = 2; б) х0 = - 2; в) х0 = ¥.
; а) х0 = 2; б) х0 = - 2; в) х0 = ¥.
№4.  ; а) х0 = 1; б) х0 = 2; в) х0 = ¥.
; а) х0 = 1; б) х0 = 2; в) х0 = ¥.
№5.  ; а) х0 = - 2; б) х0 = - 1; в) х0 = ¥.
; а) х0 = - 2; б) х0 = - 1; в) х0 = ¥.
№6.  ; а) х0 = - 1; б) х0 = 1; в) х0 = ¥.
; а) х0 = - 1; б) х0 = 1; в) х0 = ¥.
№7.  ; а) х0 = 2; б) х0 = - 2; в) х0 = ¥.
; а) х0 = 2; б) х0 = - 2; в) х0 = ¥.
№8.  ; а) х0 = 1; б) х0 = 2; в) х0 = ¥.
; а) х0 = 1; б) х0 = 2; в) х0 = ¥.
№9.  ; а) х0 = - 2; б) х0 = - 1; в) х0 = ¥.
; а) х0 = - 2; б) х0 = - 1; в) х0 = ¥.
№10.  ; а) х0 = - 1; б) х0 = 1; в) х0 = ¥.
; а) х0 = - 1; б) х0 = 1; в) х0 = ¥.
№11.  ; а) х0 = 2; б) х0 = - 2; в) х0 = ¥.
; а) х0 = 2; б) х0 = - 2; в) х0 = ¥.
№12.  ; а) х0 = 1; б) х0 = 2; в) х0 = ¥.
; а) х0 = 1; б) х0 = 2; в) х0 = ¥.
№13.  ; а) х0 = - 2; б) х0 = - 1; в) х0 = ¥.
; а) х0 = - 2; б) х0 = - 1; в) х0 = ¥.
№14.  ; а) х0 = - 1; б) х0 = 1; в) х0 = ¥.
; а) х0 = - 1; б) х0 = 1; в) х0 = ¥.
№15.  ; а) х0 = 2; б) х0 = - 2; в) х0 = ¥.
; а) х0 = 2; б) х0 = - 2; в) х0 = ¥.
№16.  ; а) х0 = 1; б) х0 = 2; в) х0 = ¥.
; а) х0 = 1; б) х0 = 2; в) х0 = ¥.
№17. 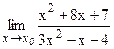 ; а) х0 = - 2; б) х0 = - 1; в) х0 = ¥.
; а) х0 = - 2; б) х0 = - 1; в) х0 = ¥.
№18.  ; а) х0 = - 1; б) х0 = 1; в) х0 = ¥.
; а) х0 = - 1; б) х0 = 1; в) х0 = ¥.
№19.  ; а) х0 = 2; б) х0 = - 2; в) х0 = ¥.
; а) х0 = 2; б) х0 = - 2; в) х0 = ¥.
№20.  ; а) х0 = 1; б) х0 = 2; в) х0 = ¥.
; а) х0 = 1; б) х0 = 2; в) х0 = ¥.
№21.  ; а) х0 = 1; б) х0 = - 1; в) х0 = ¥.
; а) х0 = 1; б) х0 = - 1; в) х0 = ¥.
№22.  ; а) х0 = 2; б) х0 = 3; в) х0 = ¥.
; а) х0 = 2; б) х0 = 3; в) х0 = ¥.
№23.  ; а) х0 = 3; б) х0 = - 3; в) х0 = ¥.
; а) х0 = 3; б) х0 = - 3; в) х0 = ¥.
№24.  ; а) х0 = - 3; б) х0 = - 2; в) х0 = ¥.
; а) х0 = - 3; б) х0 = - 2; в) х0 = ¥.
№25.  ; а) х0 = 2; б) х0 = 4; в) х0 = ¥.
; а) х0 = 2; б) х0 = 4; в) х0 = ¥.
№26.  ; а) х0 = 1; б) х0 = 2; в) х0 = ¥.
; а) х0 = 1; б) х0 = 2; в) х0 = ¥.
№27.  ; а) х0 = 0; б) х0 = - 5; в) х0 = ¥.
; а) х0 = 0; б) х0 = - 5; в) х0 = ¥.
№28.  ; а) х0 = 2; б) х0 = - 1; в) х0 = ¥.
; а) х0 = 2; б) х0 = - 1; в) х0 = ¥.
№29. 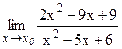 ; а) х0 = 1; б) х0 = 3; в) х0 = ¥.
; а) х0 = 1; б) х0 = 3; в) х0 = ¥.
№30.  ; а) х0 = - 1; б) х0 = 4; в) х0 = ¥.
; а) х0 = - 1; б) х0 = 4; в) х0 = ¥.
ЗАДАНИЕ 2. Найти указанные пределы
№1. 
№2. 
№3. 
№4. 
№5. 
№6. 
№7. 
№8. 
№9. 
№10. 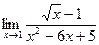
№11. 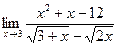
№12. 
№13. 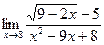
№14. 
№15. 
№16. 
№17. 
№18. 
№19. 
№20. 
№21. 
№22. 
№23. 
№24. 
№25. 
№26. 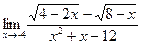
№27. 
№28. 
№29. 
№30. 
ЗАДАНИЕ 3. Найти указанные пределы
Вычислить пределы функций, используя первый замечательный предел.
№1. 
№2. 
№3. 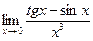
№4. 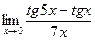
№5. 
№6. 
№7. 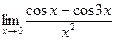
№8. 
№9. 
№10. 
№11. 
№12. 
№13. 
№14. 
№15. 
№16. 
№17. 
№18. 
№19. 
№20. 
№21. 
№22. 
№23. 
№24. 
№25. 
№26. 
№27. 
№28. 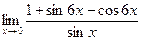
№29. 
№30. 
№31. 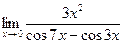
№32. 
ЗАДАНИЕ 4. Вычислить пределы функций, используя второй замечательный предел.
№1. 
№2. 
№3. 
№4. 
№5. 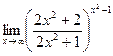
№6. 
№7. 
№8. 
№9. 
№10. 
№11. 
№12. 
№13. 
№14. 
№15. 
№16. 
№17. 
№18. 
№19. 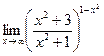
№20. 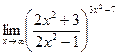
№21. 
№22. 
№23. 
№24. 
№25. 
№26. 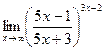
№27. 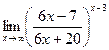
№28. 
№29. 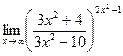
№30. 
№31. 
ЗАДАНИЕ 5. Вычислить пределы функций с помощью эквивалентных бесконечно малых.
№1. 
№2. 
№3. 
№4. 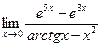
№5. 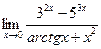
№6. 
№7. 
№8. 
№9. 
№10. 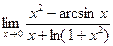
№11. 
№12. 
№13. 
№14. 
№15. 
№16. 
№17. 
№18. 
№19. 
№20. 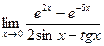
№21. 
№22. 
№23. 
№24. 
№25. 
№26. 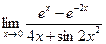
№27. 
№28. 
№29. 
№30. 
№31. 
№32. 
ЗАДАНИЕ 6. Найти точки разрыва функции и определить характер точек разрыва. Сделать схематический чертеж.
№1. 
№2. 
№3. 
№4. 
№5. 
№6. 
№7. 
№8. 
№9. 
№10. 
№11. 
№12. 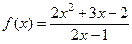
№13. 
№14. 
№15. 
№16. 
№17. 
№18. 
№19. 
№20. 
№21. 
№22. 
№23. 
№24. 
№25. 
№26. 
№27. 
№28. 
№29. 
№30. 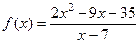
ЗАДАНИЕ 7. Функция задается различными аналитическими выражениями для различных областей изменения независимой переменной. Найти точки разрыва функции, если они существуют. Сделать схематический чертеж.
№1. 
№2. 
№3. 
№4. 
№5. 
№6. 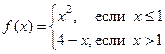
№7. 
№8. 
№9. 
№10. 
№11. 
№12. 
№13. 
№14. 
№15. 
№16. 
№17. 
№18. 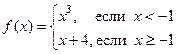
№19. 
№20. 
№21. 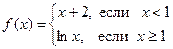
№22. 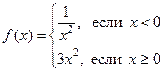
№23. 
№24. 
№25. 
№26. 
№27. 
№28. 
№29. 
№30. 
ЗАДАНИЕ 8. Найти точки разрыва функции и определить их характер. Сделать схематический чертеж.
№1. 
№2. 
№3. 
№4. 
№5. 
№6. 
№7. 
№8. 
№9. 
№10. 
№11. 
№12. 
№13. 
№14. 
№15. 
№16. 
№17. 
№18. 
№19. 
№20. 
№21. 
№22. 
№23. 
№24. 
№25. 
№26. 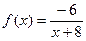
№27. 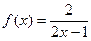
№28. 
№29. 
№30. 