Примерные задачи
«Основы финансовых вычислений»
Задача 1. Банк выдал ссуду размером 5000000 рублей. Дата выдачи ссуды – 20 июня 2013 г., возврата – 15 сентября 2013 г. День выдачи и день возврата считать за один день. Проценты рассчитываются по простой процентной ставке 15% годовых.
Найти:
1) точные проценты с точным числом дней ссуды;
2) обыкновенные проценты с точным числом дней ссуды;
3) обыкновенные проценты с приближенным числом дней ссуды.
Задача 2. Банк выдал ссуду размером 4000000 рублей. Дата выдачи ссуды – 10 июня 2013 г., возврата – 18 сентября 2013 г. День выдачи и день возврата считать за один день. Проценты рассчитываются по простой процентной ставке 20% годовых.
Найти:
1) точные проценты с точным числом дней ссуды;
2) обыкновенные проценты с точным числом дней ссуды;
3) обыкновенные проценты с приближенным числом дней ссуды.
Задача 3. Кредитный договор заключен на 1 год. Первоначальная сумма равна 2000000 руб. Период начисления процентов –квартал. Определить наращенную сумму и множитель наращения для случаев:
1) применяется сложная ставка процентов, за первый квартал – 10 %, а за каждый последующий квартал на 1 % меньше;
2) применяется простая ставка процентов, за первый квартал – 10 %, а за каждый последующий квартал на 1 % меньше;
3) применяется сложная ставка – 10 %, одинаковая для всех кварталов;
4) применяется простая ставка – 10 %, одинаковая для всех кварталов.
Задача 4. Кредитный договор заключен на 1 год. Первоначальная сумма равна 3000000 руб. Период начисления процентов –квартал. Определить наращенную сумму и множитель наращения для случаев:
1) применяется сложная ставка процентов, за первый квартал – 10 %, а за каждый последующий квартал на 1 % меньше;
2) применяется простая ставка процентов, за первый квартал – 10 %, а за каждый последующий квартал на 1 % меньше;
3) применяется сложная ставка – 10 %, одинаковая для всех кварталов;
4) применяется простая ставка – 10 %, одинаковая для всех кварталов.
Задача 5. Кредитный договор заключен на 1 год. Первоначальная сумма равна 5000000 руб. Проценты начисляются 2 раза в году и капитализируются. Наращенная сумма через год составила 8450000 руб.
Определить номинальную процентную ставку. Какова была бы наращенная сумма, эффективная ставка и множитель наращения, если бы начисление процентов производилось ежемесячно при прочих неизменных условиях договора.
Задача 6. Кредитный договор заключен на 1 год. Первоначальная сумма равна 2500000 руб. Проценты начисляются 2 раза в году и капитализируются. Наращенная сумма через год составила 4225000 руб.
Определить номинальную процентную ставку. Какова была бы наращенная сумма, эффективная ставка и множитель наращения, если бы начисление процентов производилось ежеквартально при прочих неизменных условиях договора.
Задача 7. Вклад 25000 рублей положен в банк на полгода с ежемесячным начислением сложных процентов по номинальной ставке 32% годовых. Определить реальный доход вкладчика, если ожидаемый ежемесячный уровень инфляции составит 6%.
Задача 8. Три платежа в размере: 2000 руб. со сроком 2 года, 4000 руб. со сроком 3 года и 3000 руб. со сроком 4 года заменяются одним в размере 8000 руб. Стороны договорились об использовании сложной процентной ставки 18% годовых. Определить срок консолидированного платежа.
Задача 9. Фирма в качестве компенсации работникам за причиненный им ущерб должна выплатить 100 млн. руб. в течение 25 лет. Платежи должны производиться равномерно в течение этого периода – в конце каждого квартала. Найти реальную (современную) стоимость данной компенсации для фирмы, если принять годовую ставку сложных процентов на уровне 10%.
Задача 10. Кредит в сумме 200 млн. руб. выдан на 4 года по ставке сложных процентов 20 % годовых. Возврат кредита предполагается осуществлять в конце каждого квартала равными выплатами, включающими сумму основного долга и проценты. Найти величину погасительного платежа за квартал.
Задача 11. Ссуда в размере 100000 руб. выдана 1 февраля до 1 августа включительно под простые проценты 15 % годовых. В счет погашения долга 16 апреля поступило 60000 руб., 16 июня – 1000 руб.
Определить остаток долга на конец срока актуарным методом и методом расчета по правилу торговца.
Задача 12. Банк объявил следующие условия выдачи ссуды на год: за первый квартал ссудный процент 20%, а в каждом последующем квартале процентная ставка по ссуде увеличивается на 5%. Определить сумму к возврату в банк, если ссуда выдана на год и составляет 35000 рублей (проценты простые).
Задача 13. В фонд поступают средства, на которые начисляются проценты по ставке 12% годовых, причем выплаты производятся в конце каждого квартала, а проценты начисляются ежемесячно. Годовая выплата 12000 рублей. За какой срок величина фонда составит 120000 рублей?
Задача 14. В течение 5 лет на расчетный счет в конце каждого года поступает по 5000 рублей, на которые начисляются проценты по сложной годовой ставке 20%. Требуется определить:
1) сумму на расчетном счете к концу указанного срока;
2) современную стоимость потока платежей.
Какой срок потребуется для образования той же суммы фонда, если проценты будут начисляться ежеквартально.
Задача 15. Через 5 лет должник выплатит кредитору сумму в размере 1000000 руб.
1) Какова первоначальная сумма, полученная должником если кредит выдан:
а) под 20 % годовых, проценты простые;
б) под 20 % годовых, проценты сложные.
2) Какую сумму получит за это обязательство кредитор, если он переуступит обязательство банку, который учтет его:
а) по простой учетной ставке 20 % годовых;
б) по сложной учетной ставке 20 % годовых.
Задача 16. Через 3 года должник выплатит кредитору сумму в размере 1000000 руб.
1) Какова первоначальная сумма, полученная должником если кредит выдан:
а) под 15 % годовых, проценты простые;
б) под 15 % годовых, проценты сложные.
2) Какую сумму получит за это обязательство кредитор, если он переуступит обязательство банку, который учтет его:
а) по простой учетной ставке 15 % годовых;
б) по сложной учетной ставке 15 % годовых.
Задача 17. В течение 10 лет на расчетный счет в конце каждого года поступает по 10000 рублей, на которые начисляются проценты по сложной годовой ставке 15%. Требуется определить:
1) сумму на расчетном счете к концу указанного срока;
2) современную стоимость потока платежей.
Какой срок потребуется для образования той же суммы фонда, если проценты будут начисляться ежеквартально.
Задача 18. В течение 5 лет в конце каждого полугодия на расчетный счет поступают равными долями платежи из расчета 8 000000 руб. в год, на которые ежеквартально начисляются проценты из расчета 20 % годовых. Требуется определить сумму на расчетном счете к концу указанного срока. Найти размер платежей, при которых эта же сумма на расчетном счете образуется за 4 года.
Задача 19. В течение 10 лет в конце каждого месяца на расчетный счет поступают равными долями платежи из расчета 4 000000 руб. в год, на которые ежемесячно начисляются проценты из расчета 18,5 % годовых. Требуется определить сумму на расчетном счете к концу указанного срока.
Задача 20. В фонд ежегодно в конце периода поступают средства в течение 5 лет, на которые начисляются проценты по ставке 12% годовых, причем выплаты производятся в конце каждого квартала, а проценты начисляются ежемесячно (раз в году). Наращенная сумма к концу срока составит 100000 рублей. Определить коэффициент наращения ренты и размер годовой выплаты.
Задача 21. Фирма в качестве компенсации работникам за причиненный им ущерб должна выплатить 100 млн. руб. в течение 20 лет. Платежи должны производиться равномерно в течение этого периода – в конце каждого квартала. Найти реальную (современную) стоимость данной компенсации для фирмы, если принять годовую ставку сложных процентов на уровне 12%.
Задача 22. Кредит в сумме 100 млн. руб. выдан на 3 года по ставке сложных процентов 20 % годовых. Возврат кредита предполагается осуществлять в конце каждого квартала равными выплатами, включающими сумму основного долга и проценты. Найти величину погасительного платежа за квартал.
Задача 23. Через 4 года должник выплатит кредитору сумму в размере 600000 руб.
1) Какова первоначальная сумма, полученная должником если кредит выдан:
а) под 20 % годовых, проценты простые;
б) под 20 % годовых, проценты сложные.
2) Какую сумму получит за это обязательство кредитор, если он переуступит обязательство банку, который учтет его:
а) по простой учетной ставке 20 % годовых;
б) по сложной учетной ставке 20 % годовых.
Задача 24. Доходности финансового проекта за два последовательных периода времени 
равны соответственно 10 и 15%. Определите доходность 
за период 
. На какую величину доходность за два периода отличается от суммы доходностей?
Задача 25. Рассматриваются два альтернативных проекта А и В. В таблице представлены доходности проектов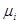 
и соответствующие им вероятности 
.
Оценив рискованность проектов и их ожидаемую доходность, необходимо выбрать наиболее привлекательный проект.
| Усл. бозн. | А | В | ||||||||
|
| 0,1 | 0,3 | 0,3 | 0,2 | 0,1 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 |
| , %
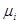| 3,2 | 4,5 | 6,2 | 8,0 | 10,5 | 4,5 | 5,2 | 8,5 | 10,3 | 11,7 |
Задача 26. Рассматриваются два альтернативных проекта А и В. В таблице представлены доходности проектов 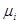и соответствующие им вероятности .
Оценив рискованность проектов и их ожидаемую доходность, необходимо выбрать наиболее привлекательный проект.
| Усл. бозн. | А | В | ||||||||
|
| 0,1 | 0,3 | 0,3 | 0,2 | 0,1 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 |
| , %
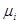| 4,5 | 5,2 | 8,5 | 10,3 | 11,7 | 3,2 | 4,5 | 6,2 | 8,0 | 10,5 |
Задача 27. Дана матрица последствий Q, в которой строки – возможные управленческие решения, а столбцы – исходы, соответствующие альтернативным вариантам реальной ситуации (состояниям внешней среды).
Необходимо выбрать рациональную управленческую стратегию в ситуации неопределенности и риска, применяя критерии Вальда, максимакса, Сэвиджа, Гурвица, приняв рекомендуемое для критерия Гурвица значение 
.
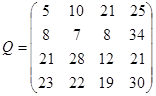; =0,35
Задача 28. Дана матрица последствий Q, в которой строки – возможные управленческие решения, а столбцы – исходы, соответствующие альтернативным вариантам реальной ситуации (состояниям внешней среды).
Необходимо выбрать рациональную управленческую стратегию в ситуации неопределенности и риска, применяя критерии Вальда, максимакса, Сэвиджа, Гурвица, приняв рекомендуемое для критерия Гурвица значение .
; =0,55
Задача 29. Дана матрица последствий. Найти множество решений, оптимальных по Парето.
| В1 | В2 | В3 | В4 | В5 | |
| A1 | |||||
| A2 | |||||
| A3 | |||||
| A4 | |||||
| A5 | |||||
| A6 | |||||
| A7 | |||||
| A8 | |||||
| A9 |
Задача 30. Дана матрица последствий. Найти множество решений, оптимальных по Парето.
| В1 | В2 | В3 | В4 | В5 | |
| A1 | |||||
| A2 | |||||
| A3 | |||||
| А4 | |||||
| A5 | |||||
| A6 | |||||
| A7 | |||||
| А8 | |||||
| A9 |
Задача 31. Пусть портфель состоит из двух независимых бумаг с доходностями и рисками соответственно (0,1;0.5) и (0.4;0,9). Найти портфель минимального риска, его риск и доходность.
Задача 32. Пусть портфель состоит из трех независимых бумаг с доходностями и рисками соответственно (0,1;0.5), (0.2;0.7) и (0.4;0,9). Найти портфель минимального риска, его риск и доходность.
Задача 33. Необходимо сформировать оптимальный портфель Марковица из трех некоррелированных ценных бумаг с эффективностями и рисками: (6,20), (12,50), (42, 80). Нижняя граница доходности портфеля задана равной 17.
Задача 34. Сформировать портфель Тобина минимального риска из двух видов ценных бумаг: безрисковой с эффективностью 2 и рисковой с эффективностью 10 и риском 5. Доходность портфеля равна 8.
Задача 35. Портфель наполовину (по стоимости) состоит из бумаг первого вида с доходностью 15% годовых и из бумаг второго вида с доходностью 7% годовых. Какова эффективность портфеля?
Задача 36. Дан портфель из двух бумаг с доходностью и риском соответственно (0,4;0.7) и (0.6;0.9). Найти портфель нулевого риска и его доходность для случая полной антикорреляции.
Задача 37. Найти текущую стоимость облигации номинальной стоимостью 800 ден. ед., сроком погашения 4 года и ежегодными выплатами по купонной ставке 12% при годовой процентной ставке 18%.
Задача 38. Курс облигации равен 95, купонный доход 12%. Найти текущую доходность облигации.
Задача 39. Курс облигации равен 1.1, купонный доход 12%. Найти текущую доходность облигации. Найти доходность к погашению через 20 лет.
Задача 40. Дюрация облигации равна D=10. Известно, что ее доходность к погашению увеличилась с 12 до 13.5%. Определить на сколько процентов изменилась цена облигации.