Лабораторная работа N 4
Исследование характеристик системы обслуживания М/М/1
Цель работы
Приобретение практических навыков исследования основных характеристик локальных систем с помощью модели М/М/1.
Темы для предварительного изучения
1. Введение в теорию очередей.
2. Пуассоновский процесс и его основные характеристики.
3. Система обслуживания М/М/1.
Постановка задачи
Ознакомиться с основными характеристиками системы обслуживания М/М/1 и исследовать влияние:
· скорости поступления заявок на входе системы;
· скорости обслуживания заявок в системе;
· емкости накопителя системы.
Краткие теоретические сведения
М/М/1 — система с одной обслуживающей линией, пуассоновским входящим потоком, показательным распределением времени обслуживания и дисциплиной ОПП (обслуживается первый поступивший). Обозначение М/М/1 предложено британским статистиком Д. Дж. Кендаллом. В общем виде обозначение Кендалла для системы обслуживания имеет вид А/В/С, где символ А обозначает распределение на входе, В — распределение времени обслуживания, а С — число обслуживаемых линий. В частности, для обозначения пуассоновского процесса или эквивалентного ему показательного распределения применяется символ М (Марковский процесс). Таким образом, система обслуживания типа М/М/m характеризуется пуассоновским входящим потоком, показательным распределением времени обслуживания и числом обслуживающих линий m. Система M/G/1 характеризуется пуассоновским входящим потоком, произвольным распределением времени обслуживания (от слова general) и одной обслуживающей линией. В частном случае, М/D/l обозначает систему с фиксированным (детерминированным), или постоянным, временем обслуживания.
Статистические свойства системы М/М/1, например среднее время занятия, вероятность блокировки для конечной очереди, средняя пропускная способность и т. п., легко могут быть определены, если найдены вероятности рn состояний системы. По определению рn — это вероятность того, что в системе находятся п клиентов (пакетов или вызовов), включая клиента, находящегося на обслуживании. Предполагается, что система работает в установившемся режиме, и поэтому указанные вероятности не изменяются во времени. Можно ожидать, что со временем эти вероятности приближаются к установившимся, стационарным, неизменным во времени значениям, начиная от некоторых определенных исходных значений: (например, из состояния пустой системы), если входящий поток и распределение времени обслуживания инвариантны во времени. Ниже мы покажем, что эти стационарные вероятности легко определяются на основании простого предположения о равновесии. Сейчас же мы воспользуемся более общим предположением о зависимости процесса от времени.
Конкретно, предположим, что входящий поток в однолинейную систему обслуживания — пуассоновский с параметром λ. Пусть процесс обслуживания (длина пакета или продолжительность, соединения) описывается показательным распределением с параметром μ. Тогда вероятность pn(t +Δt) того, что в момент (t+Δt) в системе будут находиться п клиентов (пакетов или вызовов) легко может быть получена в виде функции соответствующих вероятностей в момент времени t. Из диаграммы изменения состояний во времени очевидно, что если система в момент t + Δt находится в состоянии п, то в момент t она могла находиться только в состоянии п— 1, п или п+ 1 (предполагая ради простоты, что n >1). Вероятность pn(t+Δt) того, что в момент времени t + Δ t система находится в состоянии п, должна быть суммой (взаимно исключающих) вероятностей состояний п —1, п или п + 1, в которых система могла быть в момент t, помноженных соответственно на (независимые) вероятности поступления в состояние п, происходящего за Δ t единиц времени. Таким образом, мы получим

+  (2.1)
(2.1)
Вероятности перехода из одного состояния в другое получены в результате рассмотрения путей, по которым происходят эти переходы, и расчета соответствующих вероятностей с использованием свойств поступающего потока и распределения времени обслуживания. Например, если система осталась в состоянии п, п  1, то могли произойти либо один уход и одно поступление с вероятностью
1, то могли произойти либо один уход и одно поступление с вероятностью  , либо ни одного ухода или поступления с вероятностью (1-
, либо ни одного ухода или поступления с вероятностью (1-  )(1-
)(1-  ), что и показано в первой строке. Аналогично получаются и другие члены равенства (2.1).
), что и показано в первой строке. Аналогично получаются и другие члены равенства (2.1).
Поскольку о( t) включает члены порядка (
t) включает члены порядка (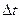 )2 и выше, члены равенства (2.1), в которые входит (
)2 и выше, члены равенства (2.1), в которые входит (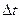 )2, включаются в состав o(
)2, включаются в состав o( t). (Они сохранены и показаны в явном виде, чтобы помочь понять равенство (2.1).) Производя упрощение и объединяя вместе члены о (
t). (Они сохранены и показаны в явном виде, чтобы помочь понять равенство (2.1).) Производя упрощение и объединяя вместе члены о ( t), найдем
t), найдем  (2.2)
(2.2)
Равенство (2.2) может быть использовано для исследования переходного (зависящего от времени) режима работы системы М/М/1, при условии, что эта работа начинается в момент времени t=0 с некоторого известного состояния или набора состояний. Иначе, путем разложения pn(t+Δt) в ряд Тейлора относительно t с сохранением лишь первых двух членов можно найти дифференциально-разностное уравнение, описывающее изменение pn(t) во времени
 (2.3)
(2.3)
Используя (2.2) и (2.3) и проведя упрощения, легко получить следующее уравнение
 (2.4)
(2.4)
Это — дифференциально-разностное уравнение, решая которое можно получить зависимость pn(t) в явном виде.
Как было установлено ранее, вероятность pn(t) должна приближаться к постоянному стационарному значению рn с увеличением времени. Предполагая, что это имеет место (позднее будет показано, что в случае бесконечной очереди это гарантируется при условии λ<μ.), мы должны при стационарном значении рп иметь  /dt = 0. Тогда уравнение (2.4) для случая стационарных, неизменных во времена вероятностей, упрощается и принимает для системы М/М/1 вид
/dt = 0. Тогда уравнение (2.4) для случая стационарных, неизменных во времена вероятностей, упрощается и принимает для системы М/М/1 вид
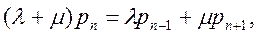 n>1. (2.5)
n>1. (2.5)
Этому уравнению может быть дана физическая интерпретация, позволяющая записать его непосредственно, минуя долгий процесс его вывода из (2.1). Более важно, используя описываемый ниже подход, мы сможем выписывать далее подобные уравнения для более общих случаев систем обслуживания, зависящих от состояний.

Рис. 2.1. Диаграмма состояний системы М/М/1
Рассмотрим диаграмму состояний (рис. 2.1), на которой показана система М/М/1. Ввиду предположений о пуассоновском процессе поступления и ухода клиентов, переходы имеют место только между соседними состояниями с показательными интенсивностями. С интенсивностью λпроисходит переход на одно состояние вправо при поступлении клиента в систему, а с интенсивностью μ— переход па одно состояние влево при завершении обслуживания или уходе клиента. Иначе говоря, если эти интенсивности умножить на Δ t, получится вероятность λΔ t перехода на одно состояние вправо за счет поступления или вероятность μΔt перехода на одно состояние влево за счет завершения обслуживания (ухода). (Если система находится в состоянии 0, т. е. свободна, она может перейти только вправо в состояние 1 за счет поступления клиента.)
Форма уравнения (2.5) показывает, что при работе системы действует стационарный принцип равновесия. Левая часть уравнения (2.5) описывает интенсивность уходов и з состояния п, если задано, что система находится в состоянии п с вероятностью рп. Правая сторона описывает интенсивность приходов в состояние п из состояний п —1 или п +1. Чтобы существовали вероятности стационарного состояния, эти две интенсивности должны быть равны.
Уравнения равновесия играют ключевую роль в исследовании сиг-тем обслуживания. Уравнение (2.5) для вероятностей состояний может быть решено несколькими способами. При простейшем из них может быть опять-таки использовано условие равновесия. Рассмотрим рисунок 2.2, на котором диаграмма состояний системы М/М/1 перерисована с рис. 2.1 с указанием двух замкнутых областей 1 и 2. Если рассчитать общин «поток вероятности», пересекающий границу области 1, и приравнять исходящий поток (интенсивность уходов из состояния п) входящему потоку (интенсивность прихода в состояние п), получится уравнение (2.5).
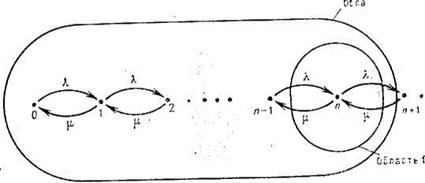
Рис. 2.11. Равновесие потоков в системе М/М/1
Обратимся теперь к области 2, которая охватывает все множество точек от 0 до п. Поток, поступающий в эту область, равен  , а поток, покидающий ее, равен λ рп. Приравнивая эти два потока, получим
, а поток, покидающий ее, равен λ рп. Приравнивая эти два потока, получим
λ рп=  . (2.6)
. (2.6)
Читателю предлагается показать, что это простое уравнение равновесия фактически удовлетворяет уравнению (2.5). Интуитивная идея о равновесии интенсивностей ухода из некоторого состояния и прихода в это состояние не только дает возможность записать уравнение равновесия (2.5), но также и получить его решение! Повторяя уравнение (2.6) п раз, очень просто находим, что равновесия (2.5), но также и получить его решение! Повторяя уравнение (2.6) п раз, очень просто находим, что
pn = 
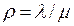 . (2.7)
. (2.7)
Для того чтобы найти оставшуюся неизвестной вероятность po, теперь необходимо обратиться к нормирующему условию для вероятностей
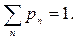
Для случая бесконечной очереди типа М/М/1 очень просто находится рo = (1 —  ), если
), если  < 1, что приводит к решению для установившегося режима в виде
< 1, что приводит к решению для установившегося режима в виде
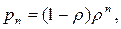
 (2.8)
(2.8)
Заметим, что необходимое условие  уже упоминалось ранее. Его значение опять-таки состоит в том, что для существования равновесия интенсивность поступлений, или нагрузка системы, должна быть меньше ее п ропускной способности μ.. Если это условие для данной модели с бесконечной очередью нарушается, равновесие никогда не будет достигнуто. Математически факт существования равновесия только при ρ < 1 отмечается при рассмотрении предельного случая ρ = 1. Поскольку ро = 1 — ρ, то ро = 0. Но из уравнения (2.6) следует p1=ρpo=0, p2=0, и т. д. Таким образом, все стационарные вероятности равны нулю и, следовательно, равновесия не существует. Распределение вероятностей состояний (2.8) системы М/М/1 называется геометрическим распределением. Заметим, что поскольку вероятность свободности системы ρо = 1 — ρ, то вероятность того, что система непуста, в точности равна ρ, т. е. коэффициенту использования системы.
уже упоминалось ранее. Его значение опять-таки состоит в том, что для существования равновесия интенсивность поступлений, или нагрузка системы, должна быть меньше ее п ропускной способности μ.. Если это условие для данной модели с бесконечной очередью нарушается, равновесие никогда не будет достигнуто. Математически факт существования равновесия только при ρ < 1 отмечается при рассмотрении предельного случая ρ = 1. Поскольку ро = 1 — ρ, то ро = 0. Но из уравнения (2.6) следует p1=ρpo=0, p2=0, и т. д. Таким образом, все стационарные вероятности равны нулю и, следовательно, равновесия не существует. Распределение вероятностей состояний (2.8) системы М/М/1 называется геометрическим распределением. Заметим, что поскольку вероятность свободности системы ρо = 1 — ρ, то вероятность того, что система непуста, в точности равна ρ, т. е. коэффициенту использования системы.
Рассмотрим теперь обобщение данного анализа на случай конечной очереди, вмещающей не более N пакетов. Легко видеть, что основное уравнение равновесия (2.5) неизменно, кроме двух граничных точек п = 0 и n = N. Равенство (2.7) является решением и для них. Единственным различием здесь является то, что вероятность ро того, что система свободна, изменяется в зависимости от нормирующего условия, в котором суммирование производится по всему конечному числу состояний

Читателю остается показать, что в этом случае
 (2.9)
(2.9)
И, следовательно, для конечной очереди в системе М/М/1
 (2.10)
(2.10)
В частности, вероятность того, что очередь заполнена, равна
 (2.11)
(2.11)
Но этавероятность должна быть такой же, как и вероятность блокировки, т. е. вероятность того, что клиенты (пакеты или вызовы) не могут быть приняты системой. Это можно проиллюстрировать следующим простым рассуждением, которое в дальнейшем окажется полезным при анализе некоторых характеристик сетей передачи данных. Рассмотрим систему, представленную на рис. 2.1. Это не обязательно система М/М/1 с конечной очередью. Она может быть любой системой, которая блокирует клиентов при их поступлении. На рисунке показана нагрузка λ, определяемая как среднее число поступлений в секунду. При вероятности блокировки Рв чистая интенсивность поступлений равна λ(1 — Рв). Но это должно быть ни чем иным, как пропускной способностью γ или числом клиентов, обслуживаемых за секунду в консервативной системе. Таким образом, имеем
 (2.12)
(2.12)
Вместе с тем можно рассчитать пропускную способность другим путем, обратившись к выходу системы. В частности, для однолинейной системы, о которой идет речь, средняя скорость обслуживания равна μ клиентов/с, если система всегда непуста. Но поскольку система иногда бывает свободной (с вероятностью ро), фактическая скорость обслуживания, или производительность γ, меньше, чем μ. Более точно, 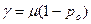 , так как (1— Ро)~ вероятность того, что система непуста (пока в системе имеется, по крайней мере, один клиент, средняя скорость обслуживания будет равна μ). Таким образом. (1 - ро) — это коэффициент использования (однолинейной системы). Для проверки рассмотрим бесконечную очередь в системе М/М/1. В этом случае не возникает блокировок, и производительность
, так как (1— Ро)~ вероятность того, что система непуста (пока в системе имеется, по крайней мере, один клиент, средняя скорость обслуживания будет равна μ). Таким образом. (1 - ро) — это коэффициент использования (однолинейной системы). Для проверки рассмотрим бесконечную очередь в системе М/М/1. В этом случае не возникает блокировок, и производительность  , т. е. средней скорости поступлении. Таким образом, мы должны получить
, т. е. средней скорости поступлении. Таким образом, мы должны получить  , или
, или 
 в точности, что и было найдено ранее! В случае системы М/М/1 с конечной очередью мы приравниваем чистую скорость поступления
в точности, что и было найдено ранее! В случае системы М/М/1 с конечной очередью мы приравниваем чистую скорость поступления  средней скорости уходов
средней скорости уходов 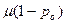 и получаем
и получаем
γ=  =
= 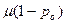 . (2.13)
. (2.13)
Читателю остается показать, подставив в (2.13) результат (2.9), что в конечной системе М/М/1 вероятность блокировки фактически равна
 (2.14)
(2.14)
Это выражение для вероятности блокировки может быть использовано в простых расчетах при проектировании. Например, требуется узнать, какой должна быть длина очереди N, чтобы обеспечивалось заданное значение вероятности блокировки. В соответствии с (2.14) она зависит от ρ. При небольших значениях вероятности блокировки выражение (2.14) можно упростить. При ρ < 1 и N > 1 получим
 (2.15)
(2.15)
Но это в точности вероятность того, что система с бесконечной очередью находится в состоянии п = N, а это показывает, что при малых  вероятность того, что конечная система находится в состоянии п = N, может быть вычислена в предположении бесконечной очереди. При
вероятность того, что конечная система находится в состоянии п = N, может быть вычислена в предположении бесконечной очереди. При  усечение бесконечной очереди в точке п = N заметно не повлияет на статистику очереди.
усечение бесконечной очереди в точке п = N заметно не повлияет на статистику очереди.
В качестве примера применения равенства (2.15) рассмотрим случай ρ = 0,5. Тогда для получения  потребуется разместить N = 9 ожидающих клиентов. Таким образом, в сети с коммутацией пакетов концентратор должен обрабатывать лишь 9 пакетов. Если желательно получить вероятность
потребуется разместить N = 9 ожидающих клиентов. Таким образом, в сети с коммутацией пакетов концентратор должен обрабатывать лишь 9 пакетов. Если желательно получить вероятность 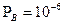 (в среднем один отказ на миллион клиентов), а р = 0,5, указанное выше число увеличивается до N =19. Увеличение ρ при росте нагрузки ведет к соответствующему увеличению N. В качестве простого примера рассмотрим концентратор в сети с коммутацией пакетов, который обрабатывает пакеты со средней, длиной 1200 бит. При наличии канала со скоростью передачи 2400 бит/с его пропускная способность составит в среднем
(в среднем один отказ на миллион клиентов), а р = 0,5, указанное выше число увеличивается до N =19. Увеличение ρ при росте нагрузки ведет к соответствующему увеличению N. В качестве простого примера рассмотрим концентратор в сети с коммутацией пакетов, который обрабатывает пакеты со средней, длиной 1200 бит. При наличии канала со скоростью передачи 2400 бит/с его пропускная способность составит в среднем 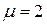 пакета/с. При ρ = 0,5 допустимой нагрузкой на концентратор будет
пакета/с. При ρ = 0,5 допустимой нагрузкой на концентратор будет 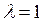 пакет/с. Следовательно, при вероятности блокировки 10-3 емкость накопителя очереди должна обеспечивать возможность размещения 9 пакетов со средней длиной 1200 бит. При
пакет/с. Следовательно, при вероятности блокировки 10-3 емкость накопителя очереди должна обеспечивать возможность размещения 9 пакетов со средней длиной 1200 бит. При  эта величина увеличивается до 19 пакетов.
эта величина увеличивается до 19 пакетов.
Возвращаясь вновь к выражению (2.10) для вероятностей системы обслуживания М/М/1 в установившемся режиме, заметим, что условия
ρ < 1 для существования стационарных вероятностей больше не требуется. Поскольку очередь конечна, указанные вероятности существуют и определяются равенством (2.10) для всех значений ρ. Отметим, в частности, что если нагрузка 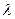 увеличивается по отношению к пропускной способности
увеличивается по отношению к пропускной способности  , то очередь переполняется все более часто, и в пределе
, то очередь переполняется все более часто, и в пределе  находится в состоянии n = N с вероятностью 1. В соответствии с (2.10)
находится в состоянии n = N с вероятностью 1. В соответствии с (2.10)  при
при  и
и 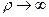 , а
, а 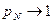 при
при 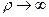 . Область ρ > 1 называется областью скученности; наиболее вероятны состояния очереди с наивысшими номерами. При
. Область ρ > 1 называется областью скученности; наиболее вероятны состояния очереди с наивысшими номерами. При 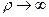 вероятность блокировки
вероятность блокировки  приближается к 1. На основании правила Лопиталя легко показать, что при ρ = 1 имеет место
приближается к 1. На основании правила Лопиталя легко показать, что при ρ = 1 имеет место  . Например, при N = 9 вероятность блокировки
. Например, при N = 9 вероятность блокировки  равна 10 -3 в случае ρ = 0,5, возрастает до 0,1 в случае ρ = 1, приблизительно равна 0,5 в случае ρ = 2 и продолжает расти до 1 при
равна 10 -3 в случае ρ = 0,5, возрастает до 0,1 в случае ρ = 1, приблизительно равна 0,5 в случае ρ = 2 и продолжает расти до 1 при 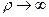 . Это говорит о том, что когда ρ находится в области скученности, система часто блокируется.
. Это говорит о том, что когда ρ находится в области скученности, система часто блокируется.
Производительность системы, которая близка к нагрузке 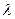 при малых ρ, в конце концов выравнивается и при возрастании ρ приближается к пропускной способности
при малых ρ, в конце концов выравнивается и при возрастании ρ приближается к пропускной способности 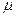 . Конкретное выражение для нормированной производительности
. Конкретное выражение для нормированной производительности 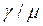 как функции нормированной нагрузки
как функции нормированной нагрузки 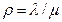 легко получить, подставляя в (2.13) результат (2.9). Это дает
легко получить, подставляя в (2.13) результат (2.9). Это дает
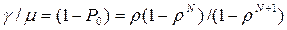 (2.16)
(2.16)
Сосредоточимся теперь па области ρ < 1, где нет скученности, для которой достаточно воспользоваться анализом бесконечного накопителя. На основании вероятностей состояний рп, которые получаются из (2.8), можно рассчитать различные статистики. Рассмотрим, в частности, среднее число Е(п) клиентов (пакетов или ожидающих вызовов) в системе, включая находящегося на обслуживании. На основании определения среднего значения случайной величины непосредственно из (2.8), произведя суммирование, получим
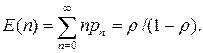 (2.17)
(2.17)
Равенство (2.17) описывает хорошо известное явление, которое все мы испытываем в повседневной жизни. Когда нагрузка системы относительно небольшая (например  ), среднее число клиентов в системе относительно мало (при ρ <0,5 оно меньше единицы). Когда же ρ увеличивается, приближаясь к 1, это среднее число резко растет за счет члена (1- ρ) в знаменателе. В реальной системе обслуживания с конечной очередью это число, очевидно, в окрестности ρ < 1 растет не так резко, но равенство (2.17) для бесконечной очереди дает неплохую модель и для конечного случая.
), среднее число клиентов в системе относительно мало (при ρ <0,5 оно меньше единицы). Когда же ρ увеличивается, приближаясь к 1, это среднее число резко растет за счет члена (1- ρ) в знаменателе. В реальной системе обслуживания с конечной очередью это число, очевидно, в окрестности ρ < 1 растет не так резко, но равенство (2.17) для бесконечной очереди дает неплохую модель и для конечного случая.
При росте нагрузки системы растет также ее производительность. Однако при этом блокируется все большее количество клиентов и, следовательно, быстро растет среднее число Е(п) клиентов в очереди. Увеличение Е(п) оборачивается увеличением времени задержки в очереди. Это типичный случай обмена в характеристиках: при увеличении нагрузки растет производительность (желательная характеристика), но одновременно возрастают блокировка и время задержки (нежелательные характеристики).
Чтобы найти общее время задержки (включающее время ожидания в очереди и, кроме того, время обслуживания или передачи), обращаются к простой формуле. Эта формула, названная по имени Литтла, который впервые ее доказал, просто говорит о том, что система обслуживания со средней скоростью поступлений λ и средним временем задержки в системе Е(Т), имеет среднюю длину очереди Е(п), которая находится из выражения
 (2.18)
(2.18)
Здесь же достаточно сказать, что это соотношение является наиболее общим и справедливо для всех систем обслуживания, включая системы с приоритетами. Параметр λинтерпретируется как интенсивность поступлений в систему. Таким образом, он соответствует нашей производительности γ. Это должно быть очевидно, поскольку клиенты, которые не попадают в систему, не могут увеличить общую задержку в системе.
Применяя формулу (2.18) к обсуждаемой системе М/М/1, с помощью (2.17) непосредственно получим
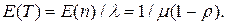 (2.19)
(2.19)
Этому выражению для среднего времени задержки в системе М/М/1 может быть дана интересная интерпретация. При ρ << 1 точное значение среднего времени обслуживания равно Е(Т)= 1/μ. Это случай (2.17), когда в очереди в среднем находится небольшое число клиентов. Поэтому на ожидание в очереди в среднем тратится очень мало времени, и задержка почти всегда объясняется лишь обслуживанием, или временем передачи. Однако при увеличении нормированной нагрузки или интенсивности трафика, обычное влияние очереди начинает ощущаться и Е(Т) быстро растет.
Очевидно, что для однолинейной системы должно выдерживаться следующее простое соотношение между средним временем ожидания E{W) и средней задержкой Е(Т) в системе:
E(T)=E(W)+1/μ. (2.20)
Теорема Литтла позволяет нам найти в явном виде соотношение для среднего числа клиентов E(q), ожидающих в очереди. Оно должно получиться в виде
E(q)=λE(W)=λE(T) - λ/μ=E(n) – ρ. (2.21)
Заметим для проверки, что в (2.21) ρ должно представлять среднее число клиентов, находящихся на обслуживании. Оно очевидно меньше единицы, поскольку на обслуживании клиент может быть, а может и не быть. Обратившись к самой обслуживающей линии, можно заметить, что если ро = 1 — ρ вероятность того, что ни один клиент не обслуживается (обслуживающая линия свободна), то вероятность того, что на обслуживании находится один клиент, равна (1 —  )=ρ. Таким образом, среднее значение точно равно ρ. Этот результат, po=1-ρ, для системы обслуживания М/М/1 может быть обобщен на любую однолинейную систему). На основании (2.21) ρ — всегда среднее число клиентов на обслуживании. Поэтому po=1-ρ всегда должно быть справедливо.
)=ρ. Таким образом, среднее значение точно равно ρ. Этот результат, po=1-ρ, для системы обслуживания М/М/1 может быть обобщен на любую однолинейную систему). На основании (2.21) ρ — всегда среднее число клиентов на обслуживании. Поэтому po=1-ρ всегда должно быть справедливо.